La devianza

In statistica la devianza è una misura della dispersione. Si ottiene calcolando la somma dei quadrati delle deviazioni dei dati di una distribuzione rispetto alla media. $$ D(x) = \sum_{i=1}^n (x_i - \mu)^2 $$

Nel caso di una distribuzione di frequenze utilizzo la formula

$$ D(x) = \sum_{i=1}^n (x_i - \mu)^2 \cdot n_i $$

Dove n è la frequenza e x la modalità.

Nota. La devianza è il numeratore della varianza.

Un esempio pratico

Esempio 1

Considero una distribuzione di valori composta da n=6 elementi

$$ 1 \ , \ 5 \ , \ 7 \ , \ 3 \ , \ 6 \ , \ 8 $$

La media aritmetica è μ=5

$$ \mu = \frac{1+5+7+3+6+8}{6 } = \frac{30}{6 } = 5 $$

Calcolo la devianza della distribuzione

$$ D(x) = \sum_{i=1}^n (x_i - \mu)^2 $$

$$ D(x) = (1-5)^2 + (5-5)^2 + (7-5)^2 + (3-5)^2 + (6-5)^2 + (8-5)^2 $$

$$ D(x) = (-4)^2 + (0)^2 + (2)^2 + (-2)^2 + (1)^2 + (3)^2 $$

$$ D(x) = 16 + 0 + 4 + 4 + 1 +9 $$

$$ D(x) = 34 $$

Pertanto, la devianza della serie di valori è 34.

Esempio 2

Considero questa distribuzione di frequenze

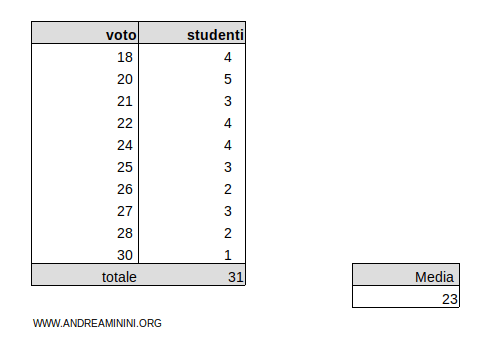
La media aritmetica ponderata dei dati è μ=23

Per calcolare la devianza utilizzo la formula delle distribuzioni di frequenze

$$ D(x) = \sum_{i=1}^n (x_i - \mu)^2 \cdot n_i $$

$$ D(x) = (18 - 23 )^2 \cdot 4 + (20 - 23 )^2 \cdot 5 + (21 - 23 )^2 \cdot 3 + (22 - 23 )^2 \cdot 4 + (24 - 23 )^2 \cdot 4 + \\ + (25 - 23 )^2 \cdot 3 + (26 - 23 )^2 \cdot 2 + (27 - 23 )^2 \cdot 3 + (28 - 23 )^2 \cdot 2 + (30- 23 )^2 \cdot 1 $$

$$ D(x) = (-5)^2 \cdot 4 + (-3)^2 \cdot 5 + (-2)^2 \cdot 3 + (-1)^2 \cdot 4 + (1)^2 \cdot 4 + \\ + (2)^2 \cdot 3 + (3)^2 \cdot 2 + (4)^2 \cdot 3 + (5)^2 \cdot 2 + (7)^2 \cdot 1$$

$$ D(x) = 25 \cdot 4 +9 \cdot 5 + 4 \cdot 3 +1 \cdot 4 + 1 \cdot 4 +4 \cdot 3 + 9 \cdot 2 + 16 \cdot 3 + 25 \cdot 2 + 49 \cdot 1 $$

$$ D(x) = 100 +45 + 12 +4 + 4 +12 + 18 + 48 + 50+ 49 $$

$$ D(x) = 342 $$

Pertanto, la devianza statistica della distribuzione di frequenze è 342.

Osservazioni

Alcune osservazioni sulla devianza

• Una formula alternativa per calcolare la devianza in una serie di dati è $$ D(x) = \sum_{i=1}^n x_i^2 - \mu \sum_{i=1}^n x_i $$

  Esempio. Considero una distribuzione di valori composta da n=6 elementi con la media aritmetica μ=5 $$ 1 \ , \ 5 \ , \ 7 \ , \ 3 \ , \ 6 \ , \ 8 $$ Calcolo la devianza usando la formula semplificata $$ D(x) = \sum_{i=1}^n x_i^2 - \mu \sum_{i=1}^n x_i $$ $$ D(x)= (1^2+5^2+7^2+3^2+6^2+8^2) - 5 \cdot (1+5+7+3+6+8) $$ $$ D(x)= (1+25+49+9+36+64) - 5 \cdot 30 $$ $$ D(x)= 184 - 150 $$ $$ D(x) = 34 $$

• Una formula alternativa per calcolare la devianza in una distribuzione di frequenze è $$ D(x) = \sum_{i=1}^n x^2_i n_i - \mu^2 \sum_{i=1}^n n_i $$

  Dimostrazione. Considero la formula della devianza di una distribuzione di frequenza $$ D(x) = \sum_{i=1}^k (x_i - \mu)^2 \cdot n_i $$ Sviluppo il quadrato del binomio $$ D(x) = \sum_{i=1}^k (x_i^2 + \mu^2 - 2x_i\mu) \cdot n_i $$ $$ D(x) = \sum_{i=1}^k x_i^2n_i + \mu^2n_i - 2x_i\mu n_i $$ Applico le proprietà delle serie $$ D(x) = \sum_{i=1}^k x_i^2n_i + \sum_{i=1}^k \mu^2n_i - 2 \sum_{i=1}^k x_i\mu n_i $$ $$ D(x) = \sum_{i=1}^k x_i^2n_i + \mu^2 \sum_{i=1}^k n_i - 2 \sum_{i=1}^k x_i\mu n_i $$ $$ D(x) = \sum_{i=1}^k x_i^2n_i + \mu^2 \sum_{i=1}^k n_i - 2 \mu \sum_{i=1}^k x_i n_i $$ Sapendo che la media aritmetica è μ=Σx_in_i/Σn_i allora Σx_in_i= μΣn_i $$ D(x) = \sum_{i=1}^k x_i^2n_i + \mu^2 \sum_{i=1}^k n_i - 2 \mu \cdot ( \mu \sum_{i=1}^k n_i )$$ $$ D(x) = \sum_{i=1}^k x_i^2n_i + \mu^2 \sum_{i=1}^k n_i - 2 \mu^2 \sum_{i=1}^k n_i $$ Sommo il secondo e il terzo termine tra loro $$ D(x) = \sum_{i=1}^k x_i^2n_i - \mu^2 \sum_{i=1}^k n_i $$

E così via.