La deviazione standard campionaria
La deviazione standard campionaria stima la dispersione di una popolazione intorno alla media a partire dalla deviazione standard misurata su un campione casuale estratto dalla popolazione. $$ \sigma = \sqrt{ \frac{1}{n-1} \cdot \sum_{i=1}^n (x_i-\mu)^2 } $$ Dove n è il numero di elementi nel campione e μ è la media dei valori nel campione.
E' la radice quadrata della varianza campionaria.
A cosa serve?
Utilizzo la formula della deviazione standard campionaria quando non posso calcolare la deviazione standard sull'intera popolazione per motivi tecnici o economici.
Ad esempio, se l'indagine statistica comporta la distruzione del campione o quando la popolazione è molto grande.
Qual è la differenza rispetto alla deviazione standard? La deviazione standard, o scarto quadratico medio, si calcola considerando gli n elementi della popolazione al denominatore. $$ \sigma = \sqrt{ \frac{1}{n} \cdot \sum_{i=1}^n (x_i-\mu)^2 } $$ La deviazione standard campionaria, invece, va corretta inserendo n-1 al denominatore, in questo caso n è il numero di elementi del campione, perchè è un'indagine effettuata su una minore quantità di unità e per tale ragione tende a sottostimare la deviazione standard sull'intera popolazione. $$ \sigma = \sqrt{ \frac{1}{n-1} \cdot \sum_{i=1}^n (x_i-\mu)^2 } $$
Un esempio pratico
Una scuola è frequentata da una popolazione di 1000 studenti.
Per evitare un'indagine sull'intera popolazione, stimo l'altezza media e la deviazione standard su un campione di 10 studenti.
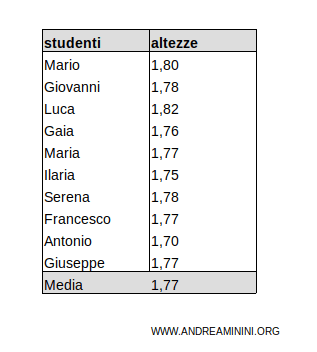
La media delle altezze nel campione è 1,77 cm.
$$ \mu = 1,77 $$
Sapendo che il campione è composto da n=10 unità, calcolo la deviazione standard campionaria
$$ \sigma = \sqrt{ \frac{1}{n-1} \cdot \sum_{i=1}^n (x_i-\mu)^2 } $$
$$ \sigma = \sqrt{ \frac{1}{10-1} \cdot \sum_{i=1}^n (x_i - 1,77)^2 } $$
$$ \sigma = \sqrt{ \frac{1}{9} \cdot [ ( 1,80-1,77)^2+( 1,78-1,77)^2+( 1,82-1,77)^2+ ( 1,76-1,77)^2+ \\ \ \ \ \ +( 1,77-1,77)^2+( 1,75-1,77)^2+( 1,78-1,77)^2+ \\ \ \ \ \ + ( 1,77-1,77)^2+( 1,70-1,77)^2+( 1,77-1,77)^2 ] } $$
$$ \sigma = \sqrt{ \frac{1}{9} \cdot [ ( 0,03)^2+( 0,01)^2+( 0,05)^2+( 0,01)^2+( 0)^2+ \\ \ \ \ \ +( -0,02)^2+( 0,01)^2+( 0)^2+( -0,07)^2+(0)^2 ] } $$
$$ \sigma = \sqrt{ \frac{1}{9} \cdot [ 0,0009+ 0,0001+0,0025+0,0001+0,0004+0,0001+0,0049 ] } $$
$$ \sigma = \sqrt{ \frac{1}{9} \cdot 0,009 } $$
$$ \sigma = \sqrt{ 0,001 } $$
Quindi, la deviazione standard campionaria è σ=0,0316
$$ \sigma = 0,0316 $$
In questo modo ottengo indirettamente una stima della deviazione standard della popolazione di 1000 studenti intorno all'altezza media.
Nota. Se avessi usato la formula della deviazione standard (non campionaria) il risultato sarebbe stato più basso. $$ \sigma = \sqrt{ \frac{1}{n} \cdot \sum_{i=1}^n (x_i-\mu)^2 } = \sqrt{ \frac{1}{10} \cdot 0,009 } = 0,03 $$ Per questa ragione la deviazione standard campionaria viene corretta usando un denominatore inferiore (n-1). $$ \sigma = \sqrt{ \frac{1}{n-1} \cdot \sum_{i=1}^n (x_i-\mu)^2 } = \sqrt{ \frac{1}{9} \cdot 0,009 } = 0,0316 $$
E così via.
