La concentrazione della variabilità
La concentrazione misura la variabilità di un fenomeno additivo. In altre parole, misura quanto sono concentrati i dati in una variabile statistica X.
La concentrazione è compresa tra due situazioni estreme
- Massima concentrazione
Se una sola unità ha l'intero ammontare della variabile statistica X, la concentrazione è massima. - Equidistribuzione
Se tutte le unità hanno lo stesso ammontare del carattere,allora la concentrazione è nulla. Si verifica l'equidistribuzione. E' anche conosciuta come "concentrazione nulla".
Come si misura la concentrazione
Se una variabile statistica ha n modalità di natura quantitativa, ordino le n modalità in ordine non decrescente. Dalla più piccola alla più grande.
$$ x_{1},x_{2},...,x_{n} $$
Esempio. Ho la distribuzione X composta da 8 valori
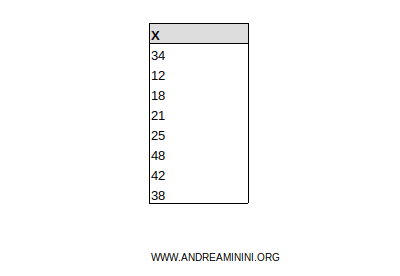
Ordino i dati in modo non decrescente.
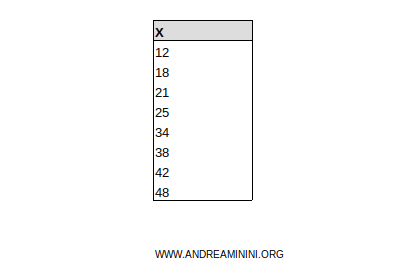
Poi suddivido le n unità osservate in n frazioni cumulate (pi) che chiamo frazioni cumulate delle unità.
$$ p_1 = \frac{1}{n} \\ p_2 = \frac{2}{n} \\ \vdots \\ p_n = \frac{n}{n} = 1 $$
Esempio. Nella distribuzione X ci sono n=8 unità osservate. Quindi, le frazioni cumulate delle unità sono $$ p_1 = \frac{1}{8} = 0,125 \\ p_2 = \frac{2}{8} = 0,25 \\ p_3 = \frac{3}{8} = 0,375 \\ p_4 = \frac{4}{8} = 0,5 \\ p_2 = \frac{5}{8} = 0,625 \\ p_6 = \frac{6}{8} = 0,75 \\ p_7 = \frac{7}{8} = 0,875 \\ p_8 = \frac{8}{8} = 1 $$ Le aggiungo nella tabella precedente.
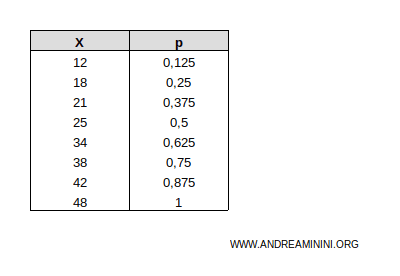
Le frazioni cumulate delle unità sono valori da 0 a 1.
Calcolo il totale xtot del carattere nella variabile statistica
$$ x_{tot} = \sum_{i=1}^n x_{i} $$
Esempio. In questo caso il totale delle osservazioni è xtot=238
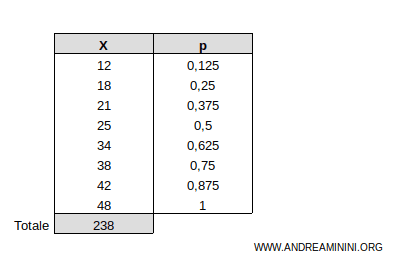
Aggiungo il cumulato x' delle osservazioni
Esempio. Aggiungo la colonna del cumulato x' alla tabella
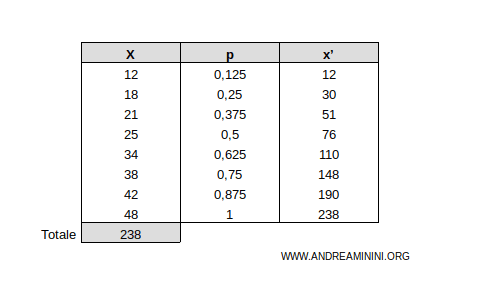
Infine, calcolo le frazioni cumulate del carattere.
$$ q_1 = \frac{1}{ x_{tot} } \cdot \sum_{i=1}^1 x_i $$
$$ q_2 = \frac{1}{ x_{tot} } \cdot \sum_{i=1}^2 x_i $$
$$ q_n = \frac{1}{ x_{tot} } \cdot \sum_{i=1}^n x_i = 1 $$
Anche in questo le frazioni cumulate del carattere sono valori compresi tra 0 e 1.
Esempio. Aggiungo la colonna q delle frazioni cumulate del carattere alla tabella.
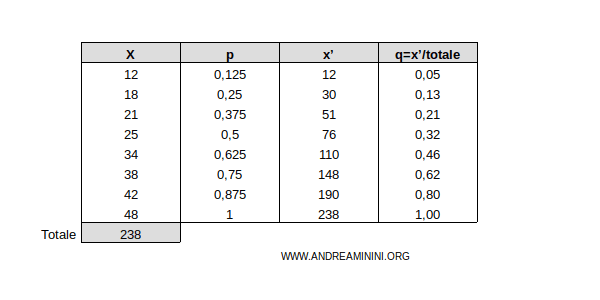
Il confronto tra le frazioni cumulate delle unità osservate (pi) e del carattere (qi) delinea un quadro della concentrazione dei dati.
Per fare questo confronto utilizzo la curva di Lorenz o curva della concentrazione.
Sull'area delle ascisse misuro le frazioni cumulate delle unità osservate (pi) mentre sull'asse delle ordinate misuro le frazioni cumulate del carattere (qi)
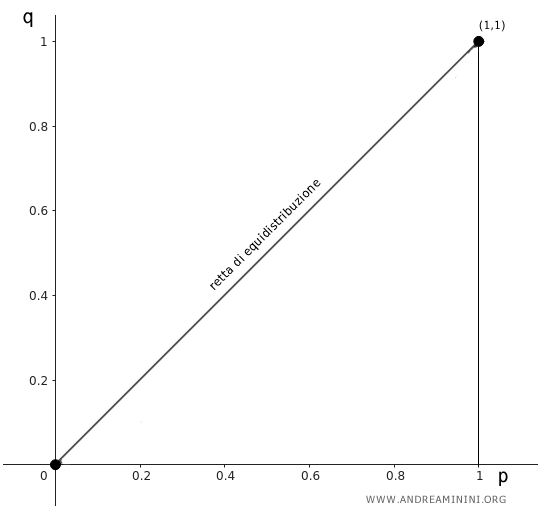
La diagonale dal punto di origine (0;0) al punto (1;1) in alto a destra identifica la retta di equidistribuzione.
Se ci fosse un'equidistribuzione del carattere tutti i punti si collocherebbero su questa retta.
Infine, traccio dei punti nelle coordinate (pi,qi) per i=1,...,n.
Quando unisco questi punti ottengo la curva di concentrazione della variabile statistica.
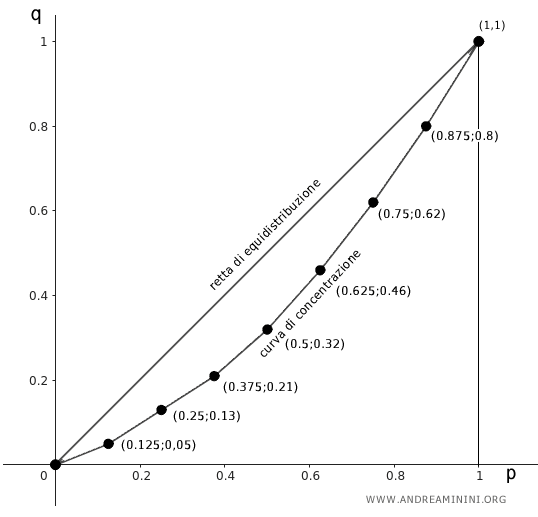
L'area compresa tra la retta di equidistribuzione e la curva di concentrazione misura la concentrazione della variabile statistica ed è detta area di concentrazione (A).
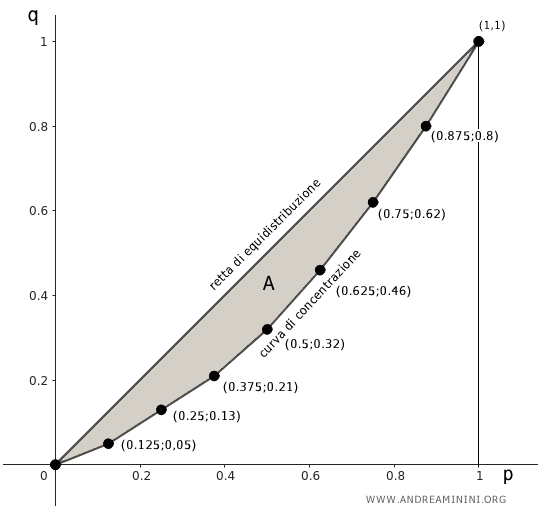
L'indice della concentrazione (R) è dato dal rapporto tra l'area di concentrazione (A) e l'area di massima concentrazione.
$$ R = \frac{ \text{area di concentrazione (A)} }{ \text{area di max. concentrazione} } $$
Questo indice misura la concentrazione dei dati tra 0 e 1, dove 1 rappresenta la massima concentrazione.
Un esempio pratico
Faccio un esempio pratico per calcolare l'indice di concentrazione, utilizzando una distribuzione di valori e le loro frequenze.
Supponiamo di avere una distribuzione di redditi all'interno di un piccolo gruppo di persone.
| xi (reddito) | fi (frequenza) |
|---|---|
| 10.000 | 2 |
| 20.000 | 3 |
| 30.000 | 5 |
| 40.000 | 4 |
| 50.000 | 6 |
Questi valori rappresentano i redditi (\( x_i \)) di un gruppo di persone e le rispettive frequenze (\( f_i \)) indicano quante persone percepiscono ciascun reddito.
Moltiplico ogni \( x_i \) per la rispettiva frequenza \( f_i \):
| xi | fi | xi × fi |
|---|---|---|
| 10.000 | 2 | 20.000 |
| 20.000 | 3 | 60.000 |
| 30.000 | 5 | 150.000 |
| 40.000 | 4 | 160.000 |
| 50.000 | 6 | 300.000 |
Calcolo le frequenze relative (\( f_i / \sum f_i \)) e poi le sommo per ottenere le cumulate.
La somma delle frequenze (\( \sum f_i \)) è \( 2 + 3 + 5 + 4 + 6 = 20 \).
| xi | fi | Frequenza relativa (fi/20) | frc | xi × fi | Intensità relativa (∑ xi × fi / 690000) | irc |
|---|---|---|---|---|---|---|
| 10.000 | 2 | 0.10 | 0.10 | 20.000 | 0.029 | 0.029 |
| 20.000 | 3 | 0.15 | 0.25 | 60.000 | 0.087 | 0.116 |
| 30.000 | 5 | 0.25 | 0.50 | 150.000 | 0.217 | 0.333 |
| 40.000 | 4 | 0.20 | 0.70 | 160.000 | 0.232 | 0.565 |
| 50.000 | 6 | 0.30 | 1.00 | 300.000 | 0.435 | 1.000 |
Il totale delle intensità è pari a 690.000
$$ 20.000 + 60.000 + 150.000 + 160.000 + 300.000 = 690.000 $$
Le frequenze cumulate (\( f_{rc} \)) sono la somma progressiva delle frequenze relative.
Le intensità relative cumulate (\( i_{rc} \)) sono la somma progressiva delle intensità relative.
A questo punto, rappresento i punti \((f_{rc}; i_{rc})\) nel piano cartesiano e li colleghiamo per ottenere la spezzata di concentrazione.
| frc | irc |
|---|---|
| 0.10 | 0.029 |
| 0.25 | 0.116 |
| 0.50 | 0.333 |
| 0.70 | 0.565 |
| 1.00 | 1.000 |
Ecco il diagramma cartesiano che mostra la spezzata di concentrazione e la retta di equidistribuzione.
I punti rappresentano le frequenze relative cumulate (\( f_{rc} \)) e le intensità relative cumulate (\( i_{rc} \)), mentre la linea tratteggiata rappresenta la retta di equidistribuzione.
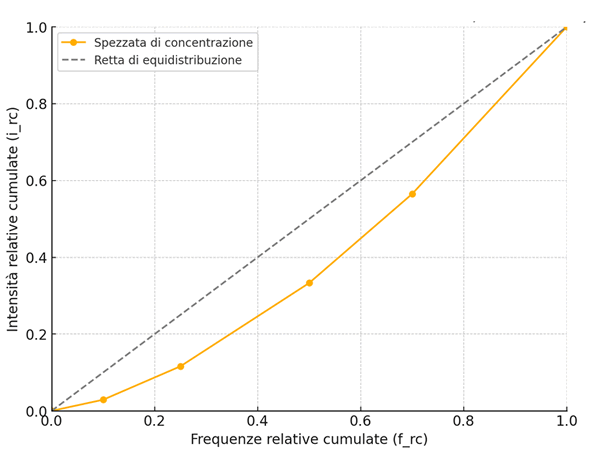
Per calcolare l'indice di concentrazione, devo calcolare l'area compresa tra la retta di equidistribuzione (la bisettrice del primo quadrante, ovvero \( y = x \)) e la spezzata di concentrazione.
L'area di massima concentrazione è sempre pari a 0,5.
Nota. L'area di massima concentrazione è pari a 0,5 perché rappresenta l'area del triangolo formato dalla retta di equidistribuzione \( y = x \) che descrive una distribuzione perfettamente equa, nel piano delle frequenze relative cumulate e delle intensità relative cumulate. Questa retta forma un triangolo con i punti (0,0), (1,0) e (1,1), con base e altezza pari a 1. L'area del triangolo è calcolata come: $$ \text{Area} = \frac{1 \times 1}{2} = 0,5 $$ Quest'area rappresenta il massimo possibile e viene usata per normalizzare l'area di concentrazione effettiva, permettendo così di calcolare l'indice di concentrazione \( R \).
Per misurare l'area di concentrazione devo calcolare l'area tra la spezzata e l'asse orizzontale delle frequenze cumulate.
Suddivido la zona sottesa in triangoli e trapezi in base ai punti della spezzata di concentrazione:
- \( (0.0, 0.0) \)
- \( (0.10, 0.029) \)
- \( (0.25, 0.116) \)
- \( (0.50, 0.333) \)
- \( (0.70, 0.565) \)
- \( (1.00, 1.000) \)
In questo modo ottengo cinque figure geometriche elementari, un triangolo e quattro trapezi.
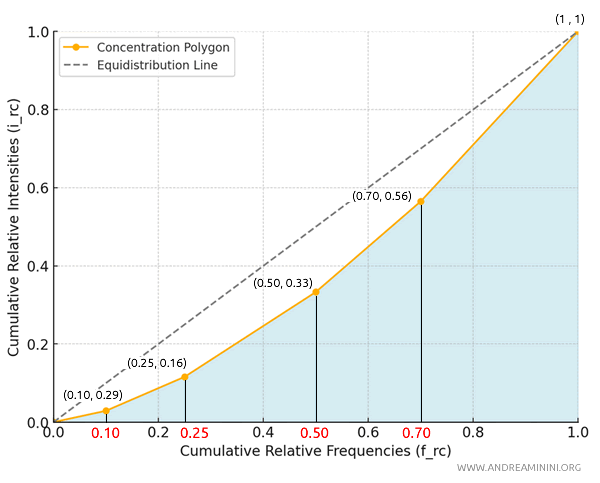
Il primo segmento parte dal punto \((0, 0)\) e arriva a \((0.10, 0.029)\).
Si tratta di un triangolo con base \( 0.10 - 0.00 = 0.10 \) e altezza \( 0.029 \)
Quindi, l'area del triangolo iniziale è:
$$ \text{Area} = 0.5 \times \text{Base} \times \text{Altezza} = 0.5 \times 0.10 \times 0.029 = 0.00145 $$
Per ciascun segmento successivo, calcolo l'area del trapezio usando la formula:
$$ \text{Area} = 0.5 \times (\text{Altezza}_1 + \text{Altezza}_2) \times (\text{Base}) $$
Il trapezio tra \((0.10, 0.029)\) e \((0.25, 0.116)\) ha come base: \( 0.25 - 0.10 = 0.15 \) e come altezze \( 0.029 \) e \( 0.116 \)
$$ \text{Area} = 0.5 \times (0.029 + 0.116) \times 0.15 = 0.010875 $$
Il trapezio tra tra \((0.25, 0.116)\) e \((0.50, 0.333)\) ha come base \( 0.50 - 0.25 = 0.25 \) e come altezze \( 0.116 \) e \( 0.333 \)
$$ \text{Area} = 0.5 \times (0.116 + 0.333) \times 0.25 = 0.056875 $$
Il trapezio tra \((0.50, 0.333)\) e \((0.70, 0.565)\) ha come base \( 0.70 - 0.50 = 0.20 \) e come altezze \( 0.333 \) e \( 0.565 \)
$$ \text{Area} = 0.5 \times (0.333 + 0.565) \times 0.20 = 0.089800 $$
Il trapezio tra \((0.70, 0.565)\) e \((1.00, 1.000)\) ha come base \( 1.00 - 0.70 = 0.30 \) e come altezze \( 0.565 \) e \( 1.000 \)
$$ \text{Area} = 0.5 \times (0.565 + 1.000) \times 0.30 = 0.234 $$
A questo punto, sommo le aree di tutti i trapezi e del triangolo:
$$ \text{Area totale} = 0.00145 + 0.010875 + 0.056875 + 0.089800 + 0.234 = 0.393 $$
L'area totale sottostante la spezzata di concentrazione, calcolata sommando le aree dei singoli trapezi e del triangolo, è risultata pari a 0.393.
Questo valore mi permette di calcolare l'area di concentrazione sottraendo l'area totale della spezzata (0.393) dall'area massima (0.5):
$$ \text{area di concentrazione} = 0.5 - 0.393 = 0.107 $$
L'area di concentrazione è pari a 0.107.
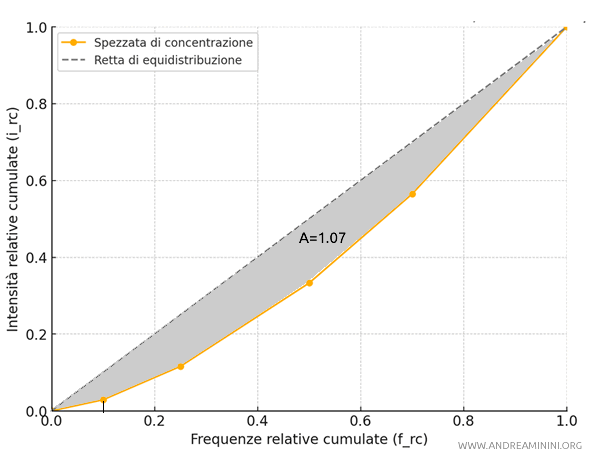
Pertanto, l'indice di concentrazione si calcola come segue:
$$ R = \frac{\text{area di concentrazione}}{\text{area di massima concentrazione}} = \frac{0,107}{0,5} = 0,214 $$
L'indice di concentrazione \( R = 0,214 \) indica che la distribuzione dei redditi nel gruppo è moderatamente concentrata, pari al 21,4%.
Un valore più vicino a 1 indica una maggiore concentrazione (una distribuzione non equa), mentre un valore vicino a 0 indica una distribuzione molto equa.
E così via.
