La differenza media

La differenza semplice media è un indice di variabilità basato sulle differenze in valore assoluto tra tutti gli elementi di una distribuzione presi a coppia. $$ \Delta = \frac{1}{n \cdot (n-1)} \cdot \sum_{i=1}^n \sum_{j=1}^n |x_i-x_j| $$ Dove n è il numero di elementi di una distribuzione.

Le distanze interne sono calcolate in valore assoluto perché, altrimenti, i valori opposti (es. 2 e -2) si annullerebbero reciprocamente.

Il denominatore della differenza semplice media è uguale al numero delle combinazioni n(n-1) tra gli elementi, escludendo i confronti tra gli stessi elementi della distribuzione che si annullano reciprocamente.

Nota. Nel caso in cui volessi considerare anche il confronto tra gli stessi elementi della distribuzione dovrei usare la formula della differenza media con ripetizione. $$ \Delta = \frac{1}{n \cdot (n-1)} \cdot \sum_{i=1}^n \sum_{j=1}^n |x_i-x_j| $$ In questo caso le combinazioni tra gli elementi sono n·n ossia n².

Un esempio pratico

Ho una distribuzione composta da n=3 elementi

$$ X = \{ 2, 5, 6 \} $$

La differenza semplice media è la seguente

$$ \Delta = \frac{1}{n \cdot (n-1)} \cdot \sum_{i=1}^n \sum_{j=1}^n |x_i-x_j| $$

$$ \Delta = \frac{1}{3 \cdot 2} \cdot \sum_{i=1}^3 \sum_{j=1}^3 |x_i-x_j| $$

$$ \Delta = \frac{1}{6} \cdot ( |2-2| + |2-5|+ |2-6| + |5-2| + |5-5|+ |5-6| + |6-2| + |6-5|+ |6-6| )$$

$$ \Delta = \frac{1}{6} \cdot ( |0| + |-3|+ |-4| + |3| + |0|+ |-1| + |4| + |1|+ |0| )$$

$$ \Delta = \frac{1}{6} \cdot ( 3+4+3+1+4+1)$$

$$ \Delta = \frac{1}{6} \cdot 16 $$

Quindi, la differenza semplice media è

$$ \Delta = 2,66 $$

Nota. Se avessi voluto calcolare la differenza semplice media con ripetizione avrei dovuto utilizzare n² al denominatore. $$ \Delta_R = \frac{1}{3^2} \cdot \sum_{i=1}^3 \sum_{j=1}^3 |x_i-x_j| $$ $$ \Delta_R = \frac{1}{9} \cdot 16 $$ $$ \Delta_R = 1,77 $$

Il metodo delle distanze graduali

Un modo alternativo per calcolare la differenza media semplice si basa sulle distanze graduali.

Ordino la distribuzione X in modo non decrescente.

$$ X = \{ 2, 5, 6 \} $$

Poi costruisco la matrice delle differenze

Nel caso della distribuxione X={2,5,6} la matrice delle differenze è la seguente

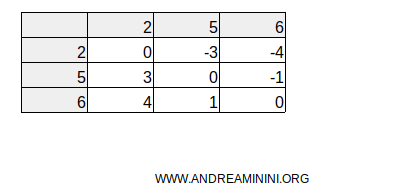
Come si può facilmente vedere, la matrice triangolare inferiore è composta solo da differenze positive.

La matrice triangolare superiore è invece composta dalle differenze negative.

Le differenze negative non mi servono, quindi le elimino.

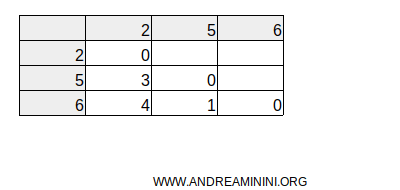
Aggiungo la somma delle differenze positive sotto ogni colonna (modalità)

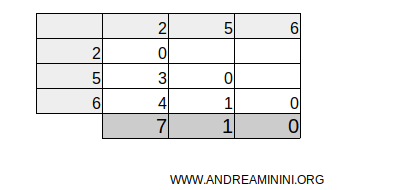
Poi calcolo la somma delle somme.

In questo caso la somma totale è uguale a S=8

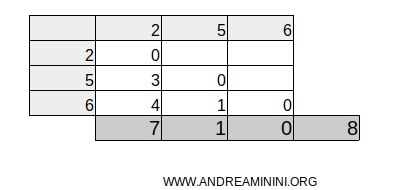
A questo punto calcolo la differenza media usando questa formula

$$ \Delta = \frac{2 \cdot S}{n \cdot (n-1)} $$

Sapendo che S=8 e n=3

$$ \Delta = \frac{2 \cdot 8}{3 \cdot (3-1)} $$

$$ \Delta = \frac{16}{3 \cdot 2} $$

$$ \Delta = \frac{16}{6} $$

Quindi, la differenza media è 2,66

$$ \Delta = 2,66 $$

Il risultato finale è lo stesso dell'esempio precedente.

Osservazioni

Alcune osservazioni sulla differenza media

• La differenza semplice media con e senza ripetizione sono legate tra loro dalla relazione $$ \Delta = \Delta_R \cdot \frac{n}{n-1} $$

  Nota. Nell'esempio precedente ho calcolato $$ \Delta = 2,66 $$ $$ \Delta_R = 1,77 $$ La relazione tra i due indici è $$ \Delta = \Delta_R \cdot \frac{n}{n-1} $$ $$ 2,66 =1,77 \cdot \frac{3}{3-1} $$ $$ 2,66 = \frac{1,77 \cdot 3}{2} $$ $$ 2,66 = 2,66 $$

• La differenza media è un valore compreso non negativo (Δ≥0). Assume il valore minimo (Δ=0) quando tutti gli elementi della distribuzione sono uguali.
• Posso calcolare la differenza media anche in questo modo alternativo:
  
  
  1. ordino gli elementi della distribuzione in modo non decrescente
  2. applico questa formula $$ \Delta = \frac{1}{n(n-1)} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{2 \mu (n+1) }{n-1} $$

  Esempio. Considero la stessa distribuzione banale dell'esempio precedente composta da n=3 elementi $$ X = \{ 2, 5, 6 \} $$ La media della distribuzione è $$ \mu= \frac{2+5+6}{3} = \frac{13}{3} = 4,33333 $$ Applico la formula per calcolare la differenza media $$ \Delta = \frac{1}{n(n-1)} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{2 \mu (n+1) }{n-1} $$ $$ \Delta = \frac{1}{3(3-1)} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{2 \cdot 4,33333 \cdot (3+1) }{3-1} $$ $$ \Delta = \frac{1}{3 \cdot 2} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{8,66666 \cdot 4 }{2} $$ $$ \Delta = \frac{1}{6} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{34,6666 }{2} $$ $$ \Delta = \frac{2}{3} \cdot \sum_i^n (i \cdot x_i) - 17,3333 $$ $$ \Delta = \frac{2}{3} \cdot [ (1 \cdot 2) + (2 \cdot 5) + (3 \cdot 6) ] - 17,3333 $$ $$ \Delta = \frac{2}{3} \cdot [ 2 + 10 + 18 ] - 17,3333 $$ $$ \Delta = \frac{2}{3} \cdot 30 - 17,3333 $$ $$ \Delta = 20 - 17,3333 $$ $$ \Delta = 2,66 $$ Il risultato finale è lo stesso dell'esempio precedente.

• Posso calcolare la differenza media con ripetizione anche in questo modo alternativo:
  
  
  1. ordino gli elementi della distribuzione in modo non decrescente
  2. applico questa formula $$ \Delta = \frac{1}{n^2} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{2 \mu (n+1) }{n} $$

  Esempio. Considero la stessa distribuzione banale dell'esempio precedente composta da n=3 elementi $$ X = \{ 2, 5, 6 \} $$ La media della distribuzione è $$ \mu= \frac{2+5+6}{3} = \frac{13}{3} = 4,33333 $$ Applico la formula per calcolare la differenza media con ripetizione $$ \Delta = \frac{1}{n^2} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{2 \mu (n+1) }{n} $$ $$ \Delta = \frac{1}{3^2} \cdot 4 \sum_i^n (i \cdot x_i) - \frac{2 \cdot 4,33333 \cdot (3+1) }{3} $$ $$ \Delta = \frac{4}{9} \cdot \sum_i^n (i \cdot x_i) - \frac{8,66666 \cdot (4) }{3} $$ $$ \Delta = \frac{4}{9} \cdot \sum_i^n (i \cdot x_i) - \frac{34,6666}{3} $$ $$ \Delta = \frac{4}{9} \cdot \sum_i^n (i \cdot x_i) - 11,5555 $$ $$ \Delta = \frac{4}{9} \cdot [ (1 \cdot 2) + (2 \cdot 5) + (3 \cdot 6) ] - 11,5555 $$ $$ \Delta = \frac{4}{9} \cdot [ 2 +10 + 18 ] - 11,5555 $$ $$ \Delta = \frac{4}{9} \cdot 30 - 11,5555 $$ $$ \Delta = 13,3333 - 11,5555 $$ $$ \Delta = 1,77 $$ Il risultato è lo stesso dell'esempio precedente.

• Nel caso delle distribuzioni di frequenza posso calcolare la differenza media con ripetizione usando questa formula $$ \Delta_R = \frac{2}{n^2} \sum_{i=1}^{k-1} c_i(n-c_i)(x_{i+1} - x_i) $$ Dove n è il totale delle frequenze, n_i è la frequenza della i-esima classe, c_i è il cumulato delle frequenze (n) fino alla i-esima classe, x_i sono le modalità.

  Esempio. Considero questa distribuzione di frequenza composta da k=7 modalità.
  
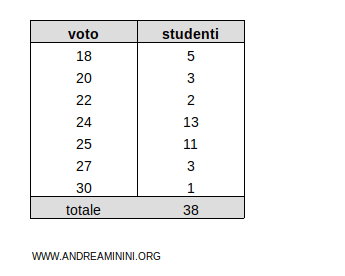
  La differenza media è la seguente: $$ \Delta_R = \frac{2}{n^2} \sum_{i=1}^{k-1} c_i(n-c_i)(x_{i+1} - x_i) $$ $$ \Delta_R = \frac{2}{38^2} \sum_{i=1}^{7-1} c_i(38-c_i)(x_{i+1} - x_i) $$ $$ \Delta_R = \frac{2}{1444} \sum_{i=1}^{6} c_i(38-c_i)(x_{i+1} - x_i) $$ In questo caso la sommatori aè uguale a 2098
  
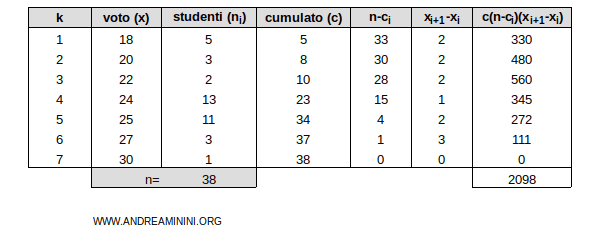
  Quindi, la differenza media della distribuzione di frequenze è 2,9 $$ \Delta_R = \frac{2}{1444} \cdot 2098 $$ $$ \Delta_R = 2,9 $$

E così via.