Lo scostamento semplice medio

Cos'è lo scostamento medio

Lo scostamento medio è un indice di variabilità che somma il valore assoluto degli scarti, ossia della differenza di ogni elemento della distribuzione (x_i) rispetto al valore medio (μ). $$ S = \frac{1}{n} \cdot \sum_{i=1}^n | x_i - \mu | $$ Dove μ può essere la media aritmetica o la mediana

E' anche detto scarto semplice medio ed è uno degli indicatori di variabilità assoluta.

A cosa serve?

Lo scostamento semplice medio mi fornisce una misura della dispersione dei dati all'interno di una popolazione o di una distribuzione statistica.

Gli scarti rispetto alla media vanno presi in valore assoluto perché altrimenti si compenserebbero tra loro, senza fornire nessuna informazione sulla dispersione.

Nota. Nel caso di una distribuzione di frequenze, per calcolare lo scostamento medio uso questa formula. $$ S = \frac{ \sum |x_i - \mu| \cdot n_i}{ \sum n_i } $$

Un esempio pratico

Considero questa distribuzione statistica con n=6 elementi

$$ x = \{ 4, 2, 6, 8, 7, 3 \} $$

La media aritmetica della distribuzione è m=5

$$ mu = \frac{4+2+6+8+7+3}{6} = \frac{30}{6} = 5 $$

A questo punto calcolo lo scostamento medio rispetto alla media aritmetica

$$ S = \frac{1}{n} \cdot [ |4- \mu| + |2 - \mu | + |6 - \mu| + |8 - \mu| + |7- \mu | + | 3 - \mu | ] $$

Sapendo che il numero di elementi è n=6 e la media aritmetica è m=5

$$ S = \frac{1}{6} \cdot [ |4- 5| + |2 - 5 | + |6 - 5| + |8 - 5| + |7- 5 | + | 3 - 5 | ] $$

$$ S = \frac{1}{6} \cdot [ |-1| + | -3 | + |1| + |3| + |2 | + | -2 | ] $$

$$ S = \frac{1}{6} \cdot [ 1 + 3 + 1 + 3 + 2 + 2 ] $$

$$ S = \frac{1}{6} \cdot 12 $$

$$ S = 2 $$

Lo scostamento medio è uguale a S=2

Esempio 2

Considero questa distribuzione di frequenze in cui i voti sono le modalità

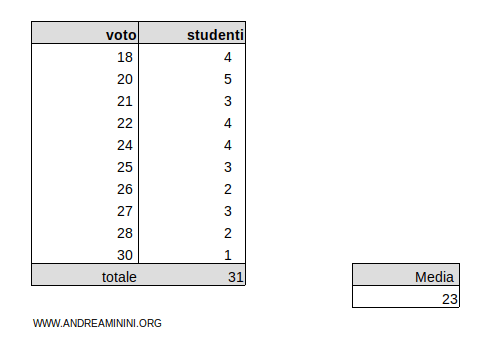
La media aritmetica ponderata è uguale μ=23

Per calcolare lo scostamento semplice medio uso la formula

$$ S = \frac{ \sum |x_i - \mu| \cdot n_i}{ \sum n_i } $$

Dove x_i sono i voti e n_i sono le frequenze dei voti.

La somma delle frequenze Σn=31 e la media è μ=23

$$ S = \frac{ \sum |x_i - 23| \cdot n_i}{ 31 } $$

$$ S = \frac{ |18-23| \cdot 4 + |20-23| \cdot 5 + |21-23| \cdot 3 + |22-23| \cdot 4 + |24-23| \cdot 4 + \\ + |25-23| \cdot 3 + |26-23| \cdot 2 + |27-23| \cdot 3 + |28-23| \cdot 2 + |30-23| \cdot 1 }{ 31 } $$

$$ S = \frac{ |-5| \cdot 4 + |-3| \cdot 5 + |-2| \cdot 3 + |-1| \cdot 4 + |1| \cdot 4 + \\ + |2| \cdot 3 + |3| \cdot 2 + |4| \cdot 3 + |5| \cdot 2 + |7| \cdot 1 }{ 31 } $$

$$ S = \frac{ 5 \cdot 4 + 3 \cdot 5 + 2 \cdot 3 + 1 \cdot 4 + 1 \cdot 4 + 2 \cdot 3 + 3 \cdot 2 + 4 \cdot 3 + 5 \cdot 2 + 7 \cdot 1 }{ 31 } $$

$$ S = \frac{ 20 + 15 + 6 + 4 + 4 + 6 + 6 + 12 + 10 + 7 }{ 31 } $$

$$ S = \frac{ 90 }{ 31 } $$

$$ S = 2,9 $$

Lo scarto semplice medio della distribuzione è S=2,9

Note

Alcune osservazioni e note a margine

• Perché gli scarti sono presi in valore assoluto?
  Nello scarto semplice medio si utilizzano i valori assoluti delle deviazioni dalla media per evitare che scarti positivi e negativi (rispetto alla media) si compensino annullandosi a vicenda. In particolare, la media aritmetica degli scarti dalla media senza considerare i valori assoluti è sempre zero e questo non fornisce alcuna informazione utile sulla variabilità o dispersione dei dati. Ad esempio, considero una distribuzione di n valori x₁,x₂,...,x_n che hanno la media aritmetica μ. La media degli scarti senza i valori assoluti è la seguente: $$ \frac{(x_1 - \mu)+(x_2 - \mu)+...+(x_n - \mu)+ }{n} $$ Applico la proprietà associativa e commutativa dell'addizione $$ \frac{x_1+x_2+...+x_n - \underbrace{ \mu - \mu- \mu}_{n \ volte} }{n} $$ La media aritmetica μ si ripete n volte $$ \frac{x_1+x_2+...+x_n - n \cdot \mu }{n} $$ Quindi, semplifico algebricamente $$ \frac{x_1+x_2+...+x_n }{n} - \frac{n \cdot \mu}{n} $$ $$ \underbrace{ \frac{x_1+x_2+...+x_n}{n} }_{ \mu } - \mu $$ Poiché il primo addendo è sempre la media aritmetica $ \mu =  \frac{x_1+x_2+...+x_n }{n} $, la somma si annulla. $$ \mu - \mu = 0 $$ Pertanto, la somma degli scarti rispetto alla media è sempre nulla. Per questa ragione lo scarto semplice medio si basa sui valori assoluti, per evitare l'annullamento reciproco degli scarti e per ottenere una misura efficace della dispersione dei dati.

  Esempio. Considero la distribuzione $$ 2, 4, 6, 8, 10 $$ La media aritmetica di questi numeri è 6. $$ \mu = \frac{2+4+6+8+10}{5} = \frac{30}{5} = 6 $$ Gli scarti dalla media sono: $$ 2 - 6 = -4 \\ 4 - 6 = -2 \\ 6 - 6 = 0 \\ 8 - 6 = 2 \\ 10 - 6 = 4 $$ La somma degli scarti è sempre nulla $$ (-4) + (-2) + 0 + 2 + 4 = 0 $$ In questo caso, la media aritmetica degli scarti non mi dice nulla sulla dispersione. $$ \frac{(-4) + (-2) + 0 + 2 + 4}{5} = \frac{0}{5}=0 $$ Invece, usando i valori assoluti la somma degli scarti è sempre un valore non negativo: $$ |-4| + |-2| + |0| + |2| + |4| = 4+2+0+2+4= 12 $$ Quindi, anche la media aritmetica degli scarti assoluti è un valore non negativo $$ \frac{4 + 2 + 0 + 2 + 4}{5} = 2.4 $$ Questo valore indica la dispersione media dei dati rispetto alla media aritmetica.

E così via.