Come capire se tre punti sono allineati

Nel piano tre punti A,B,C sono punti allineati se esiste una retta che li comprende.

Dati tre punti qualsiasi del piano

$$ P_A = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} $$ $$ P_B = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$ $$ P_C = \begin{pmatrix} x_3 \\ y_3 \end{pmatrix} $$

Ecco la rappresentazione grafica di tre punti allineati.

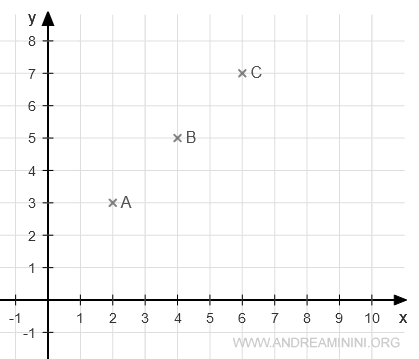
I punti A,B,C hanno le seguenti coordinate: $$ P_A = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$ $$ P_B = \begin{pmatrix} 4 \\ 5 \end{pmatrix} $$ $$ P_C = \begin{pmatrix} 6 \\ 7 \end{pmatrix} $$

Congiungendo il punto A con B ottengo il vettore AB.

$$ v_1 = \overrightarrow{AB} = P_B - P_A $$

$$ v_1 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} $$

$$ v_1 = \begin{pmatrix} x_2-x_1 \\ y_2-y_1 \end{pmatrix} $$

$$ v_1 = \begin{pmatrix} 4-2 \\ 5-3 \end{pmatrix} $$

$$ v_1 = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Congiungendo il punto A con C ottengo il vettore AC.

$$ v_2 = \overrightarrow{AC} = P_C - P_A $$

$$ v_2 = \begin{pmatrix} x_3 \\ y_3 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} x_3-x_1 \\ y_3-y_1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 6-2 \\ 7-3 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 4 \\ 4 \end{pmatrix} $$

Se tre punti A,B,C punti sono allineati, allora i vettori AB e AC sono vettori linearmente dipendenti.

Il motivo è molto semplice, i vettori v₁ e v₂ risiedono sulla stessa retta.

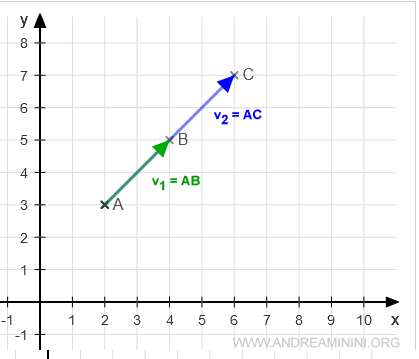
Quindi, posso definire ogni vettore v₁ e v₂ come combinazione lineare dell'altro.

$$ v_1 = a_1 \cdot v_2 $$

$$ v_2 = a_2 \cdot v_3 $$

Dove i coefficienti a₁ e a₂ sono due numeri scalari.

Esempio. Le combinazioni lineari dell'esempio precedente sono le seguenti: $$ v_1 = a_1 \cdot v_2 \\ \begin{pmatrix} 2 \\ 2 \end{pmatrix} = a_1 \cdot \begin{pmatrix} 2 \\ 2 \end{pmatrix} \:\:con\:\: a_1 = 1/2 $$ $$ v_2 = a_2 \cdot v_1 \\ \begin{pmatrix} 4 \\ 4 \end{pmatrix} = a_2 \cdot \begin{pmatrix} 2 \\ 2 \end{pmatrix} \:\:con\:\: a_2 = 2 $$

Ogni vettore è multiplo o sottomultiplo dell'altro.

Pertanto, i vettori AB e AC sono vettori proporzionali tra loro.

Quindi, secondo la regola dei vettori proporzionali, il determinante della matrice composta dai vettori AB e BC è nullo.

$$ det \begin{pmatrix} x_2-x_1 & x_3-x_1 \\\ y_2-y_1 & y_3-y_1 \\ \end{pmatrix} $$

Esempio. Il determinante dei vettori v₁ e v₂ è uguale a zero. $$ det \begin{pmatrix} 2 & 4 \\ 2 & 4 \\ \end{pmatrix} = ( 2 \cdot 4 ) - ( 4 \cdot 2 ) = 0 $$