Volume
Il volume in fisica è definito come la quantità di spazio occupata da un corpo o un oggetto.
È una grandezza fisica fondamentale che viene misurata in metri cubi (m³) nel Sistema Internazionale (SI), ma può essere anche espressa in altre unità, come i litri (L) per i liquidi.
In analisi dimensionale, il volume è espresso come una grandezza fisica derivata dalle lunghezze, quindi la sua dimensione si indica con:
$$ [V] = [L^3] $$
Dove \( L \) rappresenta la dimensione della lunghezza.
Questa notazione indica che il volume è il prodotto di tre lunghezze.
Ad esempio, quando calcolo il volume di un parallelepipedo rettangolare, moltiplico la lunghezza, la larghezza e l'altezza (tutte espresse in unità di lunghezza) e ottengo un volume in unità cubiche.
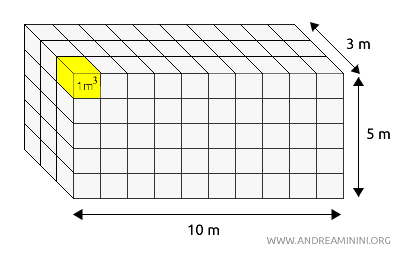
In questo caso il parallelepipedo ha una lunghezza di 10 metri, una larghezza di 3 metri e un'altezza di 5 metri. Quindi, il suo volume è il prodotto di tre lunghezze.
$$ V = 10 \ m \cdot 3 \ m \cdot 5 \ m = (10 \cdot 3 \cdot 5 ) m^3 = 150 \ m^3 $$
Dal punto di vista dimensionale si scrive \( [L^3] \).
Questa notazione è di fondamentale importanza in fisica, perché mi permette di verificare la correttezza dimensionale delle equazioni prima di controllare i calcoli, e di comprendere come le grandezze fisiche si relazionano tra loro.
Il volume è essenziale per determinare altre proprietà fisiche come la densità, che è il rapporto tra la massa e il volume di un oggetto (Densità = Massa / Volume). E' particolarmente utile in fisica e chimica per calcolare la quantità di sostanza in un dato spazio, specialmente per i gas e i liquidi.
La formula del volume
Il volume dipende dalla forma dell'oggetto. Ad esempio:
- Cubo $$ V = l^3 $$ dove \( l \) è la lunghezza di uno dei lati del cubo.
- Parallelepipedo rettangolare $$ V = l \cdot w \cdot h $$ dove \( l \), \( w \) e \( h \) sono rispettivamente lunghezza, larghezza e altezza.
- Sfera $$ V = \frac{4}{3} \pi r^3 $$ dove \( r \) è il raggio della sfera.
- Cilindro $$ V = \frac{ \pi r^2 h }{3} $$ con \( r \) raggio della base e \( h \) altezza del cono.
- Cono $$ V = \pi r^2 h $$ con \( r \) raggio della base e \( h \) altezza del cilindro.
- Piramide $$ V = \frac{A_{base} \cdot h}{3} $$ con \( A_ {base} \) area della base e \( h \) altezza della piramide.
Esempio. Se un cubo ha un lato di 2 metri, il volume è: $$ V = 2^3 = 8 \text{ m}^3 $$ Una sfera con un raggio di 3 metri avrà un volume di: $$ V = \frac{4}{3} \pi (3)^3 \approx 113.1 \text{ m}^3 $$
Multipli e sottomultipli dell'unità di misura del volume
L'unità di misura principale del volume nel Sistema Internazionale (SI) è il metro cubo (\( \text{m}^3 \)), ma esistono vari multipli e sottomultipli utilizzati per comodità in diverse situazioni. Ecco una panoramica:
| Multiplo/Sottomultiplo | Simbolo | Conversione con \( \text{m}^3 \) |
|---|---|---|
| Chilometro cubo | \( \text{km}^3 \) | 1 \( \text{km}^3 \) = \( 10^9 \, \text{m}^3 \) |
| Ettometro cubo | \( \text{hm}^3 \) | 1 \( \text{hm}^3 \) = \( 10^6 \, \text{m}^3 \) |
| Decametro cubo | \( \text{dam}^3 \) | 1 \( \text{dam}^3 \) = \( 10^3 \, \text{m}^3 \) |
| Metro cubo | \( \text{m}^3 \) | 1 \( \text{m}^3 \) |
| Decimetro cubo | \( \text{dm}^3 \) | 1 \( \text{dm}^3 \) = \( 10^{-3} \, \text{m}^3 \) |
| Centimetro cubo | \( \text{cm}^3 \) | 1 \( \text{cm}^3 \) = \( 10^{-6} \, \text{m}^3 \) |
| Millimetro cubo | \( \text{mm}^3 \) | 1 \( \text{mm}^3 \) = \( 10^{-9} \, \text{m}^3 \) |
I sottomultipli sono utilizzati per misurare volumi più piccoli rispetto al metro cubo. I più comuni sono:
Ad esempio, un decimetro cubo (\( \text{dm}^3 \)) è uguale a \( 0.001 \, \text{m}^3 \) e corrisponde a 1 litro (L).
$$ 1 \, \text{dm}^3 = 10^{-3} \, \text{m}^3 $$
Un centimetro cubo (\( \text{cm}^3 \)) è uguale a \( 0.000001 \, \text{m}^3 \) e corrisponde a 1 millilitro (mL).
$$ 1 \, \text{cm}^3 = 10^{-6} \, \text{m}^3 $$
I multipli sono, invece, usati per misurare volumi molto più grandi rispetto al metro cubo. I più comuni sono:
Ad esempio, un decametro cubo (\( \text{dam}^3 \)) è uguale a 1000 metri cubi.
$$ 1 \, \text{dam}^3 = 10^3 \, \text{m}^3 $$
Il fattore di conversione
Il fattore di conversione del volume tra i vari multipli e sottomultipli segue il principio del cubo, dato che il volume è una misura tridimensionale composta dal prodotto di tre lunghezze.
Di conseguenza, ogni passaggio tra le unità di volume comporta un fattore \( 10^3 \).
In altre parole, quando passo da un'unità di lunghezza all'unità di volume, si eleva al cubo il rapporto.
Ad esempio, se passo da metri a decimetri devo moltiplicare per \( 10^3 \) perché 1 metro = 10 decimetri per la lunghezza, la larghezza e la profondità dell'oggetto. Di conseguenza
$$ 1 \, \text{m}^3 = 10 \ \text{dm} \times 10 \ \text{dm} \times 10 \ \text{dm} = (10 \ \text{dm})^3 = 1000 \, \text{dm}^3 $$
Questa regola si applica a tutte le unità di volume, per cui ogni cambio di scala comporta la moltiplicazione o la divisione per \( 10^3 \). Ecco come funziona:
| Passaggio | Fattore di Conversione |
|---|---|
| da km³ a hm³ | \( 10^3 \) |
| da hm³ a dam³ | \( 10^3 \) |
| da dam³ a m³ | \( 10^3 \) |
| da m³ a dm³ | \( 10^3 \) |
| da dm³ a cm³ | \( 10^3 \) |
| da cm³ a mm³ | \( 10^3 \) |
Ad esempio, se vogliamo convertire 1 metro cubo (\( \text{m}^3 \)) in centimetri cubi (\( \text{cm}^3 \)):
Devo considerare che 1 metro = 100 centimetri.
$$ 1 \, \text{m}^3 = (100 \, \text{cm})^3 = 1 \ 000 \ 000 \, \text{cm}^3 = 10^6 \, \text{cm}^3 $$
Questo principio è valido per tutte le conversioni, rendendo le unità di volume facili da scalare seguendo questa regola base.
Un esempio pratico di conversione più complesso. Devo convertire 7 hm3 (ettometri cubi) in cm3 (centimetri cubi). Per farlo scrivo un'equivalenza dove $ x $ è una variabile incognita. $$ 7 \ \text{hm}^3 = x \ \text{cm}^3 $$ Sostituisco l'ettometro (hm) con la relativa potenza in base dieci 102m e il centimetro (cm) con 10-2. $$ 7 \cdot (10^2)^3 = x \cdot (10^{-2})^3 $$ Poi svolgo il calcolo algebrico tra le potenze e ricavo il valore dell'incognita x.$$ 7 \cdot 10^6 = x \cdot 10^{-6} $$ $$ x = \frac{ 7 \cdot 10^6}{ 10^{-6}} $$ $$ x = 7 \cdot 10^{6-(-6)}$$ $$ x = 7 \cdot 10^12 $$ Una volta ottenuto il valore dell'incognita, lo sostituisco nell'equivalenza iniziale. $$ 7 \ \text{hm}^3 = x \ \text{cm}^3 $$ $$ 7 \ \text{hm}^3 = 7 \cdot 10^{12} \ \text{cm}^3 $$ Ho così ottenuto la conversione da ettolitri cubi in centimetri cubi. Questa procedura è generale e mi permette di passare da un multiplo a un sottomultiplo o viceversa. E' però necessario conoscere il calcolo algebrico tra le potenze.
In alternativa, posso contare gli spostamenti della virgola per passare da un multiplo a un sottomultiplo (o viceversa) e contare ogni spostamento come un prodotto o una divisione per una potenza di 103.
- Se passo da un multiplo a un sottomultiplo moltiplico per 103 ogni spostamento della virgola verso sinistra.
- Se passo da un sottomultiplo a un multiplo divido per 103 ogni spostamento della virgola verso sinistra.
Esempio. Per convertire 7 hm3 (ettometri cubi) in cm3 (centimetri cubi). Per passare dagli ettometri (hm) ai centrimetri (cm) sono necessari 4 spostamenti della virgola verso destra.
- Da hm (ettometri) a dam (decametri)
- Da dam (decametri) a m (metri)
- Da m (metri) a dm (decimetri)
- Da dm (decimetri) a cm (centimetri)
Il litro
Oltre ai multipli e sottomultipli del metro cubo, esistono altre unità di misura del volume comunemente utilizzate. Ad esempio, è molto diffuso il litro (L) per misurare il volume di un liquido.
Un litro è pari a 1 decimetro cubo
$$ 1 \, \text{L} = 1 \, \text{dm}^3 $$
Spesso si usano anche i sottomultipli come il millilitro (mL), dove:
$$ 1 \, \text{mL} = 1 \, \text{cm}^3 = 0.001 \, \text{L} $$
E così via.
