La media ponderata
La media è detta media ponderata quando i termini sono moltiplicati per un peso. Si ottiene tramite il rapporto tra la somma dei prodotti dei numeri per i loro pesi e la somma dei pesi stessi. $$ \mu = \frac{ x_1 p_1 + x_2 p_2 + ... + x_n p_n }{ p_1 + p_2 + ... + p_n } $$ Dove x1, x2, ... , xn sono i valori mentre p1, p2, ... , pn sono i loro pesi.
La media ponderata si distingue dalla media semplice, in cui i termini concorrono direttamente al calcolo della media, senza alcun peso.
Esistono diverse medie ponderate
- La media aritmetica ponderata
- La media geometrica ponderata
- La media armonica ponderata
- La media quadratica ponderata
Quando i pesi p1, p2, ... , pn sono usati per indicare le frequenze, la media ponderata si riduce a una media ordinaria, solo espressa in modo diverso.
Tuttavia, se i pesi riflettono un'importanza soggettiva o altre variabili, la media ponderata consente di ottenere un risultato che tiene conto di tali differenze.
Ad esempio, se un esame universitario si basa su un compito scritto e un orale potrei usare la media ponderata per dare un peso maggiore al voto dello scritto, invece di calcolare la media aritmetica.
Un esempio pratico
Ecco un esempio pratico di media aritmetica ponderata
Considero questa tabella di dati che mostra i risultati di una sessione d'esame.
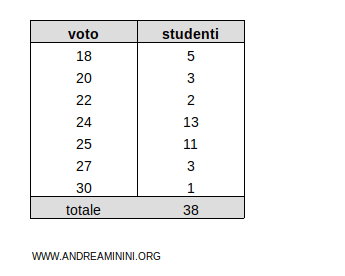
Le stesse modalità (i voti) concorrono più volte al calcolo della media, perché più studenti ottengono lo stesso voto.
Nota. Ad esempio, cinque studenti hanno preso 18, tre studenti hanno preso 20, due studenti hanno preso 22, e via dicendo.
In questo caso i termini del fenomeno sono i voti mentre i pesi sono gli studenti (frequenze assolute)
Per calcolare la media ponderata aritmetica utilizzo questa formula
$$ \mu = \frac{\sum_{i=1}^k x_i \cdot p_i }{ \sum_{i=1}^k p_i } $$
Dove x sono i termini (voti) e p sono i pesi o frequenze (numero di studenti).
La media aritmetica ponderata è il rapporto tra la somma dei prodotti xn per la somma dei pesi.
$$ \mu = \frac{18 \cdot 5 + 20 \cdot 3 + 22 \cdot 2 + 24 \cdot 13 + 25 \cdot 11 + 27 \cdot 3 + 30 \cdot 1}{5+3+2+13+11+3+1} $$
$$ \mu = \frac{90 + 60 + 44 + 312 + 275 + 81 + 30}{38} $$
$$ \mu = \frac{892}{38} $$
$$ \mu = 23,47 $$
Pertanto, la media aritmetica ponderata della distribuzione è μ=23,47
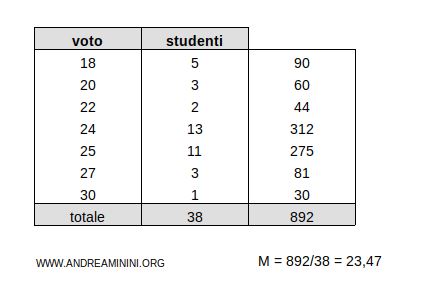
In questo esempio i pesi sono le frequenze.
Quindi, il risultato è lo stesso che otterrei calcolando la media aritmetica di tutti i voti degli studenti.
Esempio 2
Ecco un esempio di calcolo della media ponderata con una tabella che mostra i voti di uno studente per un esame scritto e orale.
In questo caso, il voto dello scritto ha un peso doppio rispetto a quello dell'orale.
| Esame | Voto | Peso |
|---|---|---|
| Scritto | 28 | 2 |
| Orale | 24 | 1 |
Per calcolare la media ponderata, uso la seguente formula:
$$ \text{Media Ponderata} = \frac{\sum (voto \times peso)}{\sum pesi} $$
In questo caso il voto dello scritto è 28 e ha un peso uguale a 2, mentre il voto dell'orale è 24 e ha un peso uguale a 1.
$$ \text{Media Ponderata} = \frac{(28 \times 2) + (24 \times 1)}{2 + 1} = \frac{56 + 24}{3} = \frac{80}{3} \approx 26.67 $$
Quindi, la media ponderata dell'esame tenendo conto dei pesi è circa 26.67.
In questo esempio i pesi sono soggettivi, dipendono dall'obiettivo che voglio raggiungere. In questo caso, voglio dare un peso maggiore al voto dello scritto.
Nota. Se avessi calcolato la media aritmetica il risultato finale sarebbe stato 26. La media aritmetica è una media ponderata in cui tutti i valori hanno lo stesso peso. Ad esempio, un peso unitario per ogni valore.
E così via
