La moda statistica

Cos'è la moda

In statistica la moda di una distribuzione X è la modalità che si presenta più volte, ossia quella con la maggiore frequenza.

La moda è anche detta valore normale, valore modale o norma. In pratica, indica il valore più presente nella distribuzione.

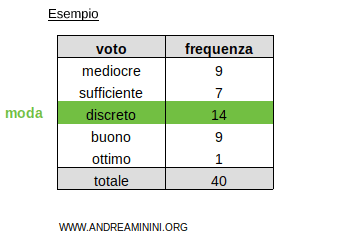
Ad esempio, in questa tabella la moda è il voto "discreto" perché ha la frequenza più alta (14).

E' uno degli indici sintetici di posizione di una distribuzione insieme alla media e alla mediana.

La classe modale

E' possibile calcolare la moda anche nelle distribuzioni di frequenze. In questo caso i valori sono raggruppati in classi.

In una distribuzione di frequenze la moda è la classe con la frequenza maggiore ed è detta classe modale.

Ad esempio, in questa tabella la classe 23-25 è la classe modale perché ha la frequenza più alta (14) rispetto alle altre classi.

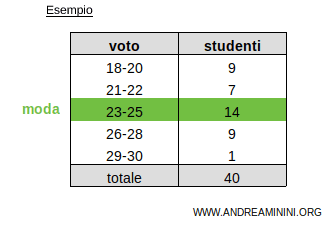
Quando le classi hanno ampiezze diverse, come in questo caso, per calcolare la moda è meglio dividere la frequenza per l'ampiezza della classe.

Il rapporto tra la frequenza e l'ampiezza della classe è anche detto densità di frequenza.

La classe modale è la classe con il rapporto maggiore.

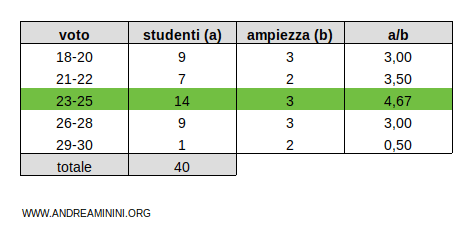
Spiegazione. Ad esempio, la classe 23-25 ha un'ampiezza pari a 3 perché è composta da 23,24 e 25 e una frequenza uguale a 14. Pertanto, il rapporto frequenza/ampiezza (densità di frequenza) è 14/3 = 4,67. E' il rapporto più alto tra tutte. Quindi, la classe 23-25 è la classe modale.

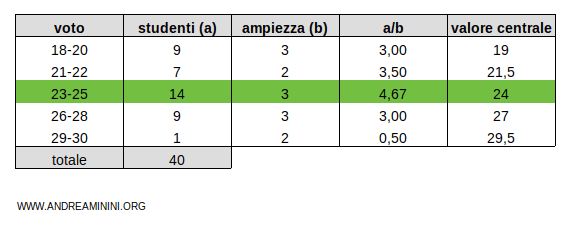
Per calcolare il valore modale della classe modale posso ricorrere all'interpolazione lineare o semplicemente al valore centrale della classe.

Ad esempio, il valore centrale della classe modale 23-25 è 24. Pertanto, il valore modale è 24.

Quindi per calcolare la classe modale:

• Se le classi hanno la stessa ampiezza, la classe modale è quella con la frequenza maggiore.
• Se le classi non hanno la stessa ampiezza, la classe modale è quella con la densità di frequenza maggiore, ossia quella con il maggiore rapporto tra la frequenza e l'ampiezza della classe.

Un esempio pratico

Considero la distribuzione

$$ X = \{ 1,2,5,2,6,7,3,3,2 \} $$

Il termine 2 si ripete tre volte nella distruzione.

E' il termine con maggiore frequenza.

$$ X = \{ 1, \color{red}2,5,\color{red}2,6,7,3,3,\color{red}2 \} $$

Pertanto, la moda della distribuzione è uguale a 2.

$$ \mu_o = 2 $$

Essendoci una sola moda, la distribuzione è unimodale.

Esempio 2

Considero la distribuzione

$$ X = \{ 1,2,3,4,5,6,7,8,9 \} $$

In questo caso la distribuzione non ha una moda perché tutti i termini hanno la stessa frequenza pari a uno.

E' un esempio pratico di distribuzione zeromodale.

Esempio 3

Considero la distribuzione di frequenze

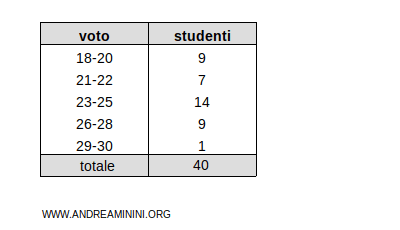
In questo caso, la moda è la classe 23-25 perché è la classe con frequenza maggiore (14).

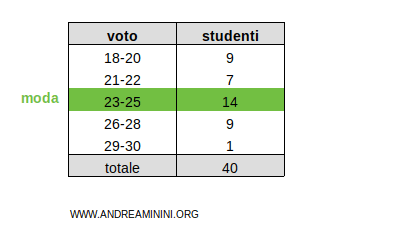
Osservazioni

Alcune osservazioni sulla moda

• La moda è l'unico indice di sintesi della posizione che può essere calcolato sulle distribuzioni qualitative non ordinabili oltre che sulle distribuzioni quantitative.

  Esempio. Questa distribuzione ha modalità qualitative non ordinabili. Perché i colori sono una qualità non ordinabile. In questo caso non è possibile calcolare la media o la mediana.
  
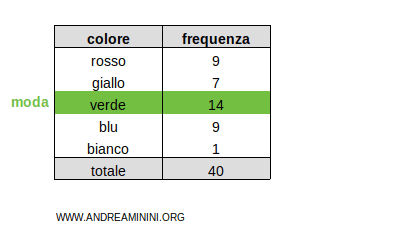
  E' però possibile trovare la moda. La moda della distribuzione è la classe con maggiore frequenza (14) ossia la classe verde.

• Nelle distribuzioni in scala continua la moda è il valore x in cui la densità f(x) raggiunge il valore massimo.
• In una curva di distribuzione la moda è il punto di massimo del grafico. Se la distribuzione è unimodale c'è un solo punto di massimo. Viceversa, se la distribuzione è plurimodale ci sono più punti di massimo.
  
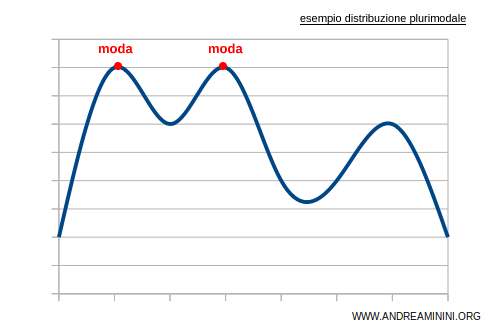
• In una curva di distribuzione di frequenze normale (unimodale e simmetrica) la moda, la media e la mediana sono uguali.
  

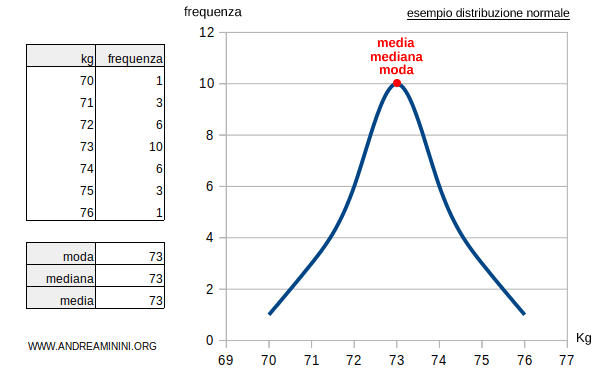
  Altro esempio. Considero una semplice distribuzione di valori simmetrica composta da n=9 termini $$ X = \{\ 1,2,3,4,4,4,5,6,7 \}$$ La moda è uguale a 4 perché quattro è il termine che si ripete più volte $$ \mu_o=4 $$ Anche la media aritmetica è uguale a 4. $$ \mu = \frac{1+2+3+4+4+4+5+6+7}{9} = \frac{36}{9} = 4 $$ Infine, anche la mediana è uguale a 4 $$ \mu_e = 4 $$ Tutti gli indici coincidono.

• Se la distribuzione è asimmetrica la moda, la media e la mediana hanno valori diversi.
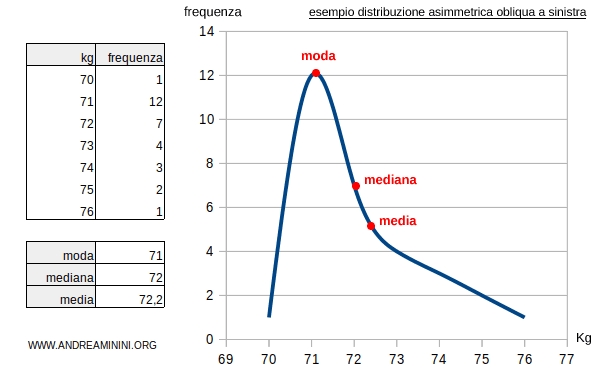
  • Se la distribuzione di frequenze è asimmetrica e obliqua a sinistra la moda è inferiore alla mediana e alla media. $$ \mu_o < \mu_e < \mu $$ Esempio
    
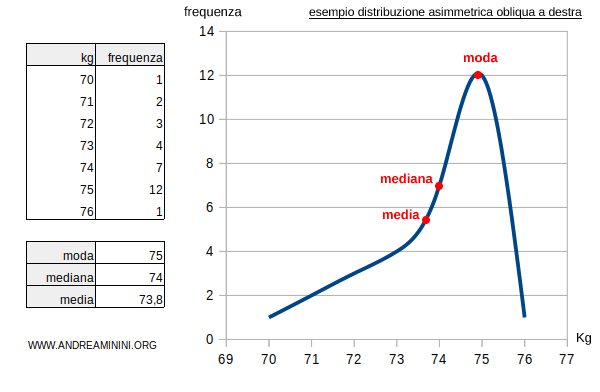
  • Se la distribuzione di frequenze e asimmetrica e obliqua a destra la moda è superiore alla mediana e alla media. $$ \mu < \mu_e < \mu_o $$ Esempio
    

E così via.