La media geometrica
La media geometrica è la radice ennesima del prodotto di n termini. $$ \mu_g = \sqrt[n]{x_1 \cdot x_2 \cdot x_3 \cdot x_4 \cdot ... \cdot x_n } = \sqrt[n]{ \prod_{i=1}^n x_i} $$
A cosa serve
La media geometrica è un indice sintetico di posizione come la media aritmetica.
Tuttavia, non restituisce lo stesso risultato della media aritmetica.
Quando usare la media geometrica. La media geometrica è utile per alcune sue proprietà. In particolar modo per il calcolo del valore medio del rapporto di due serie Xi/Yi. Si presta al calcolo della media dei tassi e di tutte le grandezze che per loro natura sono moltiplicate tra loro. E' molto più sensibile ai valori molto piccoli rispetto alla media aritmetica. Tuttavia, non può essere usata se almeno uno dei valori uguale a zero oppure è negativo.
A differenza della media aritmetica, la media geometrica tiene conto dell'effetto cumulativo dei tassi di variazione.
Questo la rende particolarmente adatta per calcolare tassi di crescita medi nel tempo, come nel caso dell'inflazione, della crescita demografica o dei rendimenti finanziari.
In questi casi, utilizzando la media geometrica, si ottiene una misura più accurata della variazione complessiva di un fenomeno nel tempo.
Un esempio pratico
Considero questa distribuzione di dati composta da n=5 termini
$$ X = \{ 1 , 2, 3 , 4 , 5 \} $$
La media geometrica della distribuzione è
$$ \mu_g = \sqrt[5]{ 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 } $$
$$ \mu_g = \sqrt[5]{ 120 } $$
$$ \mu_g = 2,6 $$
La media geometrica della distribuzione X è circa 2,6
La media geometrica non coincide con la media aritmetica. In questo esempio la media aritmetica della distribuzione X è uguale a 3.
$$ \mu = \frac{1+2+3+4+5}{5} = \frac{15}{5} = 3 $$
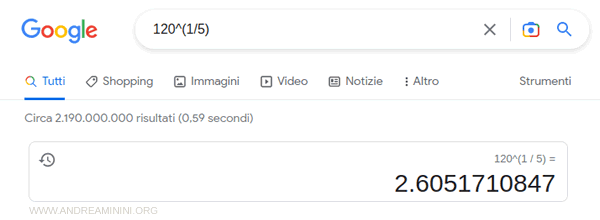
Nota. Per calcolare la radice ennesima al computer applico la proprietà invariantiva dei radicali ed elevo il radicando al reciproco dell'indice della radice $$ \mu_g = \sqrt[5]{ 120 } = 120^{1/5} = 2,6 $$ Ad esempio, per calcolarla su Google digito 120^{1/5} nel campo delle ricerche e premo invio.
Esempio 2
Ecco un esempio pratico dell'utilizzo della media geometrica con i tassi di variazione.
Devo calcolare il tasso medio di un investimento.
Supponiamo di aver investito una somma di denaro che ha subito i seguenti tassi di rendimento annuali nel corso di tre anni:
- Anno 1: +20% di rendimento
- Anno 2: -10% di rendimento
- Anno 3: +15% di rendimento
Voglio determinare il tasso di crescita medio annuo dell'investimento utilizzando la media geometrica.
Per calcolare la media geometrica, devo prima trasformare i tassi percentuali in fattori di crescita moltiplicativi.
- Anno 1: \( 1 + 0,20 = 1,20 \)
- Anno 2: \( 1 - 0,10 = 0,90 \)
- Anno 3: \( 1 + 0,15 = 1,15 \)
Moltiplico i fattori di crescita tra loro:
$$ \text{Prodotto} = 1,20 \times 0,90 \times 1,15 = 1,242 $$
La media geometrica è la radice n-esima (dove n è il numero di periodi) del prodotto dei fattori di crescita.
$$ \text{Media Geometrica} = \sqrt[3]{1,242} \approx 1,075 $$
Infine, converto la media geometrica in tasso percentuale. Sottraggo 1 e moltiplico per 100 per ottenere il tasso percentuale medio:
$$ \text{Tasso di crescita medio annuo} = (1,075 - 1) \times 100\% = 7,5\% $$
In base alla media geometrica il tasso di crescita medio annuo dell'investimento è del 7,5%
Perché usare la media geometrica? Questo metodo tiene conto dell'effetto cumulativo dei tassi di variazione, riflettendo accuratamente come l'investimento si è evoluto nel tempo. Se avessi utilizzato la media aritmetica, il calcolo sarebbe stato un tasso medio dell'8,33%. $$ \text{Media Aritmetica} = \frac{(+20\% - 10\% + 15\%)}{3} = \frac{25\%}{3} \approx 8,33\% $$ Questo accade perché la media aritmetica non considera l'effetto compounding e può sovrastimare il rendimento reale. Utilizzando la media geometrica, invece, ottengo una misura più accurata del tasso di crescita medio annuo quando si hanno tassi di variazione che si applicano in modo sequenziale nel tempo. La media geometrica è particolarmente utile quando i valori sono dipendenti l'uno dall'altro nel tempo, come nel caso dei rendimenti di un investimento, dove il rendimento di un anno influenza la base su cui si calcola il rendimento dell'anno successivo.
La differenza tra la media geometrica e aritmetica
La media geometrica è molto più sensibile alla presenza dei valori molto piccoli rispetto alla media aritmetica.
Inoltre, se anche un solo termine della distribuzione è uguale a zero, la media geometrica si annulla del tutto. Lo stesso non accade nella media aritmetica.
Esempio
Considero questa distribuzione X di valori
$$ X = \{ 100, 200, 300, 400, 0.1 \} $$
La media aritmetica di X è uguale a 200,02
$$ \mu = \frac{100+200+300+400+0.1}{5} = \frac{1000.1}{5} = 200.02 $$
La media geometrica di X è uguale a 47,42
$$ \mu_g = \sqrt[5]{ 100 \cdot 200 \cdot 300 \cdot 400 \cdot 0.1 } = \sqrt[5]{240000000 } = 47.42 $$
La differenza del valore medio è notevole.
Esempio 2
Il prezzo di un prodotto è 50 ∈ a inizio 2019.
Nel 2019 e nel 2020 il prezzo cresce del 1%. Nel 2021 il prezzo si impenna con un incremento del 90% raggiungendo il prezzo finale di 96,91 € nel 2022.
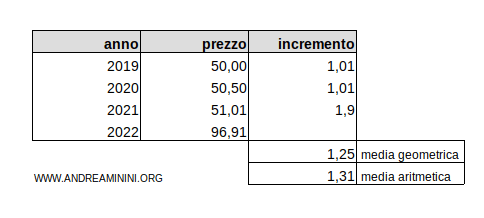
La media geometrica dei tassi nel triennio è del 25%
$$ \mu_g = \sqrt[3]{1,01 \cdot 1,01 \cdot 1,9} = \sqrt[3]{ 1.93819 } = 1,25 $$
La media aritmetica dei tassi nel triennio è del 31%
$$ \mu = \frac{1,01 + 1,01 + 1,9}{3} = \frac{3,92}{3} = 1,31 $$
Quale delle due medie è più accurata?
Per saperlo basta fare una simulazione.
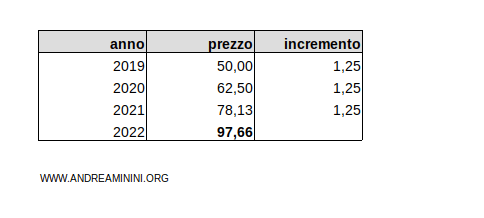
Se applico il tasso medio annuo del 25% (ossia 1,25) calcolato con la media geometrica ottengo un prezzo finale pari a 50·1,253=97,6 €
Se applico il tasso medio annuo del 31% (ossia 1,31) calcolato con la media aritmetica ottengo un prezzo finale pari a 50·1,313=112,4 €
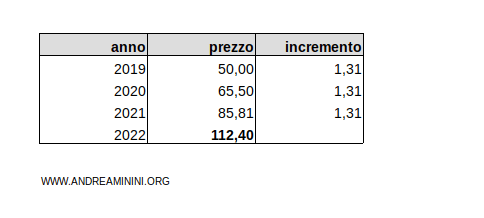
Il prezzo che si avvicina di più al prezzo reale del bene (96,91 €) nel 2022 è quello calcolato con la media geometrica (97,6 €)
Pertanto, in questo caso la media geometrica è più accurata.
Osservazioni
Alcune osservazioni sulla media geometrica
- La media geometrica del rapporto tra due serie Xi/Yi è uguale al rapporto delle medie geometriche delle due serie $$ \mu_g ( \frac{X_i}{Y_i} ) = \frac{\mu_g (X)}{\mu_g(Y)} $$ Per questa ragione la media geometrica si presta al calcolo del valore medio del rapporto di due serie. Ad esempio, questa proprietà non è soddisfatta dalla media aritmetica.
- La media geometrica non può essere calcolata se uno dei termini della distribuzione è uguale a zero, perché il prodotto dei termini è nullo.
- La media geometrica non può essere calcolata se ci sono valori negativi nella distribuzione, perché una radice con indice pari non ha soluzioni reali se il radicando negativo.
- La media geometrica è molto più sensibile ai valori molto piccoli, purché non nulli, perché il prodotto si riduce notevolmente se uno dei fattori è molto piccolo. Lo stesso non accade nella media aritmetica.
- La media geometrica è uguale alla media aritmetica quando i termini di una distribuzione sono tutti uguali tra loro.
- La media geometrica si può calcolare anche usando una formula con gli esponenziali e i logaritmi naturali. Il risultato è lo stesso. $$ \mu_g = e^{ \ \frac{1}{n} \cdot \sum_{i=1}^n \ln x_i \ } $$
Esempio. Considero questa distribuzione di dati composta da n=5 termini $$ X = \{ 1 , 2, 3 , 4 , 5 \} $$ La media dei logaritmi naturali dei termini è uguale a 0,96 $$ \frac{\ln(1) + \ln(2) + \ln(3)+ \ln(4) + \ln(5)}{5} = \frac{4,79}{5} = 0,96 $$ L'esponenziale di 0,96 è circa 2,6 $$ e^{0,96} = 2,6 $$ E' lo stesso risultato ottenuto nell'esempio precedente.
- La media geometrica ponderata
La media geometrica ponderata è una versione alternativa della media geometrica semplice in cui a ogni termine è associato un peso arbitrario (wi). $$ \mu = \sqrt[ \sum{w_i} \ ]{\prod_{i=1}^n x_i^{w_i} } $$
E così via.
