La mediana

La mediana è il valore centrale che divide una distribuzione ordinata in due gruppi di uguale numerosità.

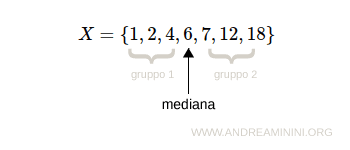
Il primo gruppo è composto dai termini minori o uguali alla mediana.

Il secondo gruppo è, invece, composto dai termini maggiori o uguali alla mediana.

Come trovare la mediana

Per prima cosa ordino la distribuzione in modo crescente.

Poi calcolo la posizione mediana a seconda se la distribuzione ordinata ha un numero pari o dispari di termini

• Se la distribuzione ha un numero n dispari di termini, la mediana è il termine che occupa la posizione centrale (c) $$ c = \frac{n+1}{2} $$

  In questo caso la mediana è il valore del termine x_c della distribuzione ordinata $$ \mu = x_c $$

• Se la distribuzione ha un numero n pari di termini, la mediana è la media aritmetica dei termini che occupano le posizioni centrali c₁ e c₂ $$ c_1 = \frac{n}{2} $$ $$ c_2 = \frac{n}{2} + 1 $$

  In questo caso la mediana è la media dei termini x_c1 e x_c2 della distribuzione ordinata $$ \mu = \frac{x_{c1} + x_{c2} }{2} $$

Un esempio pratico

Considero la distribuzione

$$ X = \{ 4,1,7,2,6,18,12 \} $$

Ordino la distribuzione in modo crescente

$$ X = \{ 1,2,4,6,7,12,18 \} $$

A ogni termine della distribuzione ordinata assegno un indice crescente a partire a 1 che ne individua la posizione

$$ x_1 = 1 \\ x_2=2 \\ x_3 = 4 \\ x_4 = 6 \\ x_5=7 \\ x_6=12 \\ x_7=18 $$

In questo caso la distribuzione ha n=7 elementi

Essendo un numero dispari, per trovare la posizione della mediana nella distribuzione uso la formula

$$ c = \frac{n+1}{2} = \frac{7+1}{2} = \frac{8}{2}=4 $$

La mediana è il termine che occupa la posizione c=4

Pertanto, la mediana è il valore x₄=6

$$ \mu_e = x_c = x_4 = 6 $$

La mediana divide la distribuzione in due gruppi di tre termini.

Esempio 2

Considero la distribuzione

$$ X = \{ 3,8,12,2,6,7,3,18 \} $$

Ordino la distribuzione in modo crescente

$$ X = \{ 2,3,3,6,7,8,12,18 \} $$

A ogni termine della distribuzione ordinata assegno un indice crescente

$$ x_1 = 2 \\ x_2=3 \\ x_3 = 3 \\ x_4 = 6 \\ x_5=7 \\ x_6=8 \\ x_7=12 \\ x_8=18 $$

In questo caso la distribuzione ha n=8 elementi

Essendo un numero pari, per trovare la mediana trovo le due posizioni mediane c₁ e c₂

$$ c_1 = \frac{n}{2} = \frac{8}{2} = 4 $$

$$ c_2 = \frac{n}{2} + 1 = \frac{8}{2} + 1 = 4+1 =5 $$

I rispettivi valori della distribuzione che occupano la quarta (c₁=4) e la quinta (c₂=5) posizione nella distribuzione x sono x₄=6 e x₅=7

$$ x_{c1} = x_4 = 6 $$

$$ x_{c2} =x_5 = 7 $$

La mediana è la media di questi ultimi due termini

$$ \mu_e = \frac{x_{c1}+x_{c2}}{2} = \frac{6+7}{2} = \frac{13}{2} = 6,5 $$

Pertanto, la mediana è uguale a 6,5

$$ \mu_e = 6,5 $$

Nota. Quando la distribuzione ha un numero pari di elementi, la mediana non è detto che sia un termine presente nella distribuzione. Ad esempio, in questo caso il valore mediano 6,5 non è presente nella distribuzione iniziale X={4,1,7,2,6,18,12} .

La mediana in una distribuzione di frequenza

Per calcolare la mediana in una distribuzione di frequenze

1. Calcolo la frequenza assoluta cumulata sommando a ogni frequenza le frequenze precedenti.
2. Individuo la posizione mediana (c) nella frequenza cumulata

   Se la frequenza cumulata è un numero pari la posizione mediana è $$ c = \frac{ \sum_{k=1}^n f_k}{2} $$ Se invece la frequenza cumulata è un numero dispari la posizione mediana è $$ c = \frac{ 1 + \sum_{k=1}^n f_k}{2} $$

3. Verifico in quale frequenza cumulata è compresa la posizione mediana (c)
4. La classe associata alla frequenza cumulata in cui si colloca la posizione mediana è la classe mediana.

Esempio

Considero questa distribuzione di frequenze

Aggiungo un'ulteriore colonna con le frequenze assolute cumulate

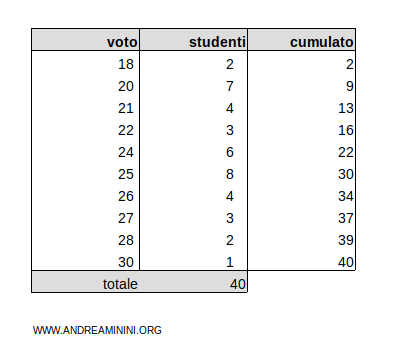
La frequenza cumulata complessiva è 40.

E' un numero pari, quindi ottengo la posizione mediana usando la formula

$$ c = \frac{ \sum_{k=1}^n f_k}{2} = \frac{40}{2} = 20 $$

La posizione mediana è c=20

A questo punto controllo in quale frequenza cumulata si trova la posizione mediana c=20

In questo caso la posizione mediana c=20 si trova nell'intervallo delle frequenze cumulate 16-22 associato alla classe 24

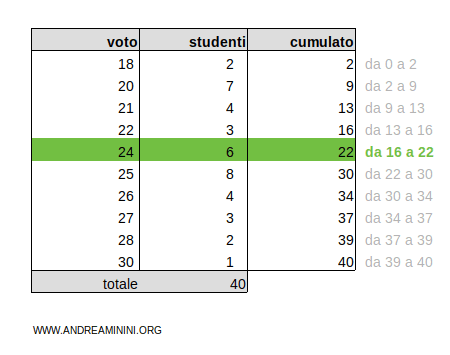
Pertanto, la classe mediana della distribuzione di frequenze è 24.

$$ \mu_e = 24 $$

Esempio 2

Considero questa distribuzione di frequenza ripartita in classi

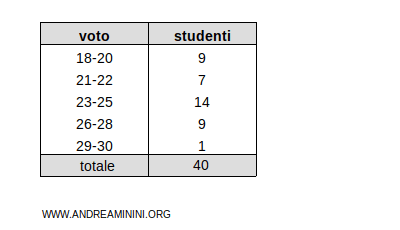
In questo caso ogni classe è un intervallo di valori

Aggiungo un'ulteriore colonna per il cumulato delle frequenze assolute

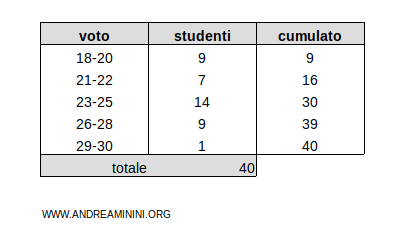
Anche in questo caso a frequenza cumulata complessiva (40) è un numero pari.

Quindi ottengo la posizione mediana usando la formula

$$ c = \frac{ \sum_{k=1}^n f_k}{2} = \frac{40}{2} = 20 $$

La posizione mediana è c=20

La posizione mediana c=20 è collocata nella classe 23-25

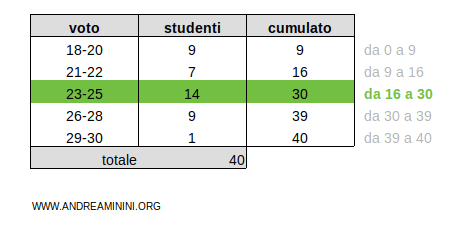
Pertanto la mediana è la classe 23-25.

Per calcolare il valore preciso della mediana utilizzo l'interpolazione lineare nella classe 23-25.

$$ \mu_e = x_{inf} + (x_{sup} - x_{inf}) \cdot \frac{ c - n_{prec} }{n_{classe}} $$

I termini hanno questo significato

• x_inf=23 e x_sup=25 sono gli estremi della classe 23-25
• c=20 è la posizione mediana
• n_classe=14 è la frequenza della classe 23-25.
• n_prec=16 è la frequenza cumulata delle classi precedenti alla classe 23-25

A questo punto sostituisco i valori e svolgo i calcoli

$$ \mu_e = 23 + (25 - 23) \cdot \frac{ 20 - 16 }{14} $$

$$ \mu_e = 23 + 2 \cdot \frac{ 4 }{14} $$

$$ \mu_e = 23 + \frac{4}{7} $$

$$ \mu_e = 23 + 0,57 $$

$$ \mu_e = 23,57 $$

Il valore della mediana è 23,57

Nota. Allo stesso risultato arrivo facendo una proporzione fra i valori delle classi e le frequenze cumulate $$ (25-23):(x-23) = (30-16):(c-16) $$ Dove la posizione mediana è c=20 $$ (25-23):(x-23) = (30-16):(20-16) $$ $$ 2:x-23 = 14:4 $$ Riscrivo la proporzione come frazione $$ \frac{2}{x-23} = \frac{14}{4} $$ Infine, ricavo l'incognita x $$ \frac{2}{\frac{14}{4} } = x-23 $$ $$ 2 \cdot \frac{4}{14} + 23 = x $$ $$ x = \frac{4}{7} + 23 = 23,57 $$ Il risultato finale è lo stesso.

Osservazioni

Alcune osservazioni sulla mediana

• La mediana non è influenzata dai valori estremi molto grandi o molto piccoli e dalla presenza di dati anomali all'interno della distribuzione. Lo stesso non accade nella media aritmetica.

  Esempio. La mediana della distribuzione X={4,1,7,2,6,18,12} è μ_e=6.
  
  Se sostituisco l'ultimo termine 12 con 200, la mediana è sempre uguale a μ_e=6
  

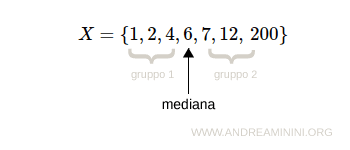
• Somma delle differenze assolute
  La somma delle differenze assolute tra i valori di un insieme e la mediana è minima rispetto a qualsiasi altro valore scelto.

  Esempio. In questo insieme dei dati $$ \{ 1, 2, 4, 6, 7, 12, 18 \} $$ Poiché l'insieme ha un numero dispari di elementi (\(7\)), la mediana è il valore centrale, che è \(6\). Calcolo la somma delle differenze assolute rispetto a \(6\): $$ |1 - 6| + |2 - 6| + |4 - 6| + |6 - 6| + |7 - 6| + |12 - 6| + |18 - 6| $$ $$ 5 + 4 + 2 + 0 + 1 + 6 + 12 = 30 $$ Quindi, la somma delle differenze assolute rispetto alla mediana \(6\) è \(30\). Provo a calcolare la somma delle differenze assolute rispetto a un altro valore, ad esempio \(7\): $$ |1 - 7| + |2 - 7| + |4 - 7| + |6 - 7| + |7 - 7| + |12 - 7| + |18 - 7| $$ $$ 6 + 5 + 3 + 1 + 0 + 5 + 11 = 31 $$ La somma delle differenze assolute rispetto a \(7\) è \(31\), che è maggiore rispetto a quella ottenuta con la mediana (\(30\)). Analogamente, se scegliessi un altro valore diverso dalla mediana, troverei che la somma delle differenze assolute sarebbe sempre maggiore o uguale a quella rispetto alla mediana.

E così via.