Dualità tra un segnale nel tempo e in frequenza
Il valore dello spettro $ X(f) $ in \( f = 0 \) corrisponde all'area del segnale $ x(t) $ nel tempo, e il valore del segnale $ x(t) $ in \( t = 0 \) corrisponde all'area dello spettro $ X(F) $ in frequenza. $$ x(t) |_{t=0} = \int_{-\infty}^{\infty} X(f) \ df $$ $$ X(f) |_{f=0} = \int_{-\infty}^{\infty} x(t) \ dt $$
La dualità tra un segnale \( x(t) \) e la sua trasformata di Fourier \( X(f) \) rivela diverse proprietà simmetriche e reciproche tra il dominio del tempo e quello della frequenza.
Analizzo in dettaglio entrambe queste proprietà.
1] Valore dello spettro in f=0
La trasformata di Fourier di un segnale \( x(t) \) è data da:
$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} \, dt $$
Quando \( f = 0 \) questa diventa:
$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi \cdot 0 \cdot t} \, dt $$
$$ X(f) = \int_{-\infty}^{\infty} x(t) e^0 \, dt $$
Sapendo che $ e^0=1 $
$$ X(0) = \int_{-\infty}^{\infty} x(t) \, dt $$
Quindi, il valore dello spettro \( X(f) \) a \( f = 0 \) è esattamente l'area sottesa dal segnale \( x(t) \) nel dominio del tempo.
Questo valore è chiamato la "componente continua" (DC) del segnale.
2] Valore del segnale in t=0
L'anti-trasformata di Fourier per ottenere \( x(t) \) dal suo spettro \( X(f) \) è data da:
$$ x(t) = \int_{-\infty}^{\infty} X(f) e^{i 2 \pi f t} \, df $$
Quando \( t = 0 \), questa diventa
$$ x(t) = \int_{-\infty}^{\infty} X(f) e^{i 2 \pi f \cdot 0} \, df $$
$$ x(t) = \int_{-\infty}^{\infty} X(f) e^{0} \, df $$
$$ x(t) = \int_{-\infty}^{\infty} X(f) \cdot 1 \, df $$
$$ x(0) = \int_{-\infty}^{\infty} X(f) \, df $$
Quindi, il valore del segnale \( x(t) \) in \( t = 0 \) è dato dall'area sottesa dallo spettro \( X(f) \) nel dominio della frequenza.
Perché accade questa dualità? La dualità tra il dominio del tempo e quello della frequenza deriva dalla struttura matematica della trasformata di Fourier. La presenza dell'integrale in entrambe le trasformate mostra un legame tra il tempo e la frequenza. Il fatto che il valore di \( X(0) \) rappresenti l'area del segnale \( x(t) \) e che \( x(0) \) rappresenti l'area dello spettro \( X(f) \) è una conseguenza della simmetria tra le operazioni di trasformata diretta e inversa di Fourier.
In un certo senso, queste relazioni mostrano come l'energia o l'informazione contenuta nel segnale si possano misurare sia nel dominio del tempo sia nel dominio della frequenza.
Sono un modo alternativo ma equivalente di descrivere e comprendere il segnale.
Un esempio pratico
Considero un segnale rettangolare di ampiezza \( A \) e durata \( T \), centrato in \( t = 0 \).
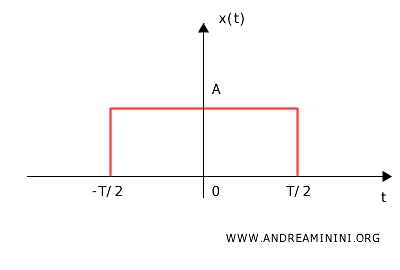
Il segnale \( x(t) \) è definito in questo modo
$$ x(t) =
\begin{cases}
A, & \text{se } -\frac{T}{2} \leq t \leq \frac{T}{2}, \\
0, & \text{altrimenti}.
\end{cases} $$
La trasformata di Fourier di \( x(t) \) è data da:
$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} \, dt $$
L'integrale si calcola solo nell'intervallo \( -\frac{T}{2} \leq t \leq \frac{T}{2} \), dove \( x(t) = A \):
$$ X(f) = \int_{-\frac{T}{2}}^{\frac{T}{2}} A e^{-i 2 \pi f t} \, dt $$
Poiché \( A \) è una costante, posso portarlo fuori dall'integrale:
$$ X(f) = A \int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-i 2 \pi f t} \, dt $$
L'integrale è della forma:
$$ \int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-i 2 \pi f t} \, dt = \left[ \frac{e^{-i 2 \pi f t}}{-i 2 \pi f} \right]_{-\frac{T}{2}}^{\frac{T}{2}} $$
Sostituendo i limiti di integrazione, ottengo:
$$ X(f) = A \left[ \frac{e^{-i 2 \pi f \frac{T}{2}} - e^{i 2 \pi f \frac{T}{2}}}{-i 2 \pi f} \right] $$
Utilizzo l'identità di Eulero \( e^{-i \theta} - e^{i \theta} = -2i \sin(\theta) \), otteniamo:
$$ X(f) = A \frac{-2i \sin\left( \pi f T \right)}{-i 2 \pi f} = A \frac{\sin\left( \pi f T \right)}{\pi f} $$
Quindi, la trasformata di Fourier del segnale rettangolare è:
$$ X(f) = A \frac{\sin\left( \pi f T \right)}{\pi f} $$
Ora applichiamo le proprietà di dualità:
- Valore dello spettro in f=0
Per trovare \( X(0) \), sostituisco \( f = 0 \) nell'espressione della trasformata: $$ X(0) = A \frac{\sin(0)}{0} $$ A prima vista, sembra che sia una forma indefinita \( \frac{0}{0} \). Tuttavia, posso calcolare il limite per \( f \to 0 \): $$ X(0) = \lim_{f \to 0} A \frac{\sin\left( \pi f T \right)}{\pi f} = A T $$ Quindi, il valore dello spettro $ X(0) $ in \( f = 0 \) è pari all'area del segnale rettangolare nel dominio del tempo, cioè \( A T \). $$ X(0) = A T $$ Del resto $ x(t) $ è un segnale rettangolare e l'area di un rettangolo si calcola moltiplicando la base (T) per l'altezza (A).
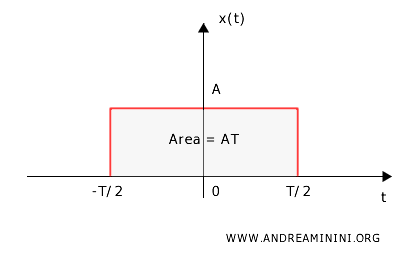
- Valore del segnale in t=0
Il valore del segnale $ x(t) $ in $ t= 0 $ è semplicemente $ A $ $$ x(0) = A $$ Per verificarlo, calcolo l'antitrasformata di Fourier con t=0 $$ x(t) = \int_{-\infty}^{\infty} X(f) e^{i 2 \pi f t} \, dt $$ $$ x(0) = \int_{-\infty}^{\infty} X(f) e^{i 2 \pi f \cdot 0} \, dt $$ $$ x(0) = \int_{-\infty}^{\infty} X(f) e^0 \, dt $$ Sapendo che $ e^0 = 1 $ $$ x(0) = \int_{-\infty}^{\infty} X(f) \cdot 1 \, dt $$ $$ x(0) = \int_{-\infty}^{\infty} X(f) \, dt $$ Quest'ultimo integrale misura l'area dello spettro. Poiché $ x(0)=A $ deduco che l'area dello spettro è uguale ad $ A $ $$ \int_{-\infty}^{\infty} X(f) \, dt = A $$
Nota. Se la funzione integranda è sia positiva che negativa, l'integrale definito non calcola esattamente l'area tra la funzione e l'asse x bensì la somma algebrica delle aree, ovvero l'area positiva meno l'area negativa.
In questo caso il segnale è un segnale rettangolare, quindi la trasformata di Fourier è
$$ X (f) = A T \, \text{sinc}(f T) $$
Dove la funzione sinc (o seno cardinale) è definita come:
$$ \text{sinc}(x) = \frac{\sin(\pi x)}{\pi x} $$
L'integrale di \( X(f) \) diventa:
$$ \int_{-\infty}^{\infty} X(f) \, dt $$
$$ \int_{-\infty}^{\infty} A T \, \text{sinc}(f T) \, df $$
Faccio un cambio di variabile per semplificare l'integrale, ponendo \( u = f T \), da cui \( du = T \, df \) e \( df = \frac{du}{T} \).
$$ \int_{-\infty}^{\infty} A T \, \text{sinc}(f T) \, df $$
$$ A T \int_{-\infty}^{\infty} \text{sinc}(u) \frac{du}{T} $$
Il termine \( T \) si semplifica:
$$ \frac{A T}{T} \int_{-\infty}^{\infty} \text{sinc}(u) \ du $$
$$ A \int_{-\infty}^{\infty} \text{sinc}(u) \, du $$
È noto che l'integrale della funzione sinc è uguale a 1 ovvero $ \int_{-\infty}^{\infty} \text{sinc}(u) \, du = 1 $
$$ A \int_{-\infty}^{\infty} \text{sinc}(u) \, du = A \cdot 1 = A $$
Questo conferma la proprietà di dualità: il valore del segnale al centro (\( x(0) = A \)) corrisponde all'area totale dello spettro.
Anche se la funzione sinc oscilla tra valori positivi e negativi, la compensazione tra le sue parti garantisce che l'integrale risulti pari all'ampiezza \( A \).
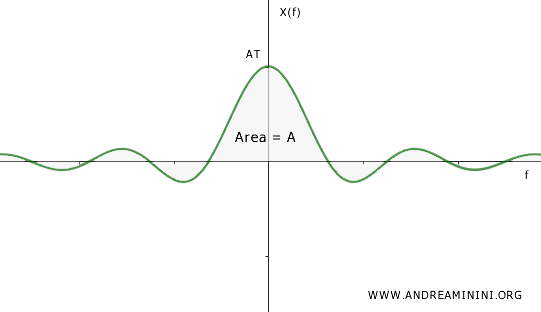
L'esempio del segnale rettangolare mostra chiaramente la dualità tra il dominio del tempo e quello della frequenza.
In questo caso, il valore dello spettro nel punto \( f = 0 \) è uguale all'area totale del segnale nel tempo, mentre il valore del segnale al tempo \( t = 0 \) è uguale all'area dello spettro nel dominio della frequenza.
Questa relazione mette in luce l'equilibrio tra le rappresentazioni temporale e frequenziale dei segnali.
E così via.
