La trasformata di Fourier del seno
La trasformata di Fourier del seno $$ x(t) = \sin(2 \pi f_0 t) $$ è composta da due Delta di Dirac centrate in \( f_0 \) e \( -f_0 \), con un fattore \( \frac{1}{2j} \) e segno opposto: $$ X(f) = \frac{1}{2j} \delta(f - f_0) - \frac{1}{2j} \delta(f + f_0) $$
Considerando anche l'ampiezza \( A \) e la fase \( \phi \).
$$ x(t) = A \sin(2\pi f_0 t + \phi) $$
la trasformata di Fourier è
$$ X(f) = \frac{A}{2j} \left[ e^{j\phi} \delta(f - f_0) - e^{-j\phi} \delta(f + f_0) \right] $$
Dove \( A \) è ampiezza, \( \phi \) è la fase, \( \delta \) è il Delta di Dirac centrato in \( +f_0 \) e \( -f_0 \).
Nel caso particolare in cui \( A = 1 \) e \( \phi = 0 \) si torna al caso iniziale:
$$ X(f) = \frac{1}{2j} \delta(f - f_0) - \frac{1}{2j} \delta(f + f_0) $$
La trasformata del seno ha termini immaginari puri e con segno opposto, a differenza della trasformata del coseno che ha termini positivi e reali.
Nota. In altre parole, il seno produce spettri complessi puramente immaginari centrati in \( f_0 \) e \( -f_0 \), a differenza del coseno, che produce spettri reali. Inoltre, lo spettro del seno è antisimmetrico mentre quello del coseno è simmetrico.
La spiegazione
La trasformata di Fourier della funzione trigonometrica del seno nel dominio del tempo
$$ x(t) = \sin(2 \pi f_0 t) $$
si calcola risolvendo l'integrale di Fourier
$$ X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2 \pi f t} \, dt $$
Tuttavia, è molto più semplice utilizzare la rappresentazione del seno tramite esponenziali complesse, sfruttando la formula di Eulero:
$$ x(t) = \sin(2 \pi f_0 t) = \frac{e^{j 2 \pi f_0 t} - e^{-j 2 \pi f_0 t}}{2j} $$
Quindi, posso riscrivere \( x(t) = \sin(2 \pi f_0 t) \) come:
$$ x(t) = \frac{1}{2j} e^{j 2 \pi f_0 t} - \frac{1}{2j} e^{-j 2 \pi f_0 t} $$
Ora, calcolo la trasformata di Fourier di ciascun termine separatamente:
$$ X(f) = F \left[ \frac{1}{2j} e^{j 2 \pi f_0 t} - \frac{1}{2j} e^{-j 2 \pi f_0 t} \right] $$
Grazie alla linearità della trasformata di Fourier, posso scrivere
$$ X(f) = \frac{1}{2j} \cdot F \left[ e^{j 2 \pi f_0 t} \right] - \frac{1}{2j} \cdot F \left[ e^{-j 2 \pi f_0 t} \right] $$
Dalle trasformate note di Fourier, so già che:
- La trasformata di \( e^{j 2 \pi f_0 t} \) è un impulso a \( f = f_0 \),
- La trasformata di \( e^{-j 2 \pi f_0 t} \) è un impulso a \( f = -f_0 \).
Pertanto, sostituendo questi risultati ottengo la trasformata di Fourier di \( x(t) = \sin(2 \pi f_0 t) \) come:
$$ X(f) = \frac{1}{2j} \delta(f - f_0) - \frac{1}{2j} \delta(f + f_0) $$
Quindi, la trasformata di Fourier del seno è espressa come la differenza di due impulsi situati alle frequenze \( \pm f_0 \), con un fattore immaginario \( \frac{1}{2j} \), che riflette la natura sinusoidale.
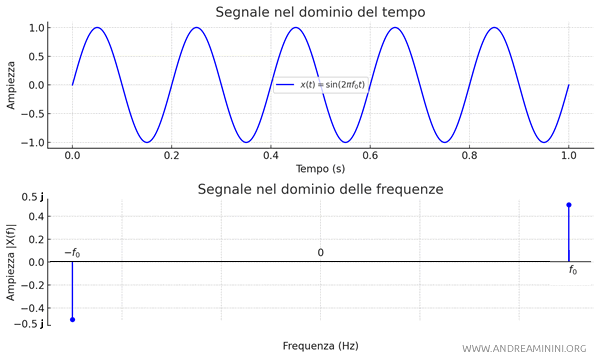
Questa espressione mostra come l'energia del seno si concentra a frequenze \( \pm f_0 \) nel dominio delle frequenze, ma con una fase differente rispetto al coseno.
Nota. La funzione seno nel tempo è una funzione reale e dispari, la sua trasformata in frequenza è una funzione immaginaria pura e dispari, come prevede una delle principali proprietà della trasformata di Fourier.
E così via.
