Teorema della trasformata di Fourier dei segnali reali e dispari

Se $ x(t) $ è una funzione reale e dispari, allora la sua trasformata di Fourier $ X(f) $ è una funzione immaginaria pura e dispari.

Questa è una proprietà fondamentale delle trasformate di Fourier quando vengono applicate a segnali con simmetria rispetto all'origine (disparità) e con valori reali.

Le condizioni da soddisfare sono le seguenti:

• Segnale reale: Un segnale \( x(t) \) è reale se \( x(t) = \overline{x(t)} \), dove \( \overline{x(t)} \) è il complesso coniugato di \( x(t) \). In pratica, questo significa che la funzione non ha componenti immaginarie.
• Segnale dispari: Un segnale è dispari se \( x(-t) = -x(t) \) ovvero \( x(t) = -x(-t) \). Questa simmetria intorno all'origine implica che i valori di \( x(t) \) su un lato del tempo sono esattamente l'opposto dei valori sull'altro lato.

Considero ora la trasformata di Fourier \( X(f) \) di \( x(t) \) nel dominio del tempo:

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt $$

Per un segnale dispari, si può dimostrare che la sua trasformata di Fourier \( X(f) \) è anch'essa una funzione dispari, ovvero:

$$ X(-f) = -X(f)  $$

Inoltre, dato che \( x(t) \) è reale, la trasformata \( X(f) \) non contiene componenti reali ma solo componenti immaginarie. Di conseguenza, \( X(f) \) è una funzione immaginaria pura e dispari.

Questa proprietà è generale e si applica a qualsiasi segnale che soddisfi le condizioni di essere sia reale che dispari. E' una delle proprietà simmetriche della trasformata di Fourier.

Un esempio pratico

Ecco un esempio pratico per illustrare il teorema delle funzioni reali e dispari.

Considero un segnale rettangolare definito come:

$$ x(t) =
\begin{cases}
1, & \text{se } -1 \leq t < 0 \\
-1, & \text{se } 0 \leq t \leq 1 \\
0, & \text{altrimenti}
\end{cases} $$

Questo segnale è sia reale (non ha componenti immaginarie) che dispari (cioè, \( x(t) = -x(-t) \)).

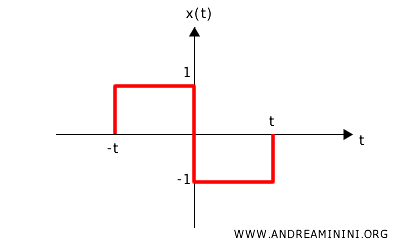
La trasformata di Fourier di \( x(t) \) è:

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt $$

Restringo l'integrazione al dominio della funzione, eliminando tutti gli intervalli in cui si annulla.

Il risultato è la somma di due integrali negli intervalli [-1,0) e [0,1] della retta reale.

$$ X(f) = \int_{-1}^{0} x(t) \cdot e^{-i 2 \pi f t} dt + \int_{0}^{1} x(t) \cdot e^{-i 2 \pi f t} dt $$

Sapendo che x(1)=1 nell'intervallo [-1,0) e che x(t)=-1 nell'intervallo [0,1].

$$ X(f) = \int_{-1}^{0} 1 \cdot e^{-i 2 \pi f t} dt + \int_{0}^{1} (-1) \cdot e^{-i 2 \pi f t} dt $$

Calcolao questi integrali:

• Primo integrale (\( -1 \leq t < 0 \)): $$ \int_{-1}^{0} e^{-i 2 \pi f t} dt = \left[ \frac{e^{-i 2 \pi f t}}{-i 2 \pi f} \right]_{-1}^{0} = \frac{1 - e^{i 2 \pi f}}{-i 2 \pi f} $$
• Secondo integrale (\( 0 \leq t \leq 1 \)): $$ \int_{0}^{1} -e^{-i 2 \pi f t} dt = -\left[ \frac{e^{-i 2 \pi f t}}{-i 2 \pi f} \right]_{0}^{1} = \frac{e^{-i 2 \pi f} - 1}{i 2 \pi f} $$

Sommo i due integrali tra loro

$$ X(f) = \frac{1 - e^{i 2 \pi f}}{-i 2 \pi f} + \frac{e^{-i 2 \pi f} - 1}{i 2 \pi f} $$

Moltiplico e divido il primo termine per -1

$$ X(f) = \frac{1 - e^{i 2 \pi f}}{-i 2 \pi f} \cdot \frac{-1}{-1} + \frac{e^{-i 2 \pi f} - 1}{i 2 \pi f} $$

$$ X(f) = \frac{e^{i 2 \pi f}-1}{i 2 \pi f}  + \frac{e^{-i 2 \pi f} - 1}{i 2 \pi f} $$

Scrivo i termini dell'espressione separatamente per mettere in evidenza quelli da semplificare:

$$ X(f) = \frac{e^{i 2 \pi f}}{i 2 \pi f} - \frac{1}{i 2 \pi f}  + \frac{e^{-i 2 \pi f}}{i 2 \pi f} - \frac{1}{i 2 \pi f} $$

$$ X(f) = \frac{e^{i 2 \pi f} -1 + e^{-i 2 \pi f} -1 }{i 2 \pi f}  $$

$$ X(f) = \frac{e^{i 2 \pi f} + e^{-i 2 \pi f} -2 }{i 2 \pi f}  $$

Utilizzo l'identità di Eulero $ e^{i \theta} + e^{-i \theta} = 2 \cos(\theta) $ per esprimere i termini esponenziali:

$$ X(f) = \frac{2 \cos(2 \pi f) - 2}{i 2 \pi f}  $$

$$ X(f) = \frac{ \cos(2 \pi f) - 1}{i \pi f}  $$

Ricordando l'identità trigonometriche $ \cos(2 \theta) - 1 = -2 \sin^2(\theta) $ ottengo:

$$ X(f) = \frac{-2 \sin^2(\pi f)}{i \pi f} $$

Moltiplico e divido per $ i $

$$ X(f) = \frac{-2 \sin^2(\pi f)}{i \pi f} \cdot \frac{i}{i} $$

$$ X(f) = \frac{-2 \sin^2(\pi f)}{i^2 \pi f} \cdot i $$

Sapendo che il quadrato dell'unità immaginaria è $ i^2=-1 $

$$ X(f) = \frac{-2 \sin^2(\pi f)}{(-1) \pi f} \cdot i $$

$$ X(f) = \frac{2 \sin^2(\pi f)}{\pi f} \cdot i $$

La trasformata diventa:

$$ X(f) = i \frac{2 \sin^2(\pi f)}{\pi f} $$

Questa è una funzione immaginaria pura.

A questo punto verifico la disparità

Noto che:

• \( \sin^2(\pi f) \) è una funzione pari rispetto a \( f \).
• \( \frac{1}{f} \) è una funzione dispari rispetto a \( f \).

Il prodotto di una funzione pari e una dispari è una funzione dispari.

Quindi, l'intera espressione $ \frac{\sin^2(\pi f)}{f} $ è una funzione dispari.

Pertanto, \( X(f) \) è una funzione immaginaria pura e dispari, come afferma il teorema.

La dimostrazione

Per ipotesi la funzione \( x(t) \) è una funzione reale e dispari nel dominio del tempo.

• Reale significa non ha la parte immaginaria
• Dispari significa che \( x(-t) = -x(t) \) ovvero  \( x(t) = -x(-t) \)

Essendo la funzione reale non ha parte immaginaria, quindi la funzione $ x(t) $ è uguale al suo coniugato complesso $ \overline{x(t)} $

$$ \overline{x(t)} = x(t) $$

La trasformata di Fourier di una funzione \( x(t) \) è definita come:

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} \, dt $$

Cambio la variabile di integrazione da \( t \) a \( t'=-t \). Questo implica che \( dt = -dt' \), quindi il differenziale si inverte.

Intoltre, quando t va da -∞ a +∞, la variabile t' va da +∞ a -∞. Quindi, l'integrale diventa:

$$ X(f) = \int_{\infty}^{-\infty} x(-t') e^{-i 2 \pi f (-t')} (-dt') $$

$$ X(f) = \int_{\infty}^{-\infty} x(-t') e^{i 2 \pi f t'} (-dt') $$

Riscrivo l'integrale con i limiti di integrazione corretti

$$ X(f) = \int_{-\infty}^{\infty} x(-t') e^{i 2 \pi f t'} \ dt' $$

Dato che \( x(-t) = -x(t) \) perché la funzione è dispari, posso sostituire \( x(-t') \) con \( -x(t') \)

$$ X(f) = \int_{-\infty}^{\infty} -x(t') e^{i 2 \pi f t'} \ dt' $$

$$ X(f) = - \int_{-\infty}^{\infty} x(t') e^{i 2 \pi f t'} \ dt' $$

Ora, voglio collegarla a \( X(-f) \) per dimostrare che \( X(f) \) è una funzione immaginaria pura.

Scrivo la trasformata di Fourier di \( x(t) \) a frequenza opposta, cioè \( -f \):

$$ X(-f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi (-f) t} \, dt  $$

$$ X(-f) =  \int_{-\infty}^{\infty} x(t) e^{i 2 \pi f t} \, dt. $$

Quindi, confrontando questa espressione con la relazione ottenuta prima $ X(f) = - \int_{-\infty}^{\infty} x(t') e^{i 2 \pi f t'} \, dt' $ noto che:

$$ X(-f) = - X(f) $$

Questa relazione mostra che \( X(f) \) è una funzione dispari rispetto a \( f \).

A questo punto, separo la parte reale e immaginaria di \( X(f) \)

Ricordo che la trasformata di Fourier può essere espressa in termini di parte reale e immaginaria come:

$$ X(f) = \int_{-\infty}^{\infty} x(t) \cos(2 \pi f t) \, dt - i \int_{-\infty}^{\infty} x(t) \sin(2 \pi f t) \, dt  $$

La riscrivo indicando le componenti X_R e X_I.

$$ X(f) = X_R(f) - i X_I(f) $$

Dove

$$ X_R(f) = \int_{-\infty}^{\infty} x(t) \cos(2 \pi f t) \, dt $$

$$ X_I(f) = \int_{-\infty}^{\infty} x(t) \sin(2 \pi f t) \, dt $$

A questo punto analizzo la parte reale e la parte immaginaria separatamente.

• Analisi della parte reale \( X_R(f) \):
  Poiché \( x(t) \) è una funzione dispari e \( \cos(2 \pi f t) \) è una funzione pari, il prodotto \( x(t) \cos(2 \pi f t) \) è una funzione dispari. L'integrale di una funzione dispari su un intervallo simmetrico è zero, quindi: $$
  X_R(f) = \int_{-\infty}^{\infty} x(t) \cos(2 \pi f t) \, dt = 0 $$
• Analisi della parte immaginaria \( X_I(f) \):
  Poiché \( x(t) \) è una funzione dispari e \( \sin(2 \pi f t) \) è anch'essa una funzione dispari, il prodotto \( x(t) \sin(2 \pi f t) \) è una funzione pari. L'integrale di una funzione pari su un intervallo simmetrico può essere diverso da zero: $$
  X_I(f) = \int_{-\infty}^{\infty} x(t) \sin(2 \pi f t) \, dt $$

In conclusione, poiché la parte reale \( X_R(f) = 0 \) è zero e la parte immaginaria \( X_I(f) \) è non nulla, la trasformata di Fourier \( X(f) \) è una funzione immaginaria pura.

$$ X(f) = X_R(f) - i X_I(f) $$

$$ X(f) = -i X_I(f) $$

Ho così dimostrato che se \( x(t) \) è una funzione reale e dispari, la sua trasformata di Fourier \( X(f) \) è una funzione immaginaria pura e dispari.

E così via.