Teorema di Fourier
Una funzione periodica può essere considerata come la somma di più sinusoidi. $$ f(t) = c_0 + \sum_{n=1}^{∞} c_k \cdot \sin(kωt+φ_k) $$ dove ω è la pulsazione dell'armonica fondamentale $$ ω = \frac{2π}{T}=2πf $$ La serie è detta serie di Fourier in forma polare.
La componente c0 è una costante che indica il valore medio (componente continua).
Le componenti successive c1...ck sono i coefficienti di Fourier e indicano l'ampiezza delle singole sinusoidi (armoniche).
$$ c_k = \frac{1}{T_0} \int_a^{a+T_0} f(t) \cdot e^{-jkωt} \: dt $$
La prima sinusoide (k=1) è detta armonica fondamentale, perché la sua frequenza f coincide con la funzione f(t).
$$ f = \frac{ω}{2π} $$
Dimostrazione. $$ f = \frac{ω}{2π} = \frac{2πf}{2π} =f $$
Le altre sinusoidi (k>1) sono armoniche secondarie, perché hanno un'ampiezza generalmente decrescente all'aumentare della frequenza e si presentano in frequenze multiple dell'armonica fondamentale.
Nota. Nel XIX secolo Fourier si accorse che una funzione periodica poteva essere decomposta in una somma infinita di seni e coseni (serie trigonometrica). La decomposizione in somma di armoniche è anche detto sviluppo in serie di Fourier e indica il passaggio dal dominio del tempo al dominio delle frequenze. Per un approfondimento vedere la serie di Fourier.
La serie di Fourier in forma cartesiana ed esponenziale
La serie di Fourier può essere rappresentata anche in forma cartesiana e esponenziale.
La serie di Fourier in forma cartesiana
$$ f(t) = c_0 + \sum_{k=1}^{∞} A_k \sin kωt + B_k \cos kωt $$
La serie di Fourier in forma esponenziale
$$ f(t) = \sum_{k=-∞}^{∞} E_k \cdot e^{jωt} $$
Il significato è lo stesso.
Nota. La pulsazione ω è il rapporto tra la circonferenza 2π e il periodo T della funzione. $$ ω = \frac{2π}{T} $$ Analogamente, essendo la frequenza f l'inverso del periodo T ossia f=1/T. $$ ω =2πf $$
Qual è la differenza tra rappresentazione polare, cartesiana e esponenziale?
La rappresentazione in forma esponenziale permette di costruire uno spettro bilatero perché considera anche le frequenze negative oltre a quelle positive.
Viceversa, la rappresentazione polare e cartesiana realizzano uno spettro unilatero con le sole frequenze positive.
Nota. Per passare dallo spettro bilatero a quello unilatero, basta considerare solo le frequenze positive con i valori raddoppiati.
Le condizioni di convergenza
Un segnale periodico approssimato tramite la serie di Fourier con un infinito numero di termini converge al segnale originale v(t) quando sono rispettate le seguenti condizioni di Dirichlet
- La funzione periodica v(t) ha un numero finito di minimi e di massimi per periodo
- La funzione periodica v(t) ha un numero finito di discontinuità per periodo
- La funzione periodica v(t) è integrabile e ha un'area finita per periodo
Queste condizioni sono sufficienti ma non necessarie per la convergenza della serie di Fourier.
L'effetto Gibbs
Nei punti di discontinuità la serie presenta un andamento detto fenomeno di Gibbs.
Esempio
Nel punto t0 la funzione reale v(t) ha un punto di discontinuità con un salto S.
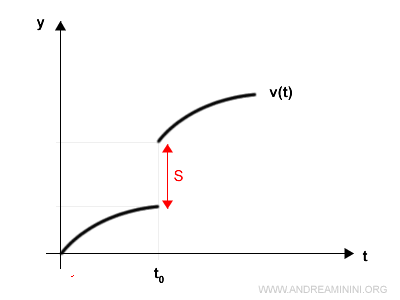
In questo punto la serie vN(t) converge al punto medio della discontinuità S/2.
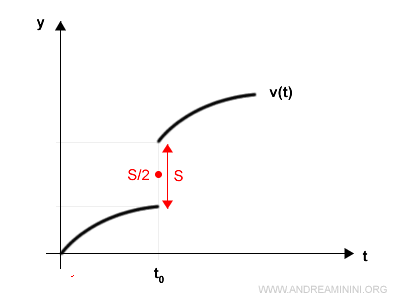
Si tratta di un'approssimazione del tutto ragionevole per studiare il segnale v(t) tramite Fourier.
Tuttavia, nei pressi del punto di discontinuità in t0 la serie presenta dei picchi anomali pari al 9% di S che anticipano e posticipano il salto.
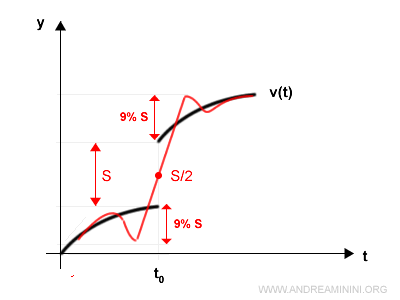
I picchi si presentano in un periodo di tempo pari a T0/2N prima e dopo.
$$ \lim_{N \rightarrow \infty} \frac{T_0}{2N} = 0,09 \cdot S $$
Come rappresentare le armoniche
Le armoniche mi permettono di rappresentare una funzione nel dominio della frequenza anziché del tempo.
Per rappresentare le armoniche traccio delle righe verticali su un diagramma cartesiano.
Sull'asse delle ordinate indico l'ampiezza, mentre sull'asse delle ascisse indico la frequenza.
Ogni riga è associata a un'armonica e ha un'altezza pari all'ampiezza dell'armonica assegnata.
Questa rappresentazione è detta spettro delle ampiezze del segnale.
A cosa serve lo spettro? Mi permette di analizzare la risposta a regime di un sistema con un segnale periodico in ingresso u(t) tramite la sovrapposizione delle risposte del sistema alle singole componenti sinusoidali del segnale in ingresso.
Oltre una certa frequenza il contributo delle armoniche diventa trascurabile. Pertanto, lo spettro è limitato alle armoniche più importanti.
La trasformata di Fourier
La trasformata di Fourier mi permette di scomporre un segnale in singole componenti nel dominio della frequenza, ognuna caratterizzata da un'ampiezza, una fase e una frequenza. $$ X(f) = \int_{-∞}^{+∞} x(t)e^{iωt} \: dt $$ dove $$ ω = \frac{2π}{T}=2πf $$
La somma delle singole componenti permette di ricostruire il segnale di partenza.
Per ricostruire il segnale nel dominio del tempo si utilizza l'antitrasformata di Fourier.
$$ x(t) = \int_{-∞}^{+∞} X(f) e^{iωt} df $$
Nota. La trasformata di Fourier prende il nome dal suo ideatore, il francese Jean Baptiste Joseph Fourier che le formulò nel 1822.
Qual è la differenza tra serie e trasformata di Fourier?
La trasformata di Fourier può essere applicata anche ai segnali non periodici.
La serie di Fourier, invece, è applicabile soltanto ai segnali periodici ( funzioni periodiche ).
Quindi, la trasformata consente di studiare molti più segnali nel dominio delle frequenze rispetto alla serie di Fourier.
E così via.
