Teorema della trasformata di Fourier per segnali reali e pari

Se un segnale \( x(t) \) è una funzione reale e pari, allora la sua trasformata di Fourier \( X(f) \) è una funzione reale pura e pari.

Questa è una proprietà fondamentale delle trasformate di Fourier applicata a segnali con simmetria rispetto all'origine (parità) e con valori reali.

Le condizioni da soddisfare sono le seguenti:

• Segnale reale: Un segnale \( x(t) \) è reale se \( x(t) = \overline{x(t)} \) , dove \( \overline{x(t)} \) indica il complesso coniugato di \( x(t) \).
• Segnale pari: Un segnale è pari se \( x(t) = x(-t) \).

Ora, considerando la trasformata di Fourier \( X(f) \) di \( x(t) \) nel dominio del tempo:

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt $$

Per un segnale pari, si può dimostrare che \( X(f) = X(-f) \), ovvero anche la trasformata di Fourier è pari.

$$ X(-f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt $$

Inoltre, dato che \( x(t) \) è reale, anche la sua trasformata di Fourier \( X(f) \) sarà una funzione reale pura, senza componente immaginaria.

Pertanto, la trasformata di Fourier di un segnale reale e pari è una funzione reale e pari. 

Spesso viene presentata come una delle proprietà simmetriche della trasformata di Fourier. Questa proprietà non è limitata a una particolare forma del segnale, ma si applica a qualsiasi segnale reale e pari. Quindi, non solo per i segnali rettangolari o di impulso gaussiano. Il segnale rettangolare è solo un esempio particolare di un segnale reale e pari. In sintesi, questa proprietà è generale per tutti i segnali che rispettano le condizioni di essere reali e pari.

Un esempio pratico

Faccio un esempio concreto con un segnale reale e pari, come un segnale rettangolare \( x(t) \) definito come:

$$
x(t) =
\begin{cases}
1 & \text{se} \ |t| \leq \frac{T}{2}, \\
0 & \text{se} \ |t| > \frac{T}{2}.
\end{cases} $$

Nel dominio del tempo questo segnale è reale perché non ha componenti immaginarie ed è pari (cioè \( x(t) = x(-t) \)).

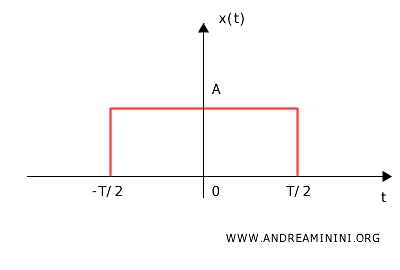
La trasformata di Fourier del segnale rettangolare \( x(t) \) è data da:

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt $$

Poiché \( x(t) = 0 \) per \( |t| > \frac{T}{2} \), l'integrale diventa:

$$ X(f) = \int_{-\frac{T}{2}}^{\frac{T}{2}} e^{-i 2 \pi f t} dt $$

Questo è un integrale standard di un segnale Rect che posso calcolare come:

$$ X(f) = \frac{\sin(\pi f T)}{\pi f} $$

Nota. Evito di scrivere di nuovo tutti i calcoli per giungere a questo risultato. Per vederli, rimando alla pagina degli appunti dove ho trattato in dettaglio la trasformata di Fourier di un segnale rettangolare.

Guardando il grafico della trasformata di Fourier X(f) nel dominio delle frequenze, mi accorgo immediatamente che la funzione è pari.

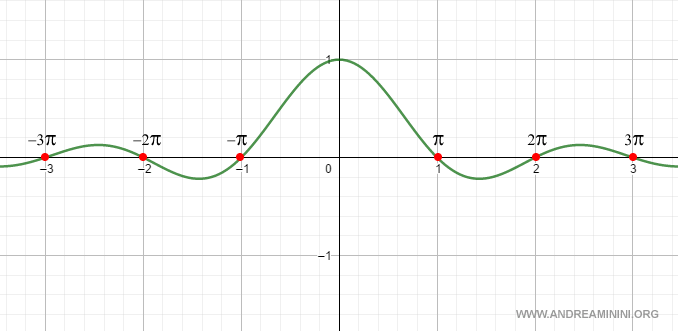
Pertanto, nel dominio delle frequenze la funzione ottenuta è \( X(f) = \frac{\sin(\pi f T)}{\pi f} \) che è:

• reale perché non ha una parte immaginaria
• pari perché \( X(f) = X(-f) \)

In conclusione, il segnale rettangolare \( x(t) \), che è reale e pari, ha una trasformata di Fourier \( X(f) \) che è anch'essa reale e pari.

La dimostrazione

Per ipotesi iniziale considero una funzione \( x(t) \) reale e pari.

Poiché la funzione è reale \( x(t) \), non ha la parte immaginaria, quindi \( x(t) \) è uguale al suo complesso coniugato \( \overline{x(t)} \)

$$ x(t) = \overline{x(t)} $$

La trasformata di Fourier \( X(f) \) di un segnale \( x(t) \) nel dominio del tempo è definita come:

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt $$

Per fare un confronto, calcolo anche la trasformata di Fourier di \( X(-f) \)

$$  X(-f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi (-f) t} dt $$

$$ X(-f)  = \int_{-\infty}^{\infty} x(t) e^{i 2 \pi f t} dt $$

A questo punto calcolo il complesso coniugato di \( X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt \).

$$ \overline{X(f)} = \int_{-\infty}^{\infty} x(t) e^{i 2 \pi f t} dt $$

Confrontando \( X(-f) \) con \( \overline{X(f)} \) si vede subito che sono uguali.

$$ X(-f) = \overline{X(f)} $$

Questo implica che \( X(f) \) non ha la parte immaginaria, ovvero è una funzione reale. 

Ora devo dimostrare che la trasformata $ X(f) $ è anche una funzione pari.

Per ipotesi iniziale la funzione \( x(t) \) è pari, quindi vale la proprietà \( x(t) = x(-t) \).

Considero la trasformata di Fourier \( X(f) \) di \( x(t) \)

$$ X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} dt $$

Ora, faccio il cambio di variabile \( t' = -t \).  Questo implica che \( dt = -dt' \), quindi il differenziale si inverte.

Quando t va da -∞ a +∞, allora t' va da +∞ a -∞. L'integrale diventa:

$$ X(f) = \int_{\infty}^{-\infty} x(-t') e^{-i 2 \pi f (-t')} (-dt') $$

$$ X(f) = \int_{\infty}^{-\infty} x(-t') e^{i 2 \pi f t'} (-dt') $$

Riscrivo l'integrale con i limiti di integrazione corretti

$$ X(f) = \int_{-\infty}^{\infty} x(-t') e^{i 2 \pi f t'} \ dt' $$

Dato che \( x(t) = x(-t) \), ovvero il segnale è pari, posso sostituire \( x(-t') \) con \( x(t') \)

$$ X(f) = \int_{-\infty}^{\infty} x(t') e^{i 2 \pi f t'} dt' $$

Quest'ultima è uguale a $ X(-f) = \int_{-\infty}^{\infty} x(t) e^{i 2 \pi f t} dt $

Ho così dimostrato che X(f)=X(-f)

$$ X(f) = X(-f) $$

Quindi, anche la trasformata di Fourier  \( X(f) \) è una funzione pari.

In conclusione, ho dimostrato che se il segnale \( x(t) \) è reale e pari, allora la funzione \( X(f) \) è una funzione reale e pari.

E così via.