La trasformata di Fourier del coseno

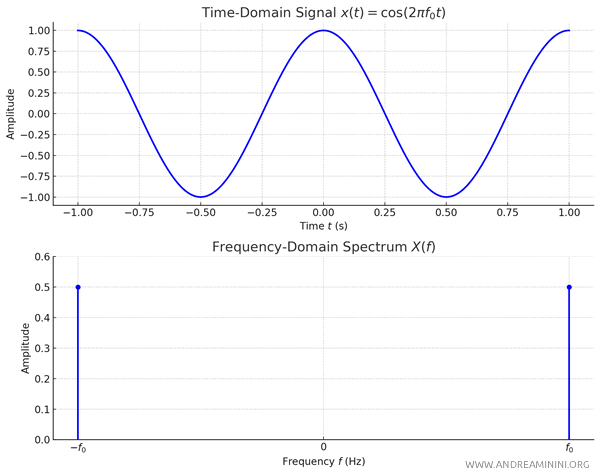
La trasformata di Fourier del coseno $$ x(t) = \cos(2 \pi f_0 t) $$ è composta da due Delta di Dirac centrate in \( f_0 \) e \( -f_0 \), con ampiezza pari a \( \frac{1}{2} \): $$ X(f) = \frac{1}{2} \left[ \delta(f - f_0) + \delta(f + f_0) \right] $$

Considerando anche l'effetto dell'ampiezza \( A \) e della fase \( \phi \).

$$ x(t) = A \cos(2\pi f_0 t + \phi) $$

la trasformata di Fourier è data da:

$$ X(f) = \frac{A}{2} \left[ e^{j\phi} \delta(f - f_0) + e^{-j\phi} \delta(f + f_0) \right]$$

Dove \( A \) è ampiezza, \( \phi \) è la fase, \( \delta \) è il Delta di Dirac centrato in \( +f_0 \) e \( -f_0 \).

Se \( A = 1 \) e \( \phi = 0 \) si ritorna al caso iniziale:  

$$ X(f) = \frac{1}{2} \left[ \delta(f - f_0) + \delta(f + f_0) \right] $$

Questa proprietà evidenzia come un segnale periodico (come il coseno) sia costituito nel dominio della frequenza da componenti discrete (spettri discreti), situate simmetricamente rispetto all'origine.

Nota. Lo spettro del coseno è simmetrico e reale, a differenza dello spettro del seno che è complesso e antisimmetrico con componenti puramente immaginarie.

La spiegazione

La trasformata di Fourier della funzione coseno nel dominio del tempo

$$ x(t) = \cos(2 \pi f_0 t) $$

posso trovarla calcolando l'integrale

$$ X(f) = \int_{-\infty}^{+\infty} x(t) \cdot e^{-j 2 \pi f t} dt $$

Tuttavia, è molto più semplice e rapido farlo sfruttando la rappresentazione della funzione coseno in termini di esponenziali complesse tramite la formula di Eulero.

$$ x(t) = \cos(2 \pi f_0 t) = \frac{e^{j 2 \pi f_0 t} + e^{-j 2 \pi f_0 t}}{2} $$

Pertanto, la funzione coseno in funzione del tempo \( x(t) = \cos(2 \pi f_0 t) \) posso scriverla come:

$$ x(t) = \frac{1}{2} e^{j 2 \pi f_0 t} + \frac{1}{2} e^{-j 2 \pi f_0 t} $$

A questo punto calcolo la trasformata di Fourier di ciascun termine.

$$ X(f) = F \left[ \frac{1}{2} e^{j 2 \pi f_0 t} + \frac{1}{2} e^{-j 2 \pi f_0 t} \right] $$

Per la proprietà della linearità la trasformata di Fourier di una somma è la somma delle trasformate.

$$ X(f) = F \left[ \frac{1}{2} e^{j 2 \pi f_0 t}  \right] + F \left[ \frac{1}{2} e^{-j 2 \pi f_0 t} \right] $$

$$ X(f) = \frac{1}{2}  \cdot F \left[ e^{j 2 \pi f_0 t}  \right] + \frac{1}{2}  \cdot F \left[ e^{-j 2 \pi f_0 t} \right] $$

In base alle trasformate note di Fourier che conosco so già che:

• La trasformata di \( e^{j 2 \pi f_0 t} \) è un impulso a \( f = f_0 \)
• La trasformata di \( e^{-j 2 \pi f_0 t} \) è un impulso a \( f = -f_0 \)

Di conseguenza, sostituendo questi termini ottengo la funzione nel dominio delle frequenze

$$ X(f) = \frac{1}{2} \delta(f - f_0) + \frac{1}{2} \delta(f + f_0) $$

Dove \( \delta(f) \) è la funzione delta di Dirac.

Quindi, la trasformata di Fourier di \( x(t) = \cos(2 \pi f_0 t) \) risulta:

$$ X(f) = \frac{1}{2} \delta(f - f_0) + \frac{1}{2} \delta(f + f_0) $$

Questo mostra che la trasformata di Fourier di un coseno puro si concentra in due impulsi in frequenza a \( \pm f_0 \). 

Questo metodo evita l'integrazione diretta e sfrutta proprietà note della trasformata di Fourier, rendendo il calcolo più semplice e rapido.

Nota. La funzione coseno nel tempo è una funzione reale e pari, la sua trasformata in frequenza è una funzione reale pura e pari, come prevede una delle principali proprietà della trasformata di Fourier.

Un esempio pratico

Considero il segnale nel tempo

$$ z(t) = \cos ( 2 \pi t ) $$

Senza fare altri calcoli so già che la sua trasformata di Fourier è

$$ Z(f) = \frac{1}{2} \left[ \delta(f - f_0) + \delta(f + f_0) \right] $$

Resta però da capire qual è il valore di $ f_0 $.

Per capirlo eguaglio l'argomento della funzione coseno $ 2 \pi t $ con il valore $ 2 \pi f_0  t $

$$ 2 \pi t = 2 \pi f_0 t $$

Ricavo $ f_0 $ e semplifico

$$ f_0 = \frac{2 \pi t}{2 \pi t} $$

$$ f_0 = 1 $$

Quindi, il valore da utilizzare nello spettro è $ f_0 = 1 $$

$$ Z(f) = \frac{1}{2} \left[ \delta(f - 1) + \delta(f + 1) \right] $$

 

E così via.