Serie di Fourier

Cos'è la serie di Fourier

La serie di Fourier è la rappresentazione di una funzione periodica tramite la combinazione lineare di funzioni sinusoidali (seno e coseno).
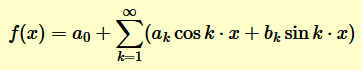
$f(x) = a_0 + \sum_{k=1}^{\infty} (a_k \cos k \cdot x + b_k \sin k \cdot x )$

I parametri a₀, a_k e b_k sono detti coefficienti di Fourier.

I coefficienti di Fourier dipendono dai valori della funzione f(x) nell'intervallo 2p.

A cosa serve?

Con un'opportuna configurazione dei parametri, la serie rappresenta le funzioni che hanno la caratteristica di essere oscillanti e periodiche.

E' usata in fisica, in telecomunicazioni e in elettronica.

Nota. La serie venne ideata da Jospeh Furier agli inizi del XIX secolo per studiare le oscillazioni di mezzi elastici. E' ancora oggi alla base dello studio dei segnali e di molti fenomeni fisici ( es. vibrazioni di una corda o di una superficie elastica ).

Come costruire la curva di Fourier
Le funzioni sviluppabili in serie di Fourier
Un esempio pratico

Come costruire la curva di Fourier

Per semplicità tralascio i parametri a₀,a_k,b_k e li considero costanti pari a

$$ a_0 = 0 \\ a_k = 1 \\ b_k=1 $$

La più semplice serie di Fourier di ordine k=1 ( detta fondamentale ) è la seguente:

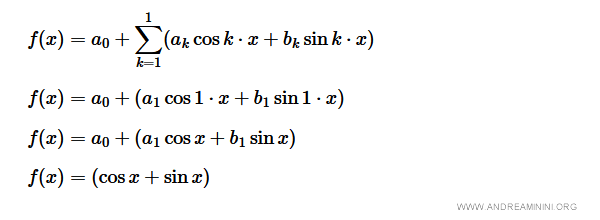
$f(x) = a_0 + \sum_{k=1}^{1} (a_k \cos k \cdot x + b_k \sin k \cdot x ) $$ $$ f(x) = a_0 + (a_1 \cos 1 \cdot x + b_1 \sin 1 \cdot x ) $$ $$ f(x) = a_0 + (a_1 \cos x + b_1 \sin x ) $$ $$ f(x) = (\cos x + \sin x )$

Questa funzione approssima un'onda quadra di periodo T=2π

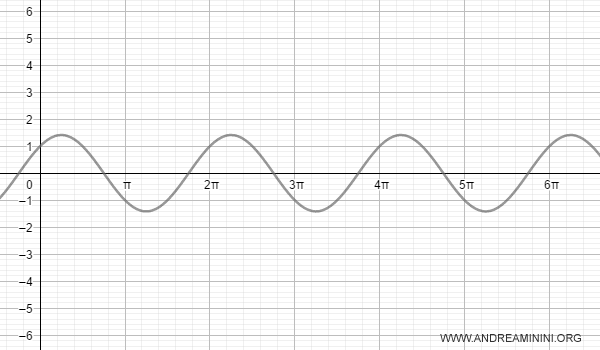
la serie di Fourier di ordine 1

La serie di Fourier di ordine k=2 è la seguente:

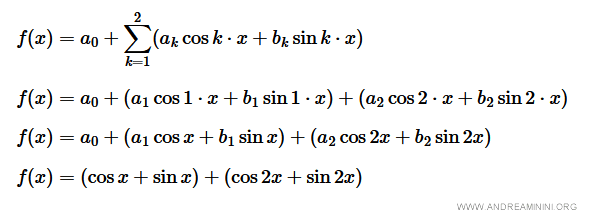
$f(x) = a_0 + \sum_{k=1}^{2} (a_k \cos k \cdot x + b_k \sin k \cdot x ) $$ $$ f(x) = a_0 + (a_1 \cos 1 \cdot x + b_1 \sin 1 \cdot x ) + (a_2 \cos 2 \cdot x + b_2 \sin 2 \cdot x ) $$ $$ f(x) = a_0 + (a_1 \cos x + b_1 \sin x ) + (a_2 \cos 2x + b_2 \sin 2x ) $$ $$ f(x) = (\cos x + \sin x ) + (\cos 2x + \sin 2x )$

La funzione assume un aspetto differente

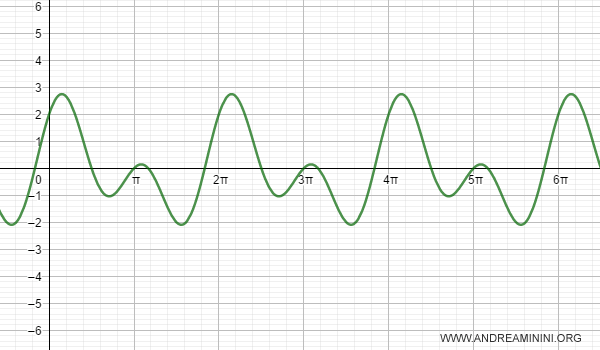
un esempio di serie di Fourier di ordine 2

La serie di Fourier di ordine k=3 è la seguente:

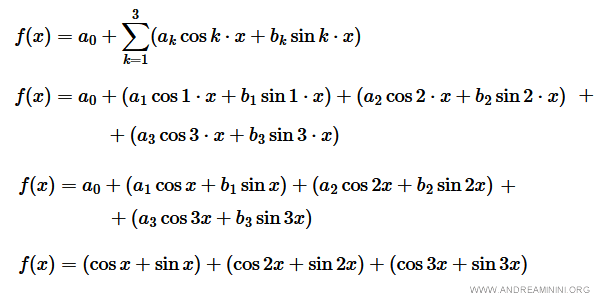
$f(x) = a_0 + \sum_{k=1}^{3} (a_k \cos k \cdot x + b_k \sin k \cdot x ) $$ $$ f(x) = a_0 + (a_1 \cos 1 \cdot x + b_1 \sin 1 \cdot x ) + (a_2 \cos 2 \cdot x + b_2 \sin 2 \cdot x ) + (a_3 \cos 3 \cdot x + b_3 \sin 3 \cdot x ) $$ $$ f(x) = a_0 + (a_1 \cos x + b_1 \sin x ) + (a_2 \cos 2x + b_2 \sin 2x ) + (a_3 \cos 3x + b_3 \sin 3x ) $$ $$ f(x) = (\cos x + \sin x ) + (\cos 2x + \sin 2x ) + (\cos 3x + \sin 3x )$

L'aspetto del grafico muta ancora

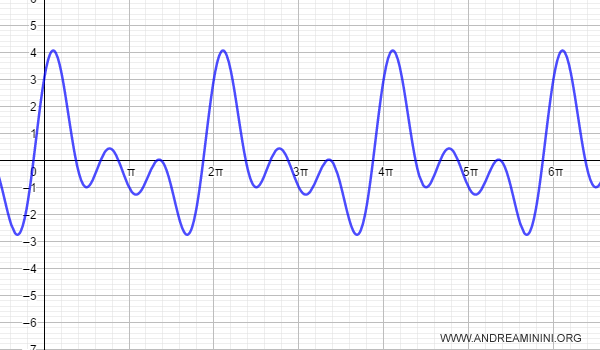
l'aspetto della curva

Con gli opportuni parametri a₀, a_k, b_k, k ( detti coefficienti di Fourier) posso ricostruire il grafico qualsiasi funzione periodica oscillante sinusoidale.

Nel prossimo paragrafo spiego come si calcolano i coefficienti di Fourier.

Nota. Più in basso in questa pagina ho scritto un esempio pratico di calcolo (passo dopo passo) della serie di Fourier.

Le funzioni sviluppabili in serie di Fourier

Una funzione f(x) periodica di periodo 2π e definita nell'insieme dei numeri reali è sviluppabile in serie di Fourier se esistono i valori a₀, a_k e b_k con k∈N tali che
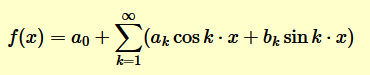
$f(x) = a_0 + \sum_{k=1}^{\infty} (a_k \cos k \cdot x + b_k \sin k \cdot x )$

I coefficienti di Fourier a₀, a_k e b_kdipendono dai valori della funzione f(x) nell'intervallo di lunghezza 2π.

Come determinare i coefficienti di Fourier

Nell'intervallo [-π,π] i coefficienti di Fourier sono determinati dalle seguenti formule:

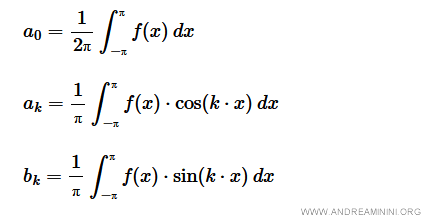
$a_0 = \frac{1}{2π} \int_{-π}^π f(x) \: dx $$ $$ a_k = \frac{1}{π} \int_{-π}^π f(x) \cdot\cos (k \cdot x) \: dx $$ $$ b_k = \frac{1}{π} \int_{-π}^π f(x) \cdot\sin (k \cdot x) \: dx$

Per ogni k=1,....,n.

Nota. La serie di Fourier converge alla f(x) nei punti in cui la funzione è continua. Nei punti in cui è discontinua, invece, la serie converge al valore medio del limite destro e del limite sinistro in ogni punto di discontinuità.

Un esempio pratico

Provo a ricostruire un segnale a impulsi.

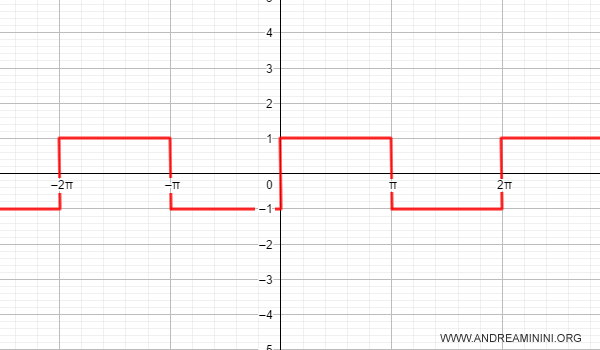
un esempio di funzione

Si tratta di una funzione periodica di lunghezza 2π che assume i seguenti valori nell'intervallo [-π,π].

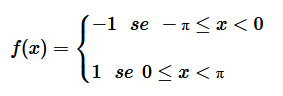
$f(x) = \begin{cases} -1 \:\:\:se\:\: -π \le x<0 \\ \\ 1 \:\:\:se\:\: 0 \le x<π \end{cases}$

Per prima cosa calcolo il parametro a₀

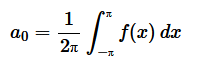
$a_0 = \frac{1}{2π} \int_{-π}^π f(x) \: dx$

Applico la proprietà additiva dell'integrale per separare i due intervalli (-π,0) e (0,π)

$$ a_0 = \frac{1}{2 \pi} \cdot [ \int_{- \pi}^0 f(x) \ dx + \int_0^{\pi} f(x) \ dx ] $$

Nell'intervallo (-π,0) la f(x) = -1 mentre nell'intervallo (0,π) la f(x)=1

$$ a_0 = \frac{1}{2 \pi} \cdot [ \int_{- \pi}^0 -1 \ dx + \int_0^{\pi} 1 \ dx ] $$

$$ a_0 = \frac{1}{2 \pi} \cdot [ -1 \cdot \int_{- \pi}^0 \ dx + 1 \cdot \int_0^{\pi} 1 \ dx ] $$

$$ a_0 = \frac{1}{2 \pi} \cdot [ -1 \cdot (0 - (- \pi) ) + 1 \cdot ( \pi - 0 ) ] $$

$$ a_0 = \frac{1}{2 \pi} \cdot [ - \pi + \pi ] $$

$$ a_0 = \frac{1}{2 \pi} \cdot 0 $$

$$ a_0 = 0 $$

Quindi, il parametro a₀ è uguale a zero.

Poi calcolo il parametro a_k

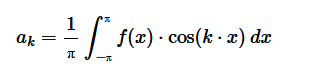
$a_k = \frac{1}{π} \int_{-π}^π f(x) \cdot\cos (k \cdot x) \: dx$

Separo gli intervalli (-π,0) e (0,π) dell'integrale

$a_k = \frac{1}{π} \cdot [ \int_{-π}^0 f(x) \cdot \cos (k \cdot x) \: dx + \int_{0}^π f(x) \cdot \cos (k \cdot x) \: dx ]$

Nell'intervallo (-π,0) la f(x) = -1 mentre nell'intervallo (0,π) la f(x)=1

$a_k = \frac{1}{π} \cdot [ \int_{-π}^0 (-1) \cdot \cos (k \cdot x) \: dx + \int_{0}^π 1 \cdot \cos (k \cdot x) \: dx ] $$ $$ a_k = \frac{1}{π} \cdot [ -1 \cdot \int_{-π}^0 \cos (k \cdot x) \: dx + 1 \cdot \int_{0}^π \cos (k \cdot x) \: dx ] $$ Nota. La primitiva di cos(kx) è $$ \int \cos (kx) \:dx = \sin(kx)$

Applico il teorema fondamentale dell'integrazione

$$ a_k = \frac{1}{π} \cdot \begin{bmatrix} -1 \cdot [ \frac{1}{k} \sin (k \cdot x) ]_{-π}^0 + 1 \cdot [ \frac{1}{k} \sin (k \cdot x) ]_{0}^π \end{bmatrix} $$ $$ a_k = \frac{1}{π} \cdot \begin{bmatrix} -1 \cdot [ \frac{1}{k} \sin (k \cdot 0) - \frac{1}{k} \sin (k \cdot (-π)) ] + 1 \cdot [ \frac{1}{k} \sin (k \cdot π) - \frac{1}{k} \sin (k \cdot 0) ] \end{bmatrix} $$ $$ a_k = \frac{1}{π} \cdot \begin{bmatrix} - \frac{1}{k} \sin (k \cdot 0) + \frac{1}{k} \sin (k \cdot (-π)) + \frac{1}{k} \sin (k \cdot π) - \frac{1}{k} \sin (k \cdot 0) \end{bmatrix} $$ $$ a_k = \frac{1}{π} \cdot \begin{bmatrix} - \frac{2}{k} \sin (k \cdot 0) + \frac{1}{k} \sin (k \cdot (-π)) + \frac{1}{k} \sin (k \cdot π) \end{bmatrix} $$

Poiché il seno di zero è zero per qualsiasi k, il primo termine si annulla sin(k·0)=0

$$ a_k = \frac{1}{π} \cdot \begin{bmatrix} \frac{1}{k} \sin (k \cdot (-π)) + \frac{1}{k} \sin (k \cdot π) \end{bmatrix} $$

Il seno è una funzione dispari, quindi sin(-π) = - sin(π)

$$ a_k = \frac{1}{π} \cdot \begin{bmatrix} - \frac{1}{k} \sin (k \cdot (π)) + \frac{1}{k} \sin (k \cdot π) \end{bmatrix} $$ $$ a_k = \frac{1}{π} \cdot \begin{bmatrix} 0 \end{bmatrix} $$ $$ a_k = 0 $$

Quindi, per qualsiasi k il parametro a_k=0.

Infine calcolo il parametro b_k

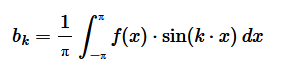
$b_k = \frac{1}{π} \int_{-π}^π f(x) \cdot\sin (k \cdot x) \: dx$

Separo gli intervalli (-π,0) e (0,π) dell'integrale

$b_k = \frac{1}{π} \cdot [ \int_{-π}^0 f(x) \cdot\sin (k \cdot x) \: dx + \int_{0}^π f(x) \cdot\sin (k \cdot x) \: dx ]$

Nell'intervallo (-π,0) la f(x) = -1 mentre nell'intervallo (0,π) la f(x)=1

$b_k = \frac{1}{π} \cdot [ \int_{-π}^0 (-1) \cdot\sin (k \cdot x) \: dx + \int_{0}^π 1 \cdot \sin (k \cdot x) \: dx ] $$ $$ b_k = \frac{1}{π} \cdot [ -1 \cdot \int_{-π}^0 \sin (k \cdot x) \: dx + 1 \cdot \int_{0}^π \sin (k \cdot x) \: dx ] $$ Nota. La primitiva di sin kx è $$ \int \sin (k \cdot x) = - \frac{1}{k} \cdot \cos (k \cdot x)$

Applico il teorema fondamentale dell'integrazione

$b_k = \frac{1}{π} \cdot \begin{bmatrix} -1 \cdot [ - \frac{\cos (k \cdot x)}{k} ]_{-π}^0 + 1 \cdot [ - \frac{\cos (k \cdot x)}{k} ]_{0}^π \end{bmatrix} $$ $$ b_k = \frac{1}{π} \cdot \begin{bmatrix} [ \frac{\cos (k \cdot x)}{k} ]_{-π}^0 -[ \frac{\cos (k \cdot x)}{k} ]_{0}^π \end{bmatrix} $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} [ \cos (k \cdot x) ]_{-π}^0 - [ \cos (k \cdot x) ]_{0}^π \end{bmatrix} $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} [ \cos (k \cdot 0) - \cos (k \cdot (-π)) ] - [ \cos (k \cdot π) - \cos (k \cdot 0) ] \end{bmatrix} $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} \cos (k \cdot 0) - \cos (k \cdot (-π)) - \cos (k \cdot π) + \cos (k \cdot 0) \end{bmatrix} $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} 2 \cos (k \cdot 0) - \cos (k \cdot (-π)) - \cos (k \cdot π) \end{bmatrix} $$ Nota. Il coseno è una funzione pari $$ f(-x)=f(x) $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} 2 \cos (k \cdot 0) - \cos (k \cdot π) - \cos (k \cdot π) \end{bmatrix} $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} 2 \cos (k \cdot 0) - 2 \cos (k \cdot π) \end{bmatrix} $$ Sapendo che cos(0)=1 per qualsiasi valore di k $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} 2 \cos (k \cdot 0) - 2 \cos (k \cdot π) \end{bmatrix} $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} 2 \cdot 1 - 2 \cos (k \cdot π) \end{bmatrix} $$ $$ b_k = \frac{1}{kπ} \cdot \begin{bmatrix} 2 - 2 \cos (k \cdot π) \end{bmatrix} $$ $$ b_k = \frac{2}{kπ} \cdot \begin{bmatrix} 1 - \cos (k \cdot π) \end{bmatrix}$

Il valore di bk cambia a seconda se k è pari o dispari.

Se k è dispari, si ha cos(π) = -1 perché cos(180°)=-1
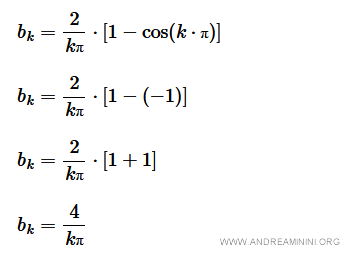
$b_k = \frac{2}{kπ} \cdot \begin{bmatrix} 1 - \cos (k \cdot π) \end{bmatrix} $$ $$ b_k = \frac{2}{kπ} \cdot \begin{bmatrix} 1 - (-1) \end{bmatrix} $$ $$ b_k = \frac{2}{kπ} \cdot \begin{bmatrix} 1 +1 \end{bmatrix} $$ $$ b_k = \frac{4}{kπ}$
Se k è pari, si ha cos(2π) = 1 perché cos(360°)=cos(0°)=1
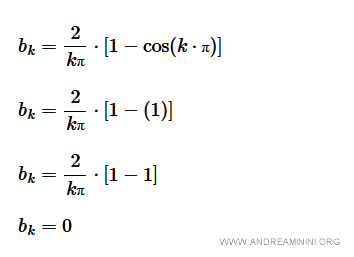
$$$ b_k = \frac{2}{kπ} \cdot \begin{bmatrix} 1 - \cos (k \cdot π) \end{bmatrix} $$ $$ b_k = \frac{2}{kπ} \cdot \begin{bmatrix} 1 - (1) \end{bmatrix} $$ $$ b_k = \frac{2}{kπ} \cdot \begin{bmatrix} 1 - 1 \end{bmatrix} $$ $$ b_k = 0 $$.$

Nota. Ricapitolando, i coefficienti di Fourier sono
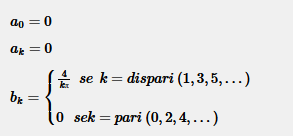
$a_0 = 0 $$ $$ a_k = 0 $$ $$ b_k = \begin{cases} \frac{4}{kπ} \:\: se \:\: k=dispari \: (1,3,5,...) \\ \\ 0 \:\:\: se k=pari \: (0,2,4,...) \end{cases}$

Posso cominciare a scrivere la serie di Fourier.

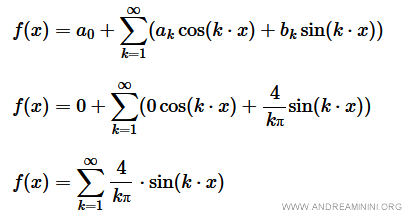
$f(x) = a_0 + \sum_{k=1}^{\infty} (a_k \cos (k \cdot x) + b_k \sin (k \cdot x) ) $$ $$ f(x) = 0 + \sum_{k=1}^{\infty} (0 \cos (k \cdot x) + \frac{4}{kπ} \sin (k \cdot x) ) $$ $$ f(x) = \sum_{k=1}^{\infty} \frac{4}{kπ} \cdot \sin (k \cdot x)$

Devo considerare soltanto k dispari ossia k=1, 3, 5, ... perché per k pari il termine è nullo

Per k=1

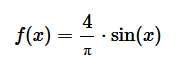
$f(x) = \frac{4}{π} \cdot \sin (x)$

Nel grafico la serie di Fourier è di colore blu e approssima la funzione f(x) di colore rosso in modo molto semplice.

E' detta serie di Fourier fondamentale.

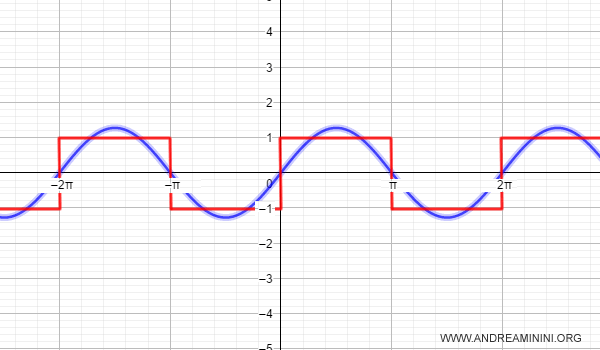
la serie fondamentale di Fourier

Per k=3

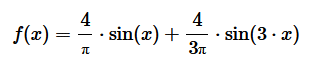
$f(x) = \frac{4}{π} \cdot \sin (x) + \frac{4}{3π} \cdot \sin (3 \cdot x)$

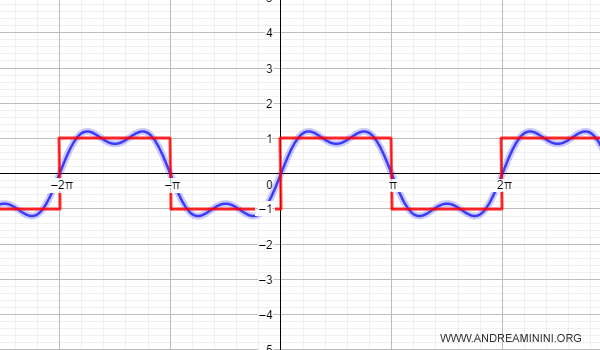
La serie di Fourier di ordine k=3 approssima meglio la funzione f(x).

Comincia a prendere la forma dell'impulso.

la serie di Fourier di ordine k=3

Per k=5

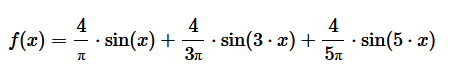
$f(x) = \frac{4}{π} \cdot \sin (x) + \frac{4}{3π} \cdot \sin (3 \cdot x) + \frac{4}{5π} \cdot \sin (5 \cdot x)$

La serie di Fourier di ordine k=5 è ancora più precisa nell'approssimare la funzione.

E' meglio della precedente.

la serie di Fourier con k=5

Il risultato è già soddisfacente. La serie di Fourier stima la funzione abbastanza bene.

Potrei comunque migliorare ulteriormente l'approssimazione usando valori k ancora più alti ( es. k=7, 9, 11, 13, ... ).

Con questo esempio ho spiegato la serie di Fourier a mio figlio. Spero sia utile anche ad altri.

E così via