Teoria delle categorie

La teoria delle categorie è un ambito matematico che si occupa di strutture astratte e delle loro interazioni. In particolare, una categoria è composta da "oggetti" e "morfismi" (chiamati anche freccie) che collegano questi oggetti.

Dove un morfismo in questo contesto è un'astrazione di funzioni tra strutture matematiche.

Le categorie posso considerarle come un terzo livello di astrazione dopo gli elementi di un insieme e le strutture definite sugli insiemi (es. gruppi, anelli, campi, spazi vettoriali, ecc.).

A cosa serve?

La teoria delle categorie è utile per unificare diversi concetti matematici e per fornire una struttura ad alta astrazione che può essere applicata in vari rami della matematica, della fisica, dell'informatica e oltre.

In altre parole permette di trasferire intuizioni e risultati da una struttura ad un'altra, ovvero da un campo del sapere a un altro, evidenziando le proprietà strutturali universali al di là dei dettagli specifici delle strutture coinvolte. 

Un'idea nata in un contesto possa essere trasferita e adattata per risolvere problemi in ambiti completamente diversi.

Esempio. L'algoritmo di Dijkstra è stato originariamente sviluppato per la ricerca del percorso minimo in una rete informatica di computer. Visto più in astratto, questo algoritmo trova il percorso più breve tra un nodo di partenza e tutti gli altri nodi in un grafo ponderato.

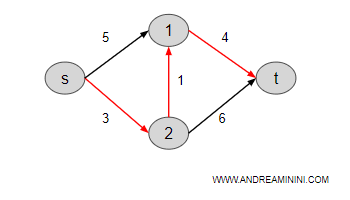
Oggi l'utilità di questo algoritmo si estende ben oltre l'informatica. Nella logistica è utilizzato per ottimizzare i percorsi di consegna, minimizzando il tempo o la distanza percorsa dai veicoli. Inoltre, aiuta a progettare sistemi di trasporto pubblico efficienti, individuando i percorsi più rapidi attraverso una città. Nella biologia computazionale è impiegato per analizzare le reti di interazione tra proteine, identificando i percorsi di segnalazione più importanti. Nell'analisi di reti economiche o finanziarie determina le vie più efficienti per il flusso di capitali o informazioni, ecc. In tutti questi campi, l'essenza dell'algoritmo di Dijkstra si rivela cruciale. Un'idea nata in ambito informatico ha trovato applicazioni in ambiti molto diversi da quello di origine.

Lo scopo della teoria delle categorie è individuare la struttura astratta dietro a diversi ambiti matematici e scientifici, permettendo così di esplorare e comprendere le relazioni e le interazioni tra oggetti e morfismi in maniera universale, indipendentemente dai dettagli specifici delle singole discipline.

Questo consente di trasferire metodi e risultati tra campi diversi, rivelando proprietà comuni e fornendo nuove intuizioni attraverso un linguaggio comune e formalizzato.

Le componenti della teoria delle categorie

Le componenti essenziali della teoria delle categorie sono le seguenti:

• Categorie
  Una categoria è un universo di "oggetti" collegati da "morfismi", che fungono da ponti tra questi oggetti rispettando regole di composizione ben definite.

  Esempio. Un esempio classico di categoria è la categoria degli insiemi, chiamata Set. In questa categoria, gli oggetti sono tutti i possibili insiemi. I morfismi sono tutte le funzioni possibili tra gli insiemi (oggetti), con la composizione di morfismi che corrisponde alla usuale composizione di funzioni (es. funzione composta).

• Oggetti
  Gli oggetti possono essere qualsiasi cosa, da insiemi a spazi, a strutture più complesse come anelli o spazi vettoriali. Gli oggetti sono i nodi fondamentali nei quali i morfismi "atterrano" o "partono".

  Esempio. I gruppi sono gli oggetti della categoria dei Gruppi, nota comunemente come Grp. In questa categoria, gli oggetti sono tutti i gruppi, e i morfismi sono le funzioni omomorfismi tra gruppi, che preservano l'operazione di gruppo. La composizione di questi morfismi è data dalla composizione usuale di funzioni, garantendo che le proprietà strutturali dei gruppi vengano mantenute.

• Morfismi
  I morfismi rappresentano le relazioni o le funzioni tra oggetti. Ogni morfismo ha un oggetto di partenza e un oggetto di arrivo. Nella teoria delle categorie, le composizioni di morfismi seguono regole precise: devono essere associative e deve esistere un morfismo identità per ogni oggetto, che agisce come un elemento neutro nella composizione.

  Esempio. Un esempio di morfismo è un omomorfismo di gruppi, come la funzione \( f: \mathbb{Z} \rightarrow \mathbb{Z}_6 \) definita da \( f(x) = x \mod 6 \). Questo morfismo rispetta l'operazione di addizione degli interi, assicurando che la somma di due elementi nel dominio venga mappata nella somma dei loro corrispondenti nel codominio modulo 6 nell'aritmetica modulare.

• Composizione di morfismi
  La composizione dei morfismi è una delle operazioni fondamentali in teoria delle categorie. Se \( f \) è un morfismo da \( A \) a \( B \), e \( g \) è un morfismo da \( B \) a \( C \), allora esiste un morfismo composto \( g \circ f \) da \( A \) a \( C \).

  Esempio. Considero due funzioni: \( f: \mathbb{R} \to \mathbb{R} \) definita da \( f(x) = x+1 \) e \( g: \mathbb{R} \to \mathbb{R} \) definita da \( g(x) = 2x \). La composizione di questi morfismi, denotata come \( g \circ f \), è una nuova funzione da \( \mathbb{R} \) a \( \mathbb{R} \) che si calcola applicando prima \( f \) e poi \( g \). Il risultato finale è la funzione composta g[f(x)]. $$ g[f(x)] = 2(x+1) = 2x + 2 $$

• Identità
  Ogni oggetto in una categoria ha un morfismo identità, che serve come un elemento neutro per la composizione. Questo significa che la composizione di qualsiasi morfismo con l'identità restituisce il morfismo originale.

  Esempio. Considero l'insieme dei numeri reali \( \mathbb{R} \) come oggetto in una categoria. L'identità di questo oggetto è la funzione \( \text{id}_{\mathbb{R}}: \mathbb{R} \to \mathbb{R} \) definita da \( \text{id}_{\mathbb{R}}(x) = x \), che lascia ogni elemento del dominio invariato. Questa funzione agisce come l'elemento neutro nella composizione di funzioni, mantenendo inalterato ogni morfismo che viene composto con essa.

in matematica è utile studiare le relazioni tra diverse strutture attraverso le funzioni che le collegano, ovvero i morfismi.

Questo approccio permette di concentrarsi sulle proprietà e le relazioni generali piuttosto che sui singoli elementi (oggetti) delle strutture, perché offre una visione più unificata e flessibile della matematica.

In questo modo le strutture matematiche sono definite in base a come si trasformano una nell'altra, piuttosto che delle loro caratteristiche isolate.

La storia della teoria delle categorie

La teoria delle categorie venne introdotta per la prima volta negli anni '40 del XX secolo dai matematici Samuel Eilenberg e Saunders Mac Lane.

Il loro scopo originario era quello di formalizzare e studiare strutture complesse in topologia algebrica, in particolare per quanto riguarda i concetti di trasformazione naturale e funtori, che erano essenziali per comprendere le relazioni tra vari tipi di coomologia.

Nel corso degli anni, la teoria delle categorie si è estesa ben oltre la topologia, influenzando profondamente diverse aree della matematica pura e applicata.

La sua capacità di rivelare connessioni strutturali profonde tra diversi campi matematici ha portato a nuove intuizioni e metodi in algebra, logica, teoria degli insiemi, informatica teorica e persino in fisica teorica.

Negli anni '60 e '70, la teoria delle categorie ha consolidato ulteriormente la sua importanza con lo sviluppo di concetti come categorie monoidali, categorie superiori e topos, che hanno arricchito la teoria fornendo nuovi strumenti e prospettive.

Oggi, rimane un'area di studio in continua evoluzione, dimostrando la sua versatilità come linguaggio matematico universale.

 E così via.