Gli oggetti nelle categorie

Nella teoria delle categorie, gli oggetti sono entità astratte che variano a seconda della categoria. Possono essere insiemi, gruppi, ecc.

Gli oggetti, insieme ai morfismi, sono gli elementi fondamentali che costituiscono una categoria.

Essendo entità astratte, gli oggetti possono rappresentare un'ampia gamma di concetti matematici.

Nota. I morfismi, invece, definiscono le relazioni tra gli oggetti e sono rappresentati come frecce.

Nella teoria delle categorie non è importante sapere con precisione qual è la natura degli oggetti, quello che veramente conta sono le relazioni tra gli oggetti ossia i morfismi.

Graficamente gli oggetti sono rappresentati come i nodi di un grafo orientato (digrafo) mentre i morfismi sono gli archi che collegano i nodi.

Esempio

Nella categoria "Set" gli oggetti sono gli insiemi.

Ad esempio, per ipotesi definisco una categoria composta solo da due insiemi A e B

$$ A = \{ 1,2,3 \} $$

$$ B = \{ a,b,c \} $$

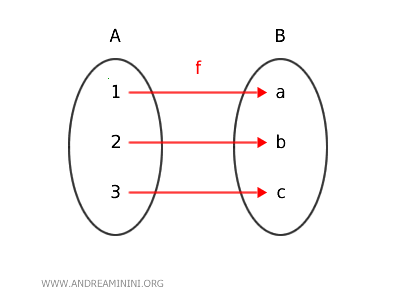
Un morfismo $ f: A \rightarrow b $ potrebbe essere una funzione che collega gli elementi dell'insieme A con quelli dell'insieme B.

$$ f(1) = a $$

$$ f(2) = b $$

$$ f(3) = c $$

In altre parole, mentre gli oggetti nelle categorie sono rappresentazioni di entità matematiche di varia natura, i morfismi sono gli strumenti attraverso i quali queste entità vengono collegate e analizzate.

E così via