Aritmetica modulare
Cos'è l'aritmetica modulare
L'aritmetica modulare è una disciplina matematica che studia le applicazioni dei numeri interi entro un determinato modulo.
E' detta anche aritmetica dell'orologio perché i numeri interi si avvolgono su stessi quando raggiungono il modulo (o un multiplo del modulo).
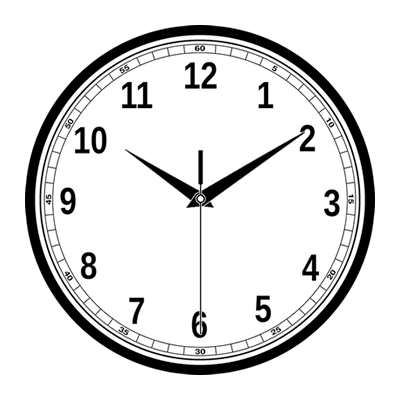
Così come accade alle lancette dell'orologio, quando raggiungono le 12 ripartono da 0, anche i numeri interi nell'aritmetica modulare ripartono da capo.
Chi l'ha ideata? L'aritmetica modulare venne ideata da Carl Friedrich Gauss nel 1801 nel trattato Disquisitiones Arithmeticae.
Un esempio pratico
Ho un insieme S composto da 10 numeri interi { 0,1,2,3,4,5,6,7,8,9 }
Nell'aritmetica tradizionale l'addizione 5+5 è uguale a 10.
$$ 5+5 = 10 $$
Nell'aritmetica modulare, invece, il numero 10 non è incluso nell'insieme S.
In questo caso il risultato è 0 perché il computo riparte da capo una volta oltrepassato il modulo.
$$ 5+5=0 $$
Questo accade perché l'insieme dei numeri S non è infinito, bensì S un insieme finito composto da 10 numeri.
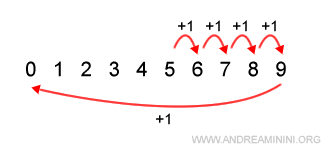
In questo caso il modulo è uguale a 10.
$$ \mod 10 $$
Nota. Potrei comunque creare aritmetiche modulari con modulo 8, 6, ecc. Il principio è sempre lo stesso.
C'è un'equivalenza tra il risultato dell'aritmetica decimale e quello dell'aritmetica su modulo 10.
$$ 10 \equiv 0 \mod 10 $$
Con lo stesso criterio nell'aritmetica modulare posso svolgere le altre somme.
$$ 5+6=1 \\ 5+7=2 \\ 5+8=3 $$
Nota. Lo stesso vale per qualsiasi multiplo del modulo e per qualsiasi altra operazione aritmetica ( somma, sottrazione, ecc. ).
Per semplificare la spiegazione costruisco la tavola di composizione della somma modulare.
| a+b | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 |
| 7 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 8 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 9 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Con lo stesso metodo posso costruire la tavola della sottrazione modulo 10 o di altri moduli e operazioni.
Le congruenze
Due numeri si dicono congruenti tra loro se divisi per m hanno lo stesso resto.
Esempio
I numeri 20 e 5 sono congruenti con il modulo 3
$$ 20 \equiv 5 \mod 3 \Rightarrow \begin{cases} \frac{20}{3} = 6 \mod 2 \\ \frac{5}{3} = 1 \mod 2 \end{cases} $$
perché entrambi i numeri divisi per 3 hanno lo stesso resto 2.
$ 20:3 = 6 $ con resto $ r=2 $
$ 5:3 = 1 $ con resto $ r=2 $
E così via.
