Le categorie
Una categoria è una collezione di oggetti e di morfismi.
Dove un oggetto può essere qualsiasi cosa, ad esempio un insieme, un gruppo, un vettore, ecc.
I morfismi, invece, sono le relazioni tra gli oggetti. Spesso sono indicati come una freccia che parte da un oggetto detto "dominio" e arriva a un altro oggetto detto "codominio". In altre parole, i morfismi sono delle funzioni tra gli oggetti.
Ad esempio, indico con "Set" una categoria composta da due insiemi A e B $$ Obj(Set) = \{A, B \} $$ I due insiemi A e B sono gli oggetti della categoria. $$ A = \{ 2, 3, 5 \} $$ $$ B = \{ 4, 9, 25 \} $$ Un morfismo potrebbe essere la funzione f(x) = x2 che va da A a B $$ f: A \rightarrow B $$ In genere l'insieme di tutti i morfismi in una categoria viene indicato con il simbolo $ Mor(Set) $.
Appartengono alla categoria anche le composizioni di morfismi e i morfismi identità.
- La composizione di morfismi
Quando il codominio di una funzione f: è uguale al dominio di un altra funzione g, posso comporre le due funzioni. Il risultato è una funzione composta $ f \circ g $ - Il morfismo identità
In una categoria ogni oggetto è associato a un morfismo identità che collega ogni elemento dell'oggetto a se stesso. E' una sorta di elemento neutro dei morfismi.
In una categoria la legge di composizione dei morfismi deve soddisfare la proprietà associativa.
Ad esempio, se considero tre morfismi: $$ f: A \rightarrow B $$ $$ g: B \rightarrow C $$ $$ h: C \rightarrow D $$ Queste due composizioni sono equivalenti $$ h \circ ( g \circ f ) = (h \circ g) \circ f $$
Un esempio pratico
In questo esempio costruisco una semplice categoria "Set" che comprende insiemi finiti, morfismi, una composizione di morfismi e delle identità.
Gli oggetti di questa categoria sono insiemi finiti. Ad esempio, tre insiemi:
$$ A = \{1, 2\}$$
$$ B = \{a, b, c\} $$
$$ C = \{\alpha, \beta\} $$
I morfismi in questa categoria sono tutte le possibili funzioni da un insieme all'altro. Ecco alcuni esempi di funzioni:
$$ f: A \rightarrow B $$
$$ f(1) = a \\ f(2) = b $$
$$ g: B \rightarrow C $$
$$ g(a) = \alpha \\ g(b) = \beta \\ g(c) = \alpha $$
Nota. In genere, per rappresentare una categoria si utilizza un diagramma o un grafo, in cui gli oggetti (insiemi) sono i nodi e le funzioni (morfismi) sono delle frecce tra i nodi. Le composizioni possono essere viste come percorsi nel diagramma. In generale i diagrammi topologici sono molto utili per visualizzare e comprendere le relazioni complesse.
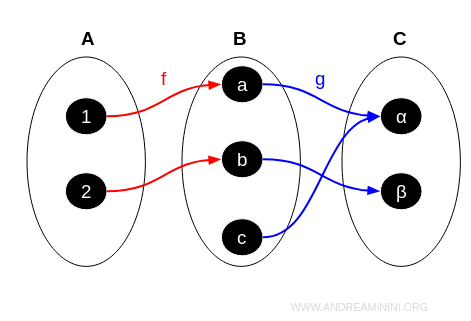
Da notare che il morfismo \( f: A \rightarrow B \) ha il codominio (B) che coincide con il dominio del morfismo \( g: B \rightarrow C \). In questo caso posso aggiungere alla categoria Set anche la composizione di morfismi\( f \) e \( g \))
La composizione dei morfismi segue la regola della composizione di funzioni.
$$ g \circ f: A \rightarrow C $$
$$ (g \circ f)(1) = g(f(1)) = g(a) = \alpha \\ (g \circ f)(2) = g(f(2)) = g(b) = \beta $$
In questo caso la composizione \( g \circ f \) è una funzione da \( A \) a \( C \) definita da \( (g \circ f)(x) = g(f(x)) \) per ogni \( x \) in \( A \).
Inoltre, per ogni insieme A, B, C della categoria Set deve esserci un morfismo identità \( \text{id}_X : X \rightarrow X \) che mappa ogni elemento a se stesso.
$$ \text{id}_A(1) = 1 \ \ \ \ \text{id}_A(2) = 2 $$
$$ \text{id}_B(a) = a \ \ \ \ \text{id}_B(b) = b \ \ \ \ \text{id}_B(c) = c $$
$$ \text{id}_C(\alpha) = \alpha \ \ \ \ \text{id}_C(\beta) = \beta $$
Questo esempio mostra una categoria concreta che è abbastanza semplice da comprendere ma sufficientemente ricca da illustrare i concetti di base della teoria delle categorie.
La struttura soddisfa tutte le proprietà di una categoria: associatività della composizione e l'elemento neutro dato dall'identità per ogni insieme.
E così via.
