I morfismi di una categoria

Nella teoria delle categorie i morfismi connettono gli oggetti all'interno di una categoria. $$ f_{AB}: A \rightarrow B $$ Dove A e B sono due oggetti mentre la freccia è il morfismo. L'oggetto A è detto dominio mentre l'oggetto B

I morfismi creano una struttura e stabiliscono delle relazioni tra oggetti della stessa categoria, in modi che preservano le proprietà essenziali degli oggetti coinvolti.

Ogni morfismo ha sempre una direzione dal dominio al codominio.

Ad esempio, il morfismo $ f_{AB} $ va dall'oggetto A all'oggetto B.

$$ f_{AB}: A \rightarrow B $$

Si distingue dal morfismo $ f_{BA} $ che invece collega gli stessi oggetti ma nel verso opposto, dall'oggetto B all'oggetto A.

$$ f_{BA}: B \rightarrow A  $$

Gli oggetti sono entità astratte e possono essere di qualsiasi tipo. Ad esempio, insiemi, gruppi, spazi vettoriali, matrici, ecc.

L'insieme di tutti i morfismi da un oggetto a un altro viene indicato con il simbolo hom. Ad esempio, tutti i morfismi dall'oggetto A all'oggetto B appartengono alla collezione $ hom(A,b) $ L'insieme di tutti i morfismi di una categoria è, invece, indicato con il simbolo mor(C) dove C è il nome della categoria.

In una categoria i morfismi devono soddisfare queste proprietà:

• Composizione di morfismi
  La composizione è una funzione composta da due morfismi $ f \in hom(A,B) $ e $ g \in hom(B,C)$ quando il codominio di f è uguale al dominio di g $$ f \circ g \in hom(A,C)$$

  Nota. La composizione di morfismi in una categoria soddisfa la proprietà associativa. Quindi, se ho tre morfismi vale la seguente relazione $$ f \circ (g \circ h) = (f \circ g) \circ h $$  Generalmente, la composizione di morfismi non è commutativa, il che significa che $ f \circ g \ne g \circ f $ nella maggior parte dei casi, a meno che non siano coinvolti specifici morfismi, come quelli identità o categorie particolari.

• Morfismo identità
  Ogni oggetto della categoria ha un morfismo identità che collega l'oggetto a se stesso e si comporta come l'elemento neutro del morfismo. $$ 1_A \in hom(A,A) $$ La composizione di un morfismo f con il morfismo identità equivale al morfismo f $$ f \circ 1_A = f $$

Un esempio pratico

Considero una categoria "Set" composta da insiemi.

Gli oggetti in questa categoria sono insiemi e i morfismi sono le funzioni tra questi insiemi.

Ad esempio, nella categoria ci sono tre insiemi:

$$ A = \{1, 2, 3\} $$

$$ B = \{a, b, c, d\} $$

$$ C = \{x, y\} $$

Per spiegare meglio le connessioni aggiungo una rappresentazione degli insiemi.

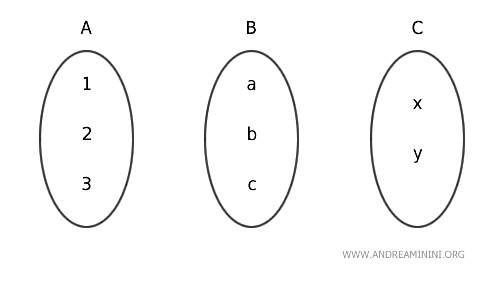
Per ipotesi, nella categoria "Set" ci sono due morfismi f e g:

$$ hom(A.B) = \{ f \} $$

$$ hom(B.C) = \{ g \} $$

Il morfismo $ f: A \rightarrow B $ è semplicemente una funzione che associa ogni elemento di \( A \) a un elemento di \( B \).

$$ f(1) = a $$

$$ f(2) = b $$

$$ f(3) = c $$

Il morfismo $ g: B \rightarrow C $ collega l'insieme B all'insieme C.

$$ g(a) = x $$

$$ g(b) = x $$

$$ g(c) = y $$

Rappresento i due morfismi f e g nel diagramma.

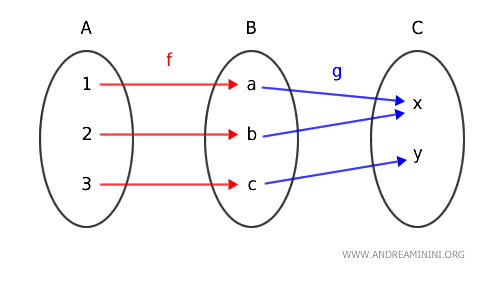
In questo caso il codominio del morfismo f coincide con il dominio del morfismo g.

Quindi posso comporre i due morfismi in una composizione di morfismi $ g \circ f : A \rightarrow C $

$$ g[f(1)] = g(a) = x $$

$$ g[f(2)] = g(b) = x $$

$$ g[f(3)] = g(c) = y $$ 

Di fatto la composizione aggiunge un altro morfismo tra due oggetti A e C della categoria "Set".

$$ hom(A.C) = \{ g \circ f \} $$

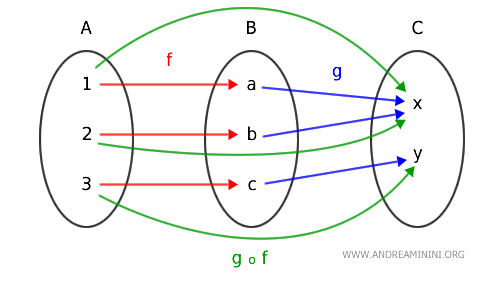
Per ogni insieme della categoria esiste anche un morfismo identità che mappa ogni elemento con se stesso.

$$ 1_A: A \rightarrow A $$

$$ 1_B: B \rightarrow B $$

$$ 1_C: C \rightarrow C $$

Ad esempio, il morfismi identità $ 1_A $ collega ogni elemento dell'insieme A a se stesso. $$ 1_A(1)=1 $$ $$ 1_A(2)=2 $$ $$ 1_A(3)=3 $$ Il morfismo identità $ 1_B $ collega ogni elemento dell'insieme B a se stesso $$ 1_B(a)=a $$ $$ 1_B(b)=b $$ $$ 1_B(c)=c $$ Infine, il morfismo $ 1_C $ collega ogni elemento dell'insieme C a se stesso $$ 1_C(x) = x $$ $$ 1_C(y) = y $$

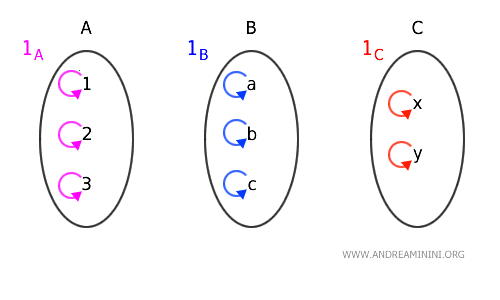
In conclusione, l'insieme di tutti i morfismi della categoria Set è composta dai morfismi diretti $ f,g $ dalla composizione $ g \circ f $ e dai morfismi identità $ 1_A, 1_B, 1_C $

$$ Mor(Set) = \{ f,g,g \circ f, 1_A, 1_B, 1_C \} $$

Questo esempio dovrebbe chiarire il concetto di morfismo nella categoria degli insiemi.

Osservazioni

Alcune osservazioni e note personali sui morfismi nella teoria delle categorie.

• Perché nella teoria delle categorie si parla di morfismi anziché di relazioni o funzioni?
  Nella teoria delle categorie, il termine "morfismo" viene utilizzato per diversi motivi che riflettono l'astrattezza e la generalità di questa branca della matematica. La teoria delle categorie usa il termine "morfismo" per enfatizzare un approccio più flessibile, astratto e strutturale alla descrizione delle relazioni matematiche, superando i limiti delle definizioni più tradizionali e rigide di funzione e relazione. Utilizzando il termine "morfismo", i matematici possono distaccarsi dalle connotazioni specifiche di termini come "relazione" o "funzione" che tradizionalmente implicano mappature dirette e ben definite tra elementi individuali di insiemi. I morfismi permettono di considerare anche mappature più complesse e meno dirette, inclusi cambiamenti strutturali o trasformazioni che non si limitano a una corrispondenza punto-per-punto.

  Ad esempio, i morfismi generalizzano il concetto di funzioni e mappature tra oggetti. Mentre in matematica tradizionale una funzione descrive una relazione specifica tra elementi di due insiemi, un morfismo in teoria delle categorie può descrivere operazioni molto più astratte e generali. Questo permette di incorporare sotto un unico discorso varie strutture matematiche, come insiemi, spazi, gruppi, anelli, e altro, ognuno con le proprie "funzioni" o "trasformazioni" che preservano la struttura interna degli oggetti.

  Inoltre, nella teoria delle categorie gli oggetti e i morfismi formano una struttura chiamata "categoria" e ogni categoria ha le sue regole specifiche su come i morfismi possono essere composti e come si relazionano agli oggetti. Quindi, l'uso del termine "morfismo" anziché "funzione" sottolinea l'importanza delle proprietà strutturali (come la composizione e l'identità) che devono essere soddisfatte.

  Esempio. Nella teoria delle categorie, una matrice 2×3 può essere considerata come un morfismo, ma non necessariamente in modo diretto come una "relazione" o "funzione" tradizionale tra insiemi di numeri. Una matrice 2x3 ha due righe e tre colonne, quindi può trasformare un vettore nello spazio vettoriale a 3 dimensioni (R³) in un vettore in un vettore nello spazio vettoriale a 2 dimensioni (R²). $$ f: R^3 \rightarrow R^2 $$ Tuttavia, questa "trasformazione" non implica nessuna relazione tra i numeri 2 e 3, quindi non può essere definita "funzione" tra i due numeri. E' più appropriato chiamarla morfismo. Per un approfondimento rimando a questo esempio.

E così via