La categoria preordinata nella teoria delle categorie

Una categoria preordinata è un tipo di categoria in cui esiste al massimo un solo morfismo diretto tra ogni coppia di oggetti e i morfismi hanno le proprietà delle relazioni di preordine.

In una categoria preordinata, i morfismi sono relazioni di preordine che soddisfano due proprietà fondamentali:

• Riflessiva: Ogni oggetto è relazionato a se stesso.
• Transitiva: Se un oggetto A è relazionato a un oggetto B, e B è relazionato a un oggetto C, allora A è relazionato a C.

Se c'è un morfismo da A a B, diciamo che A è minore o uguale a B e si indica con il simbolo A ≤ B.

Quindi, in pratica, una categoria preordinata può essere vista come una struttura dove gli oggetti sono ordinati in un certo modo, e l'ordine è determinato dall’esistenza stessa di morfismi tra di loro.

Nota. Il simbolo ≤ non è necessariamente il simbolo "maggiore-uguale" ma indica più in generale la relazione di preordine tra gli oggetti. In altre parole, potrebbe essere l'operatore maggiore-uguale in senso stretto o anche l'inclusione di un insieme in un altro, ecc.

Un esempio pratico

Considero un insieme di oggetti:

$$ S = (A, B, C, D) $$

Poi definisco dei morfismi tra gli oggetti:

$$ A \rightarrow A $$

$$ B \rightarrow B $$

$$ C \rightarrow C $$

$$ A \rightarrow B $$

$$ A \rightarrow C $$

$$ B \rightarrow D $$

$$ C \rightarrow D $$

$$ B \rightarrow C\ $$

$$ C \rightarrow B $$

Ora rappresento gli oggetti e morfismi della categoria in un diagramma.

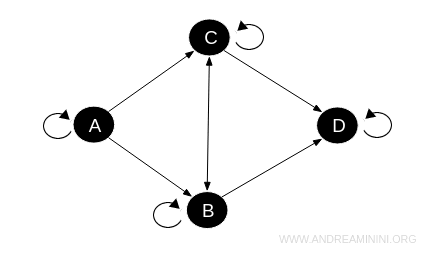
I morfismi della categoria soddisfano queste proprietà:

• Riflessività: Ogni oggetto è in relazione con se stesso (morfismo identità)
• Transitività: Se \(A \rightarrow B\) e \(B \rightarrow D\), allora \(A \rightarrow D\), e via dicendo

Non si tratta di una categoria poset (insieme parzialmente ordinato) perché l'antisimmetria non è necessaria.

Ad esempio, la relazione tra \(B\) e \(C\) è bidirezionale (\(B \rightarrow C\) e \(C \rightarrow B\)).

Cosa afferma la proprietà antisimmetrica? L'antisimmetria impone che tra due oggetti distinti non possa esserci una relazione reciproca. Secondo la proprietà antisimmetrica, se due oggetti sono in relazione reciproca, allora devono essere necessariamente lo stesso oggetto. L'antisimmetria non è necessaria in una categoria di preordine. Quindi, in una categoria di preordine due oggetti con una relazione reciproca possono essere anche diversi tra loro ovvero "equivalenti".

Pertanto, gli oggetti e morfismi definiscono una categoria preordinata.

La differenza tra categorie preordinata e categoria poset

Nella teoria delle categorie, le differenze tra una categoria preordinata e una categoria poset si basano sulla proprietà di antisimmetria.

• Categoria preordinata
  In una categoria preordinata esiste al massimo un morfismo esiste tra ogni coppia di oggetti. I morfismi sono relazioni di preordine, quindi soddisfano la riflessività e la transitività. Non è necessario che i morfismi siano anche antisimmetrici. In altre parole, la presenza di morfismi reciproci tra due oggetti \( A \) e \( B \) (ovvero da \( A \) a \( B \) e da \( B \) a \( A \)) non implica che \( A \) e \( B \) siano lo stesso oggetto; possono essere distinti ma considerati equivalenti.
  
• Categoria poset
  In una categoria poset (insieme parzialmente ordinato) i morfismi sono relazioni d'ordine. Quindi, soddisfano la proprietà riflessiva, transitiva e antisimmetrica. Questo vuol dire che se esistono morfismi reciproci tra due oggetti \( A \) e \( B \), allora \( A \) e \( B \) devono essere lo stesso oggetto. Anche in questo caso tra due oggetti può esserci al massimo un morfismo diretto.
  

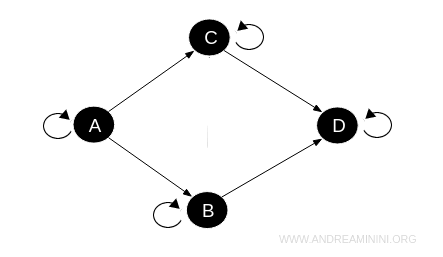
In conclusione, la scelta tra l'uso di una categoria preordinata o una categoria poset dipende dalla necessità di trattare equivalenze tra oggetti come identiche o solo funzionalmente simili.

E così via.