I funtori

Nella teoria delle categorie un funtore F  collega gli oggetti e i morfismi di due categorie diverse preservando le strutture interne delle categorie. $$ F: \text{Obj}(Cat_1 ) \rightarrow \text{Obj}(Cat_2) $$ $$ F: \text{Mor}(Cat_1 ) \rightarrow \text{Mor}(Cat_2) $$

Le categorie sono collezioni di oggetti e di morfismi (o frecce) tra questi oggetti. 

Un funtore F mappa ogni oggetto in una categoria a un oggetto in un'altra categoria, e ogni morfismo (freccia) in una categoria a un morfismo in un'altra categoria.

$$ F: \text{Obj}(Cat_1 ) \rightarrow \text{Obj}(Cat_2) $$

$$ F: \text{Mor}(Cat_1 ) \rightarrow \text{Mor}(Cat_2) $$

Dove Obj(Cat₁) e Obj(Cat₂) sono rispettivamente gli insiemi degli oggetti delle categorie Cat₁ e Cat₂, mentre Mor(Cat₁) e Mor(Cat₂) sono l'insieme dei morfismi delle due categorie.

Ad esempio, se il morfismo $ f: A \rightarrow B $ mappa gli oggetti A e B nella categoria 1 con gli oggetti F(A) e F(B) nella categoria 2, allora il morfismo $ F(f) : F(A) \rightarrow F(B) $ ottenuto tramite il funtore F mappa le immagini F(A) e F(B) nella categoria 2.

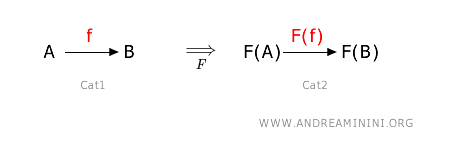
E' importante che questa mappatura rispetti la composizione dei morfismi.

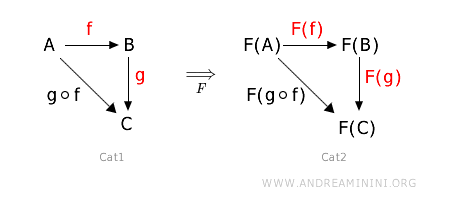
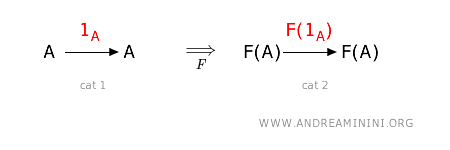
Inoltre, deve rispettare anche il morfismo identità degli oggetti.

Questo significa che l'immagine di un morfismo che compone due altri morfismi deve essere il morfismo che è la composizione delle immagini di quei due morfismi.

Quindi, il funtore preserva la "forma" delle relazioni tra oggetti nella categoria di origine all'interno della categoria di destinazione.

Nota. I funtori sono utili per trasferire problemi e soluzioni tra diverse categorie. In questo modo posso applicare metodi e intuizioni da un contesto all'altro in modo coerente e strutturato.

Covarianza e controvarianza

Un funtore collega i morfismi tra due categorie.

$$ F: \text{Mor}(Cat_1 ) \rightarrow \text{Mor}(Cat_2) $$

Tuttavia, questo collegamento tra i morfismi può avvenire in due modi distinti. I funtori possono essere covarianti o controvarianti.

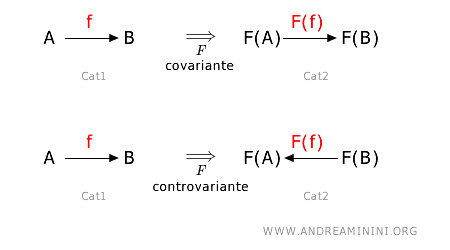
Nel caso dei funtori covarianti la direzione dei morfismi viene preservata mentre in quelli controvarianti viene invertita.

• Covarianti
   Il funtore covariante preserva la direzione dei morfismi. Se un morfismo va da A a B nella categoria di origine, allora il corrispondente morfismo va da F(A) a F(B) nella categoria di destinazione. $$ F: \text{hom}_{Cat1}(A,B) \rightarrow \text{hom}_{Cat2}(FA,FB) $$ Dove hom(A,B) è l'insieme dei morfismi dall'oggetto A all'oggetto B. Quindi, per ogni oggetto A e B nella categoria 1, se $f: A \rightarrow B $ è un morfismo nella categoria 1, allora $ F(f): F(A) \rightarrow F(B)  $ è il corrispettivo morfismo nella categoria 2. $$f: A \rightarrow B \ \ \  \underset{F}{ \Longrightarrow} \ \ \ F(f): F(A) \rightarrow F(B)  $$
  

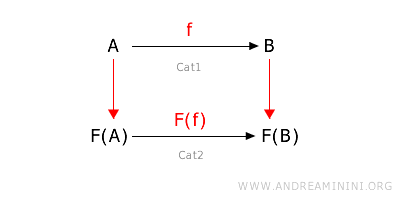
  Nota. I funtori covarianti sono naturali in molte trasformazioni dove voglio "seguire la direzione" delle funzioni originali, come trasformazioni geometriche o operazioni su strutture dati.

• Controvarianti
  Il funtore controvariante inverte la direzione dei morfismi. Se un morfismo va da A a B nella categoria di origine, allora il corrispondente morfismo va da F(B) a F(A) nella categoria di destinazione. $$ F: \text{hom}_{Cat1}(A,B) \rightarrow \text{hom}_{Cat2}(FB,FA) $$ Pertanto, per ogni oggetto A e B nella categoria 1, se $f: A \rightarrow B $ è un morfismo nella categoria 1, allora $ F(f): F(B) \rightarrow F(A)  $ è il corrispettivo morfismo nella categoria 2. $$f: A \rightarrow B \ \ \  \underset{F}{ \Longrightarrow} \ \ \ F(f): F(B) \rightarrow F(A)  $$ Da notare che la direzione è invertita rispetto ai funtori covarianti. In questo caso va da B ad A mentre nei funtori covarianti era sempre da A a B. 
  
  

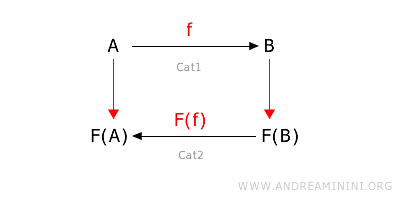
  Nota. I funtori controvarianti sono cruciali quando le operazioni o le relazioni devono essere "ribaltate", dove si considerano le pre-immagini piuttosto che le immagini.

Un esempio pratico

Per fare un esempio, considero due categorie: la categoria degli insiemi e la categoria delle liste.

Queste due categorie possono essere collegate tramite un funtore che trasforma ogni insieme in una lista.

Definisco il funtore "Lista".

• Oggetti: Ad ogni insieme \( A \) nella categoria degli insiemi, il funtore "Lista" associa la lista di tutti gli elementi di \( A \) nella categoria delle liste.

  Ad esempio, se \( A \) è l'insieme \( \{1, 2, 3\} \), allora \( F(A) \) potrebbe essere la lista [1, 2, 3].

• Morfismi: Ogni funzione \( f: A \to B \) tra gli insiemi viene mappata in una funzione \( F(f): F(A) \to F(B) \) tra le liste, dove \( F(f) \) applica \( f \) a ogni elemento della lista.

  Per esempio, se \( f(x) = x + 1 \) e \( A \) è \( \{1, 2, 3\} \), allora \( F(f) \) applicata a [1, 2, 3] produrrà [2, 3, 4].

Il funtore "Lista" preserva la struttura interna delle categorie. In particolar modo:

• Preserva le composizioni nelle categorie
  Se ci sono due funzioni/morfismi \( f: A \to B \) e \( g: B \to C \) in una categoria, allora il funtore "Lista" preserva la composizione anche tra le liste \( F(g \circ f) = F(g) \circ F(f) \). Ovviamente, a seconda se il funtore è covariante o controvariante.
  
  Se il funtore è covariante $$ F(g \circ f) = F(g) \circ F(f) $$ Se il funtore è controvariante $$ F(g \circ f) = F(f) \circ F(g) $$
• Preserva l'identità
  La funzione identità su un insieme \( A \) è mappata nella funzione identità sulla lista \( F(A) \).$$ F \ 1_A = 1_{FA} $$
  

  Ad esempio, se \( \text{id}_A \) è la funzione identità su \( A = \{1,2,3 \} \), allora \( F(\text{id}_A) \) è la funzione identità su [1, 2, 3], che lascia ogni elemento inalterato.

Il funtore "Lista" trasforma ogni operazione su singoli elementi in un'operazione su una struttura di dati più complessa come una lista.

Nota. Questo tipo di funtore è comune nei linguaggi di programmazione funzionale, dove le strutture di dati e le funzioni possono essere manipolate in modo molto generale e potente.

Esempio 2

In questo esempio analizzo un funtore che mappa la categoria degli insiemi con la categoria degli insiemi potenza.

1. Categoria degli insiemi
   E' la categoria dove gli oggetti sono insiemi e i morfismi sono funzioni tra questi insiemi.
2. Categoria degli insiemi potenza
   E' la categoria dove ogni oggetto è l'insieme potenza di un insieme, ovvero l'insieme di tutti i sottoinsiemi di quell'insieme, e i morfismi sono funzioni tra questi insiemi potenza.

Definisco un funtore  `P` che mappa ogni insieme al suo insieme potenza:

Questo tipo di funtore trasforma insiemi in insiemi potenza e funzioni in funzioni tra insiemi potenza.

• Oggetti: Per ogni insieme \( A \), \( P(A) \) è l'insieme potenza di \( A \).

  Ad esempio, se \( A \) è l'insieme \( \{1, 2\} \), allora il suo insieme potenza \( P(A) \) sarà \( \{\{\}, \{1\}, \{2\}, \{1, 2\}\} \).

• Morfismi: Ogni funzione \( f: A \to B \) viene trasformata in una funzione \( P(f): P(A) \to P(B) \) che mappa ogni  sottoinsieme di \( A \) nel sottoinsieme di \( B \) ottenuto applicando \( f \) a ciascun elemento del sottoinsieme.

  Ad esempio, se \( f(x) = x + 1 \) e \( A \) è \(  \{1, 2\} \), allora:
  \( P(f)(\{\}) = \{\} \)
  \( P(f)(\{1\}) = \{2\} \)
  \( P(f)(\{2\}) = \{3\} \)
  \( P(f)(\{1, 2\}) = \{2, 3\} \)

Come al solito il funtore preserva la struttura interna delle categorie:

• Composizione di morfismi: Se ci sono due morfismi \( f: A \to B \) e \( g: B \to C \), allora anche la composizione di morfismi è  \( P(g \circ f) = P(g) \circ P(f) \).

  Questo significa che applicare \( g \) dopo \( f \) a ogni elemento di un sottoinsieme di \( A \) è equivalente a applicare prima \( P(f) \) e poi \( P(g) \) al risultato.

• Morfismo identità: Se \( \text{id}_A \) è il morfismo identità su \( A \) allora \( P(\text{id}_A) \) è il morfismo identità su \( P(A) \)

A questo punto introduco anche i concetti di funtori covarianti e controvarianti.

Nella categoria degli insiemi ipotizzo che ci sia un morfismo \( f: A \to A \) definito come \( f(x) = 3 - x \)

Ad esempio, se considero l'insieme \( A = \{1, 2\} \) allora il morfismo collega ogni oggetto a un altro. In questo caso \( f(1) = 2 \) e \( f(2) = 1 \).

Il funtore covariante 'P' mappa gli oggetti e i morfismi dell'insieme nel corrispondente insieme potenza.

• Oggetti: Mappa \( A \) a \( P(A) \), dove \( P(A) = \{\{\}, \{1\}, \{2\}, \{1, 2\}\} \).
• Morfismi: \( P(f): P(A) \to P(A) \), definito da \( P(f)(S) = \{f(x) | x \in S\} \).

Ecco alcuni esempi di mappatura ottenuti con P(f)

\( P(f)( \{ \} ) = \{ \} \)
\( P(f)(\{1\}) = \{2\} \)
\( P(f)(\{2\}) = \{1\} \)
\( P(f)(\{1, 2\}) = \{2, 1\} = \{1, 2\} \)

Quindi, il funtore covariante `P` conserva la struttura delle operazioni applicando la funzione \( f \) a ciascun elemento dell'insieme. Questo riflette la mappatura dell'elemento nell'insieme originale all'elemento nell'insieme destinazione.

Il funtore covariante `Q` invece mappa ogni insieme al suo insieme potenza ma inverte la direzione delle funzioni.

• Morfismi: \( Q(f): Q(A) \to Q(A) \) è definito da \( Q(f)(T) = \{x | f(x) \in T\} \).

Ecco alcuni esempi di mappatura di Q(f)

\( Q(f)(\{\}) = \{\} \) (nessun elemento ha una immagine in \{\})
\( Q(f)(\{1\}) = \{2\} \) (solo 2 è mappato in 1 da \( f \))
\( Q(f)(\{2\}) = \{1\} \) (solo 1 è mappato in 2 da \( f \))
\( Q(f)(\{1, 2\}) = \{1, 2\} \) (entrambi gli elementi sono mappati in \{1, 2\} da \( f \))

Il funtore controvariante `Q` inverte la direzione della funzione, considerando la preimmagine degli elementi rispetto alla funzione originale.

Questo mostra come gli elementi originali contribuiscano alla formazione del sottoinsieme nell'insieme destinazione.

In questo esempio, `P` (covariante) applica direttamente la funzione agli elementi dell'insieme, mentre `Q` (controvariante) considera come gli elementi dell'insieme destinazione siano stati ottenuti dagli elementi dell'insieme originale, effettuando una mappatura inversa rispetto alla funzione data.

Questi esempi mostrano come i funtori possano essere usati per trasformare e trasferire strutture tra categorie in maniere che conservano o invertono la direzione delle operazioni originarie.

Spero che questo esempio renda più chiaro il concetto di funtore.

E così via.