La categoria dei gruppoidi
La categoria gruppoide è una categoria in cui ogni morfismo è un isomorfismo, quindi ogni morfismo è invertibile, e ha le proprietà di una relazione di equivalenza.
In una categoria gruppoide ogni morfismo è un isomorfismo, il che significa che ogni morfismo ha un inverso.
Questa proprietà implica che ogni relazione tra oggetti nella categoria è essenzialmente una relazione di equivalenza, ovvero soddisfa queste proprietà:
- Riflessività: Ogni oggetto ha un morfismo identità che lo mappa su se stesso
- Simmetria: Per ogni morfismo che mappa un oggetto \(a\) su un oggetto \(b\), esiste un morfismo inverso che mappa \(b\) su \(a\)
- Transitività: Se esiste un morfismo da \(a\) a \(b\) e un altro da \(b\) a \(c\), allora esiste anche un morfismo composito da \(a\) a \(c\)
Quindi, in un gruppoide ogni oggetto ha una relazione riflessiva con se stesso attraverso l'identità, crea una relazione simmetrica attraverso il suo inverso, e la composizione di morfismi garantisce la transitività.
In un gruppoide, possono esistere anche più morfismi tra due oggetti, purché ogni morfismo possa essere invertito.
A differenza della categoria preordinata e della categoria dei poset, nella categoria gruppoide non è necessario che ci sia al massimo un morfismo tra due oggetti. Ciò che caratterizza un gruppoide non è l'unicità dei morfismi tra gli oggetti, ma il fatto che ogni morfismo è un isomorfismo, il che significa che ogni morfismo ha un inverso.
Un esempio pratico
Prendo come esempio il gruppoide delle simmetrie di un oggetto geometrico. Ad esempio, un quadrato.
In questa categoria gruppoide:
- Gli oggetti sono i punti del quadrato
- I morfismi sono le trasformazioni che portano un punto in un altro mantenendo l'integrità del quadrato. Queste trasformazioni includono le rotazioni di 90, 180, 270 gradi e la riflessione sugli assi.
In questa categoria ogni morfismo ha un inverso.
Ad esempio, la rotazione di 90 gradi in senso orario ha come inverso la rotazione di 270 gradi in senso orario (o 90 gradi in senso antiorario).
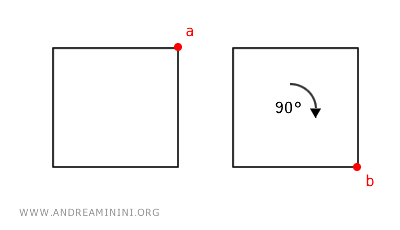
Inoltre, posso ottenere lo stesso morfismo tra ogni coppia di punti $ a $ e $ b $ facendo una rotazione di 360°+90°. Il risultato è lo stesso di una rotazione di 90° e via dicendo.
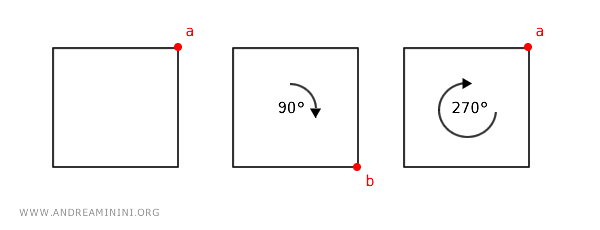
La caratteristica chiave qui è che ogni trasformazione può essere invertita, e ci possono essere molteplici modi per trasformare un punto in un altro attraverso diverse combinazioni di rotazioni e riflessioni.
Questo esempio dimostra che in una categoria gruppoide, a differenza di un poset, può effettivamente esistere più di un morfismo tra due oggetti, purché ogni morfismo possa essere annullato da un altro.
E così via.
