La categoria dei poset nella teoria delle categorie

La categoria dei poset (partially ordered set) è una categoria in cui esiste al massimo un morfismo diretto $ a \rightarrow b $ tra due oggetti $ a, b $ dell'insieme P e i morfismi hanno le proprietà delle relazioni d'ordine

In generale, un poset (insiemi parzialmente ordinati) è un insieme $P$ con una relazione di ordine $\leq$ che è riflessiva, antisimmetrica e transitiva.

$$ Poset (P, \leq) $$

Questo significa che per ogni coppia di elementi $a$ e $b$ in $P$

ogni elemento è uguale a se stesso $ a = a $ (riflessività)
se $a \leq b$ e $b \leq a$, allora $a = b$ (antisimmetria)
se $a \leq b$ e $b \leq c$, allora $a \leq c$ (transitività).

I poset hanno tutte le caratteristiche per essere considerati una categoria ($P, \leq$)

Oggetti
In questa categoria, gli oggetti sono gli elementi dell'insieme $P$.
Morfismi
I morfismi (funzioni) tra due oggetti $a,b \in P $ esistono solo se $a \leq b$. Se $a \leq b$, allora c'è un unico morfismo diretto da $a$ a $b$, ovvero una relazione d'ordine tra $a$ e $b$. Ogni relazione d'ordine soddisfa la proprietà associativa.
Nota. Come accade anche in altre categorie, tutti i morfismi tra due oggetti appartengono all'insieme hom(a, b). In generale, tutti i morfismi dell'insieme $ P $ appartengono all'insieme $ Mor(P) $.
Composizione dei morfismi
Se ci sono morfismi da $a$ a $b$ e da $b$ a $c$, che implica $a \leq b$ e $b \leq c$, allora deve esistere un morfismo diretto da $a$ a $c$, dato che $a \leq c$ per la transitività dell'ordine. Questo morfismo è unico.
Morfismo identità
Poiché la relazione d'ordine è riflessiva, ogni elemento $ a \in P $ dell'insieme poset ha un morfismo identità per definizione.

Quindi, un insieme parzialmente ordinato (poset) soddisfa tutte le caratteristiche di una categoria.

In generale, la teoria delle categorie applicata ai poset mi fornisce un modo molto strutturato e astratto di considerare le relazioni d'ordine tra gli elementi di un insieme parzialmente ordinato.

Un esempio pratico

Ogni singolo numero naturale $ n \in \mathbb{N} $ posso vederlo come un insieme che contiene tutti i numeri naturali minori di $n$, da $0$ fino a $n-1$.

$$ \mathbb{N} = \{ 0,1,2,3,4,5,... \} $$

Dove il numero naturale $0$ è definito come l'insieme vuoto $ \emptyset $ perché non ha predecessori.

$$ 0 = \{ \} $$

Il numero naturale $ 1 $, invece, è definito come un insieme con un solo elemento, perchè ha come predecessore il numero $ 0 $.

$$ 1 = \{ 0 \} $$

Il numero naturale $ 2 $ ha due predecessori $ 0 $ e $ 1 $ ed è definito come un insieme formato da due elementi. E via dicendo.

$$ 2 = \{ 0,1 \} $$

Quindi, ogni singolo numero naturale definisce una categoria dove gli oggetti sono i numeri minori di sé, e i morfismi rappresentano l'ordine naturale o la relazione d'inclusione tra questi numeri.

Ad esempio, prendo il numero naturale $ n = 3 $ ed esploro la sua struttura come una categoria.

Il numero 3 come categoria è definito come l'insieme di tutti i numeri naturali che lo precedono:

$$ 3 = \{0, 1, 2\} $$

In questa categoria gli oggetti sono i numeri $ 0 $, $ 1 $, e $ 2 $ ovvero i predecessori di 3.

I morfismi sono definiti dalla relazione di ordine naturale ($\leq$), dove un morfismo esiste da un numero a un altro se e solo se il primo è minore o uguale al secondo.

Ecco l'elenco dei morfismi in questa categoria:

$$ id_0: 0 \rightarrow 0 $$

$$ id_1: 1 \rightarrow 1 $$

$$ id_2: 2 \rightarrow 2 $$

$$ f: 0 \rightarrow 1 $$

$$ g: 0 \rightarrow 2 $$

$$ h: 1 \rightarrow 2 $$

I primi tre sono morfismi identità, perché ogni elemento dell'insieme $ \{ 0,1,2 \} $ è in relazione d'ordine $ \leq $ con se stesso perché $ 0 \leq 0 $, $ \ \leq 1 $, $ 2 \leq 2 $.

Gli altri tre morfismi, invece, sono relazioni d'ordine $ \leq $ tra oggetti diversi della categoria: $ 0 \leq 1 $, $ 0 \leq 2 $ e $ 1 \leq 2 $.

Quindi, gli insiemi home-set dei morfismi della categoria sono i seguenti:

hom(0, 0): Contiene solo l'identità di $ 0 $, $ \text{id}_0 $.
hom(1, 1): Contiene solo l'identità di $ 1 $, $ \text{id}_1 $.
hom(2, 2): Contiene solo l'identità di $ 2 $, $ \text{id}_2 $.
hom(0, 1): Contiene un morfismo, diciamo $ f $, che rappresenta $ 0 \leq 1 $.
hom(0, 2): Contiene un morfismo, diciamo $ g $, che rappresenta $ 0 \leq 2 $.
hom(1, 2): Contiene un morfismo, diciamo $ h $, che rappresenta $ 1 \leq 2 $.

Nota. Gli insiemi hom(1, 0), hom(2, 0) e hom(2, 1) sono insiemi vuoti perché non c'è una relazione di ordine che va da un numero maggiore a uno minore. In altre parole, nella categoria 3 non ci sono morfismi da 1 a 0, da 2 a 0 e da 2 a 1.

Considerando i morfismi f, g posso costruire la composizione di un morfismo.

Il morfismo $ f $ composto con $ h $ dà $ g $.

$$ h \circ f = g $$

Dove $ f $ rappresenta un morfismo da $ 0 $ a $ 1 $ mentre $ h $ rappresenta un morfismo da $ 1 $ a $ 2 $.

Il risultato finale è il morfismo $ g $ che rappresenta un morfismo da $ 0 $ a $ 2 $.

Questo riflette la transitività dell'ordine naturale: se $ 0 \leq 1 $ e $ 1 \leq 2 $, allora $ 0 \leq 2 $.

Nota. La composizione dei morfismi di $ f $ e $ h $ si scrive come $ h \circ f $ e il morfismo più interno va calcolato prima del morfismo più esterno, ossia prima $ f $ e poi $ h $. Questo significa che applicando prima $ f $ e poi $ h $, si ottiene $ g $, rispecchiando la transitività della relazione di ordine in $ P $ dove $ 0 \leq 1 \leq 2 $ implica $ 0 \leq 2 $.

Riepilogando, posso rappresentare la categoria graficamente in questo modo:

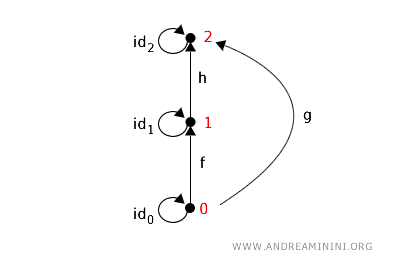
il diagramma della categoria

In questo diagramma, le frecce rappresentano i morfismi, indicando una relazione di ordine ascendente.

L'insieme di tutti i morfismi della categoria è composto da 3 morfismi:

$$ Mor(3) = \{ id_0, id_1, id_2, f, g, h \} $$

In conclusione, questo esempio dimostra come un insieme di numeri naturali minori di un dato numero possa essere strutturato come una categoria, con oggetti e morfismi che rispecchiano le relazioni di ordine naturale.

Gli elementi $ n $ rappresentano gli oggetti, e le relazioni di ordine ($\leq$) tra di essi formano i morfismi.

E così via.