Le operazioni tra numeri interi

Nell'insieme dei numeri interi Z si possono utilizzare le seguenti operazioni

Addizione

Dati due numeri interi a e b la somma di due numeri interi è un numero intero c=a+b $$ c=a+b $$

Per calcolare la somma di due numeri interi occorre distinguere se i numeri sono concordi o discordi, ossia hanno lo stesso segno oppure no.

• Somma di numeri concordi
  La somma di due numeri interi concordi è uguale alla somma dei valori assoluti dei due addendi e ha lo stesso segno dei due addendi.

  Esempio. $$ 2+3 = + (|2|+|3|) + (2+3) = + 5 $$

• Somma di numeri discordi
  La somma di due numeri interi discordi è uguale alla differenza tra il valore assoluto maggiore e il valore assoluto minore dei due addendi e il segno del valore assoluto maggiore.

  Esempio. $$ -3+5 = + (|5|-|-3|) = + (5-3) = + 2 $$

L'addizione è un'operazione interna nell'insieme dei numeri interi perché la somma di due numeri interi è sempre un altro numero intero.

La somma tra due numeri interi soddisfa la proprietà commutativa e associativa.

$$ a+b=b+a $$

$$ a+(b+c)=(a+b)+c $$

Il numero zero è l'elemento neutro dell'addizione perché la somma di un numero intero e zero è sempre uguale al numero stesso.

$$ a+0=0+a=a$$

Sottrazione

La differenza tra due numeri interi a-b è uguale alla somma algebrica tra il minuendo (a) e l'opposto del sottraendo (-b) $$ a-b = a+(-b) $$ Il risultato della sottrazione è detto differenza.

La sottrazione è l'operazione inversa dell'addizione

Esempio. La sottrazione tra i numeri interi 23-14 $$ 23 - 14 $$ posso riscriverla come somma algebrica tra il minuendo (23) e l'opposto del sottraendo (-14) $$ 23 + (-14) $$ A questo punto per calcolare il risultato applico le stesse regole già viste per l'addizione. $$ 23 + (-14) = +9 $$ La differenza è +9

La sottrazione è un'operazione interna nell'insieme dei numeri interi perché la differenza di due numeri interi è sempre un numero intero.

$$ \forall \ a,b \in Z \Rightarrow a-b \in Z $$

Nota. La sottrazione non è invece una operazione interna nell'insieme dei numeri naturali (N) perché la differenza tra due interi può anche essere un numero intero negativo Z^- e i numeri interi negativi non appartengono all'insieme dei numeri naturali N. $$ 14 - 23 = 14 + (-23) = -9 \notin N $$ Pertanto, nel caso dei numeri naturali il minuendo deve essere maggiore del sottraendo. Questa condizione non vale, invece, per i numeri interi Z.

La differenza tra due numeri interi soddisfa la proprietà invariantiva.

Sommando o sottraendo lo stesso valore (c) dal minuendo (a) e dal sottraendo (b) la differenza a-b non cambia.

$$ a-b = (a+c) - (b+c) $$

$$ a-b = (a-c) - (b-c) $$

Moltiplicazione

Il prodotto tra due numeri interi a*b è un numero intero uguale al prodotto dei valori assoluti dei fattori che ha segno positivo (+) se i fattori sono concordi o segno negativo (-) se i numeri sono discordi.

La regola dei segni nella moltiplicazione è molto semplice.

Spesso è sintetizzata in questa tabella.

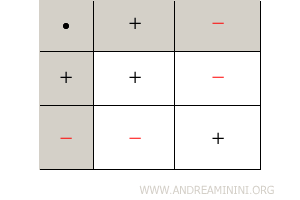
Esempio. Nel prodotto tra 3 e -4 $$ 3 \cdot (-4) $$ i due numeri hanno segno diverso, ossia sono discordi, quindi il prodotto ha segno meno. $$ - (|3| \cdot |-4|) = - (3 \cdot 4) = - 12 $$

La regola dei segni vale anche se i fattori nella moltiplicazione sono più di due.

In questo caso il segno del prodotto è sempre positivo se il segno meno nei fattori si ripete un numero pari di volte.

Viceversa, il segno del prodotto è negativo.N

Esempio. Nel prodotto tra 3, -4 e -2 il segno meno si ripete un numero pari di volte, quindi il prodotto ha segno positivo. $$ + (|3| \cdot |-4| \cdot |-2|) = + (3 \cdot 4 \cdot 2) = - 24 $$

La moltiplicazione è un'operazione interna nell'insieme dei numeri interi (Z) perché il prodotto di due numeri interi è ancora un numero intero.

$$ \forall \ a,b \in Z \Rightarrow a \cdot b \in Z $$

La moltiplicazione dei numeri interi soddisfa la proprietà commutativa

$$ a \cdot b = b \cdot a $$

Esempio. Il prodotto tra 2 e -4 è uguale al prodotto tra -4 e 2 $$ 2 \cdot (-4) = (-4) \cdot 2 = - 8 $$

La moltiplicazione dei numeri interi soddisfa la proprietà associativa

$$ a \cdot ( b \cdot c) = (b \cdot a) \cdot c $$

Esempio. Il prodotto tra -2 e (4·3) è uguale al prodotto tra (-2·4) e 2 $$ -2 \cdot (4 \cdot 3) = (-2 \cdot 4) \cdot 3 = - 24 $$

La moltiplicazione dei numeri interi soddisfa la proprietà distributiva rispetto all'addizione.

$$ a \cdot ( b + c) = a \cdot b + a \cdot c $$

Esempio. Il prodotto tra -2 e (4+3) è uguale alla somma dei prodotti -2·4 e -2·3 $$ -2 \cdot (4 + 3) = -2 \cdot 4 + (-2) \cdot 3 = - 14 $$

L'elemento neutro della moltiplicazione è il numero intero +1.

Il prodotto di qualsiasi numero intero per +1 è uguale al numero stesso

$$ \forall \ a \in Z \Rightarrow a \cdot 1 = a $$

Esempio. Il prodotto tra 4 e +1 è uguale a 4. $$ 4 \cdot 1 = +( |4| \cdot |1| ) = + (4 \cdot 1) = 4 $$

Viceversa, la moltiplicazione di qualsiasi numero intero per il numero -1 permette di ottenere il suo numero opposto.

$$ \forall \ a \in Z \Rightarrow a \cdot (-1) = -a $$

Esempio. Il prodotto tra 4 e -1 è uguale a -4 ossia al valore opposto di 4. $$ 4 \cdot (-1) = - ( |4| \cdot |-1| ) = - (4 \cdot 1) = -4 $$

L'elemento assorbente della moltiplicazione è il numero 0, perché il prodotto di qualsiasi numero intero per zero è uguale all'elemento assorbente stesso ossia a zero.

$$ \forall \ a \in Z \Rightarrow a \cdot 0 = 0 \cdot a = 0 $$

Pertanto, nella moltiplicazione dei numeri interi vale la legge di annullamento del prodotto.

Esempio. Il prodotto tra 4 e 0 è uguale a zero. $$ 4 \cdot 0 = 0 \cdot 4 = 0 $$

Divisione

La divisione tra due numeri interi a e b con b diverso da zero è un numero razionale detto quoziente. $$ a:b = q \in Q $$ dove a è detto dividendo e b è detto divisore.

La divisione è l'operazione inversa della moltiplicazione.

Se il numero dividendo a=k·b è un multiplo del divisore, il quoziente è un numero intero.

$$ \forall \ a,b,k \in Z \ , \ a=k \cdot b \ \Rightarrow a:b=(k \cdot b):b = k \in I $$

In generale, il risultato della divisione tra due interi a:b con b≠0 è uguale al quoziente dei valori assoluti dei due numeri |a|:|b| e il segno deciso dalle regole del segno della moltiplicazione.

Quindi, l'operazione di calcolo è molto simile alla moltiplicazione.

Esempio. La divisione tra 8 e -2 è il numero intero -4 $$ \frac{8}{-2} = - ( \frac{|8|}{-2} ) = - ( \frac{8}{2} ) = - 4 $$ Il dividendo ha segno positivo mentre il divisore ha segno negativo. I due numeri sono discordi, quindi il quoziente ha segno meno.

La divisione soddisfa la proprietà invariantiva.

Moltiplicando o dividendo per uno stesso numero diverso da zero k≠0 sia il dividendo che il divisore, il quoziente non cambia.

$$ a:b = (a \cdot k):(b \cdot k) $$

Forse, usando le frazioni quest'ultimo concetto si comprende meglio

$$ \frac{a}{b} = \frac{a}{b} \cdot 1 = \frac{a}{b} \cdot \frac{k}{k} = \frac{a \cdot k}{b \cdot k} $$

Esempio. Il quoziente della divisione 8:2 è 4. $$ \frac{8}{2} = 4 $$ Se moltiplico per k=3 il dividendo e il divisore il quoziente è sempre 4. $$ \frac{8 \cdot 3}{2 \cdot 3} = \frac{24}{6} = 4 $$

La divisione soddisfa la proprietà distributiva dell'addizione a destra.

$$ (a+b):c = a:b + b:c $$

Esempio. La divisione di (6+2) diviso 2 $$ (6+2):2 = 8:2 = 4 $$ posso calcolarla applicando la proprietà distributiva a destra dell'addizione. $$ (6+2):2 = 6:2 + 2:2 = 3 + 1 = 4 $$

Non soddisfa però la proprietà distributiva dell'addizione a sinistra

$$ c:(a+b) \ne c:a + c:b $$

Esempio. La divisione tra 12 e (4+2) è uguale a 2 $$ 12:(4+2) = 12:6 = 2 $$ non si può calcolare usando la proprietà distributiva a sinistra dell'addizione. $$ 12:(4+2) = 2 \ne 12:4 + 12:2 = 3 + 6 = 9 $$

La divisione non è un'operazione interna nell'insieme dei numeri interi perché il quoziente può anche essere un numero razionale.

$$ \forall \ a,b \in Z \ , \ b \ne 0 \Rightarrow a:b \in Q $$

Inoltre, se il dividendo è zero il quoziente è indeterminato (es. 0:0) oppure impossibile (es. 5:0).

Esempio. La divisione tra 5 e 2 è uguale a 2,5 $$ 5:2=2,5 $$ Il quoziente non è un numero intero (Z). $$ 2,5 \notin Z $$ E' un numero razionale (Q). $$ 2,5 \in Q $$

L'elemento neutro della divisione è il numero 1 perché qualsiasi numero intero diviso per 1 è uguale al numero stesso.

$$ \forall \ a \in Z \Rightarrow a:1 = a $$

Esempio. La divisione tra 4 e 1 è uguale a 4 $$ 4:1 = 4 $$ La divisione tra -4 e 1 è uguale -4 $$ -4:1 = -4 $$

Pertanto, qualsiasi numero intero diviso per se stesso è uguale a 1

$$ \forall \ a \in Z \Rightarrow a:a = 1 $$

Esempio. La divisione tra 4 e 4 è uguale a 1 $$ 4:4 = 1 $$ La divisione tra -4 e -4 è uguale a 1 $$ (-4):(-4) = 1 $$

Qualsiasi numero diviso intero per -1 è uguale al numero opposto.

$$ \forall \ a \in Z \Rightarrow a:(-1) = -a $$

Esempio. La divisione tra 4 e -1 è uguale a -4 $$ 4:(-1) = -4 $$ La divisione tra -4 e -1 è uguale a 4 $$ (-4):(-1) = 4 $$

Potenza

La potenza di un numero intero diverso da zero a≠0 con esponente naturale n è uguale in valore assoluto alla potenza del valore assoluto della base e ha come segno


• segno negativo (-) se la base è negativa e l'esponente è dispari
• segno positivo (+) negli altri casi

Il segno della potenza segue la regola del segno della moltiplicazione.

Esempio. Calcolo la potenza di -3 alla quinta $$ (-3)^5 $$ La base (-3) è negativa e l'esponente è dispari (5), quindi il segno della potenza è negativo (-). $$ (-3)^5 = - ( |-3| )^5 = - (3^5) = - 243 $$ Lo stesso risultato lo posso ottenere usando la regola del segno della moltiplicazione $$ (-3)^5 = (-3) \cdot (-3) \cdot (-3) \cdot (-3) \cdot (-3) = - 243 $$ Il segno meno si presenta un numero dispari di volte nel prodotto, quindi la potenza è negativa.

Nel caso particolare in cui la base della potenza è zero, la potenza con esponente intero positivo è sempre uguale a zero.

$$ 0^n = 0 \ \ \ con \ n \in Z \ , \ n>0 $$

Se l'esponente è uguale a 1 la potenza di un numero intero è sempre uguale al numero stesso.

$$ \forall \ a \in Z \Rightarrow a^1 = a $$

Esempio. La potenza di 4¹ è uguale a quattro $$ 4^1 = 4 $$

Se l'esponente è uguale a -1 la potenza di un numero intero diverso da zero è uguale al suo reciproco

$$ \forall \ a \in Z \ , \ a \ne 0 \Rightarrow a^{-1} = \frac{1}{a} $$

Esempio. La potenza di 4^-1 è uguale a 1/4 $$ 4^{-1} = \frac{1}{4^1} = \frac{1}{4} $$

Se l'esponente è uguale a 0 e la base è diversa da zero la potenza è uguale a 1.

$$ \forall \ a \in Z \ , \ a \ne 0 \Rightarrow a^0 = 1 $$

Per un approfondimento vedi dimostrazione.

Esempio. La potenza di 4⁰ è uguale a 1 $$ 4^0 = 1 $$

Se l'esponente è uguale a 0 e la base è uguale a zero, la potenza non è definita (indeterminata)

$$ 0^0 = \ indeterminata $$

Per un approfondimento vedi dimostrazione.

Se la base è uguale a zero e l'esponente è un numero intero positivo (numero naturale), la potenza è sempre uguale a zero

$$ \forall \ n \in Z \ , \ n>0 \Rightarrow 0^n = 0 $$

Esempio. La potenza di 0³ è uguale a zero perché qualsiasi moltiplicazione per zero è uguale a zero. $$ 0^3 = 0 \cdot 0 \cdot 0 = 0 $$

Se la base è uguale a zero e l'esponente è un intero negativo, la potenza è un'operazione impossibile

$$ \forall \ n \in Z \ , \ n<0 \Rightarrow 0^n = impossibile $$

Esempio. La potenza di 0^-1 equivale a una divisione per zero $$ 0^{-1} = \frac{1}{0^1} = impossibile $$

C'è un aspetto particolare che, secondo me, inizialmente può trarre in inganno e vale la pena sottolinearne l'importanza.

La potenza ha sempre la precedenza sul segno se il numero con il segno è senza parentesi.

Esempio. Nel caso (-4)² la potenza va applicata alla base -4 $$ (-4)^2 = (-4) \cdot (-4) = 16 $$ Viceversa nel caso -4² la potenza va applicata alla base 2 perché la potenza ha la precedenza sul segno. In questo caso la base è 4, non è -4 $$ -4^2 = - ( 4 \cdot 4 ) = - 16 $$ Pertanto, le due espressioni non danno lo stesso risultato $$ (-4)^2 \ne -4^2 $$

E così via.