La soluzione dei sistemi lineari con Gauss Jordan
Un sistema lineare può essere risolto utilizzando il metodo di eliminazione Gauss-Jordan sulla matrice completa A|B del sistema di equazioni.
Come risolvere un sistema lineare con Gauss-Jordan
La matrice A|B viene trasformata in una matrice a scalini tramite le operazioni di Gauss-Jordan.
Perché? Un sistema lineare a gradini si risolve molto facilmente anche se è composto da numerose equazioni e variabili incognite.
In base al numero dei pivot si può calcolare il rango della matrice dei coefficienti A e della matrice completa A|B.

Nota. Secondo il metodo del calcolo del rango di Gauss il numero dei pivot di una matrice a gradini eguaglia il rango della matrice.
Dal rango delle matrici è possibile verificare l'esistenza delle soluzioni del sistema tramite il teorema di Rouché-Capelli.
Se il sistema ammette soluzioni ed è rettangolare, vanno parametrizzate le variabili nelle colonne della matrice dei coefficienti A prive di numeri pivot.
Nota. L'ultima colonna della matrice completa A|B non va parametrizzata, in quanto identifica i termini noti del sistema di equazioni.
Nella forma parametrizzata la matrice dei coefficienti diventa una matrice quadrata.

Pertanto, le soluzioni del sistema possono essere trovate utilizzando il metodo di Cramer oppure sono già visibili.
Un esempio pratico
Dato un sistema lineare con tre equazioni e quattro variabili incognite:
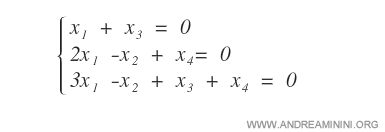
Come prima cosa, trasformo il sistema lineare nella forma matriciale.
La matrice A è la matrice dei coefficienti mentre la matrice A|B è la matrice completa.
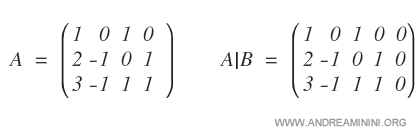
Essendo rettangolare la matrice dei coefficienti (A) non posso usare il teorema di Cramer.
Per trasformarlo in un sistema quadrato utilizzo il metodo di eliminazione di Gauss-Jordan.
Tramite le mosse di Gauss modifico la matrice A|B in una matrice a gradini.

Ora posso calcolare il rango delle matrici A e A|B contando il numero dei pivot.

La matrice completa (A|B) e la matrice dei coefficienti (A) hanno lo stesso rango.
Quindi, secondo il teorema di Rouché-Capelli il sistema lineare ha una o più soluzioni.
A questo punto devo parametrizzare le variabili corrispondenti alle colonne della matrice dei coefficienti prive di pivot.

In questo modo ho trovato le prime due soluzioni assegnando le variabili x1=t1 e x2=t2.
Posso riscrivere il sistema con le modifiche nel seguente modo.

Poi sposto tutte le costanti dalla parte dei termini noti.

Ho così trovato le soluzioni delle altre due variabili del sistema x1 e x2.
Nota. In questo caso le soluzioni sono già calcolate. Tuttavia, non è detto che sia sempre così. In altri casi, per trovare la soluzione di x1 e x2 sarebbe comunque sufficiente applicare il teorema di Cramer, perché ora la matrice dei coefficienti è quadrata.
Considerando anche le variabili già trovate x3 e x4, La soluzione completa del sistema è la seguente:

Ho così calcolato la soluzione del sistema lineare utilizzando il metodo di eliminazione di Gauss Jordan.
