Teorema di struttura delle soluzioni di un sistema lineare
Prendiamo due sistemi lineari.
- ΣB è un sistema lineare non omogeneo AX=B. L'insieme delle soluzioni di ΣB e SB.
- ΣO un sistema lineare omogeneo associato AX=O. L'insieme delle soluzioni di ΣO è SO.
Nota. Nella forma matriciale i due sistemi lineari hanno la stessa matrice dei coefficienti A e lo stesso vettore delle variabili incognite X. Ciò che cambia è il vettore dei termini noti rispettivamente B e O. Nel secondo caso, essendo un sistema omogeneo il vettore dei termini noti è composto da zeri.
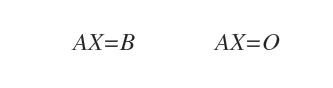
In questo caso ci sono due scenari possibili:
- SB=insieme vuoto.
- SB=SO+X'
(dove X' è un elemento di SB).
Nel secondo caso, la soluzione del sistema SB può essere ottenuta sommando una soluzione X' di ΣB a ogni soluzione del sistema omogeneo ΣO.
Un esempio pratico
Il seguente sistema lineare ha tre equazioni e tre variabili incognite.
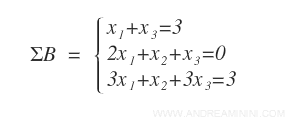
La matrice dei coefficienti A e la matrice completa A|B sono le seguenti:
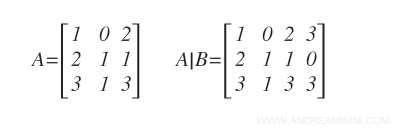
Trasformo la matrice completa A|B in una matrice a gradini utilizzando il metodo di eliminazione di Gauss.
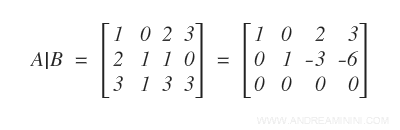
La riduzione in matrice a gradini mi permette di eliminare la terza equazione del sistema perché è nulla e trasformare la variabile x3 in un parametro t del sistema.
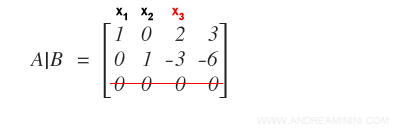
La versione ridotta della matrice completa A|B è la seguente:
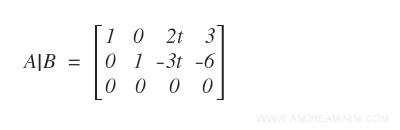
Posso riscrivere il sistema lineare ΣB in questo modo
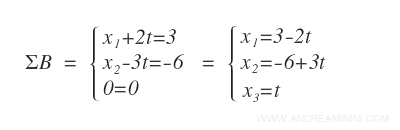
Ho così trovato le soluzioni SB del sistema ΣB
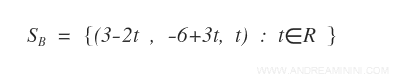
A questo punto, ripeto la stessa procedura per calcolare le soluzioni del sistema omogeneo associato ΣO.
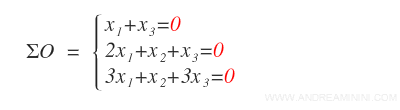
Nella forma matriciale il sistema ΣO equivale al prodotto tra le matrixi AX=O.
La matrice dei coefficienti A e la matrice completa A|B sono le seguenti:
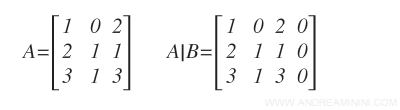
Trasformo la matrice completa A|B in una matrice a gradini tramite il metodo di eliminazione di Gauss.
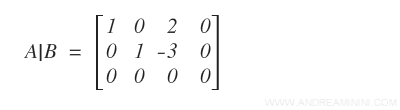
Nella forma a matrice posso eliminare la terza riga ( equazione ) e parametrizzare la variabile x3.
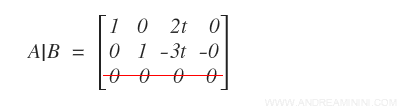
Posso riscrivere il sistema lineare omogeneo ΣO nel seguente modo:
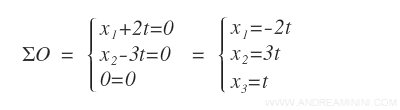
Ho così trovato anche le soluzioni SO del sistema ΣO
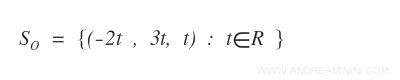
Secondo il teorema di struttura la soluzione SB è uguale alla somma tra la soluzione del sistema omogeneo SO e una soluzione particolare X' di SB.
Quindi la soluzione generale del sistema è

In conclusione, la soluzione SB del sistema ΣB è ottenuta sommando una particolare soluzione X' di SB alla soluzione SO del sistema omogeneo ΣO.
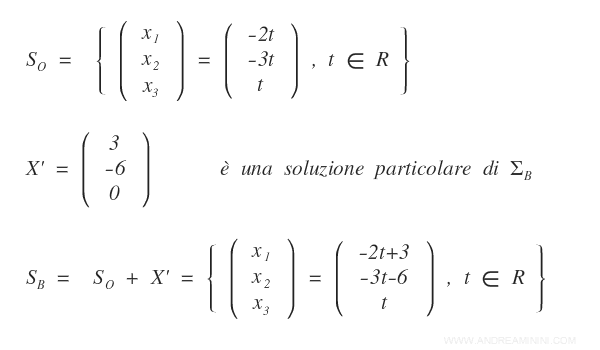
La dimostrazione del teorema di struttura
Una dimostrazione del teorema di struttura dei sistemi lineari è la seguente:

Nota. Se l'insieme delle soluzioni SB è vuoto non c'è nulla da dimostrare perché non esiste X'.
