I sistemi lineari omogenei e i sottospazi vettoriali
L'insieme delle soluzioni di un sistema lineare omogeneo è un sottospazio vettoriale.
Cos'è un sistema lineare?
Un sistema lineare è un sistema di m equazioni, n variabili incognite (x) e n termini noti (b).
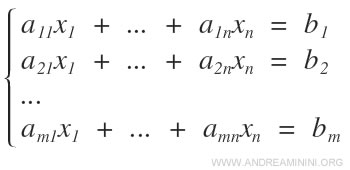
Questo sistema può essere rappresentato anche sotto forma di matrici AX=B.
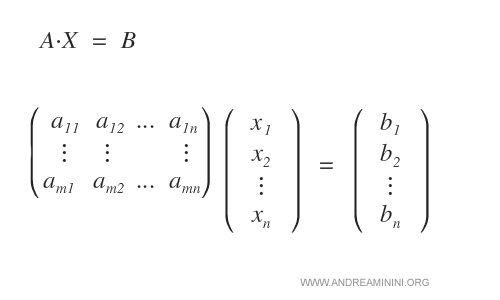
Dove A è la matrice m x n dei coefficienti delle equazioni, X è la matrice colonna n x 1 ( vettore ) delle incognite x1,...,xn e B è la matrice colonna n x 1 dei termini noti.
Il sistema lineare è detto omogeneo se tutti i termini noti delle equazioni sono uguali a zero.
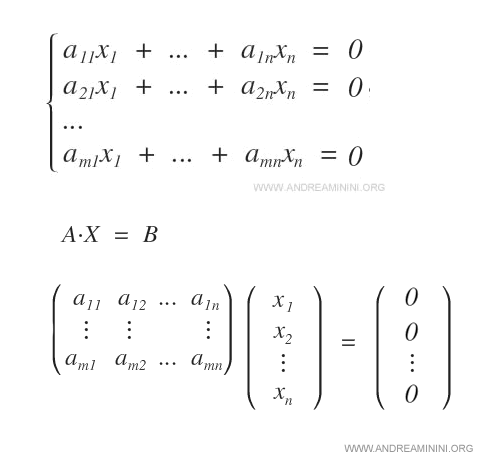
Perché le soluzioni del sistema omogeneo sono un sottospazio vettoriale
L'insieme delle soluzioni X del sistema lineare omogeneo è un sottoinsieme dell'insieme dei numeri reali R.
\(X \in R \)
L'insieme delle soluzioni X è anche un sottospazio vettoriale di Rn.
\(X \in R^n \)
La dimostrazione
Per dimostrare questa affermazione parto dalle due proprietà dei sottospazi vettoriali.
Prima proprietà ( chiusura rispetto ala somma )
Dati due elementi qualsiasi (w1+w2) del sottoinsieme W, anche la loro somma appartiene a W.
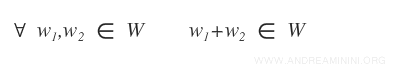
Nel caso del sistema lineare il sottoinsieme da verificare è X.
Prendo due elementi generici X1 e X2 di X.
Li sommo X1+X2 e verifico se la somma appartiene all'insieme X.
\(A(X_1 + X_2 = 0 ) \)
\(AX_1 + AX_2 = 0 \)
Un sistema omogeneo ha sempre una soluzione banale ossia un vettore X composto soltanto da zeri { 0, ... , 0 }.
Sostituisco lo zero agli elementi generici X1 e X2.
\(A(0) + A(0) = 0 \)
L'equazione è verificata.
La somma A(X1+X2) appartiene all'insieme X.
\(A(X_1 + X_2) \in X \)
L'insieme X è chiuso rispetto all'addizione.
Quindi la prima proprietà dei sottospazi è stata soddisfatta.
Seconda proprietà ( chiusura rispetto al prodotto scalare )
Dato uno scalare generico λ del campo K e un elemento qualsiasi (w1) dell'insieme W, il loro prodotto scalare λw1appartiene a W.
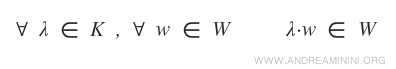
Nel caso del sistema lineare il sottoinsieme da verificare è X e il campo K è l'insieme dei numeri reali R.
Prendo un elemento generico X1 di X e uno scalare generico λ di R.
Li moltiplico λX1 e verifico se il prodotto scalare appartiene all'insieme X.
\(λ(X_1) = 0 \)
Anche in questo caso prendo la soluzione banale dell'insieme omogeneo, ossia lo zero, e lo sostituisco a X1.
\(λ(0) = 0 \)
Qualunque sia il valore λ , l'equazione è verificata.
Il prodotto scalare λ(X1) appartiene all'insieme X.
\(λ(X_1) \in X \)
L'insieme X è chiuso rispetto al prodotto scalare.
Quindi anche la seconda proprietà dei sottospazi è stata soddisfatta.
Il sottoinsieme delle soluzioni X soddisfa entrambe le proprietà dei sottospazi vettoriali. E' chiuso sia alla somma che al prodotto scalare. Pertanto, l'insieme X è un sottospazio vettoriale di Rn.
Il caso dei sistemi lineari non omogenei
Un sistema lineare non omogeneo non è uno spazio vettoriale di Rn.
Non avendo una soluzione banale, il suo sottoinsieme delle soluzioni X non soddisfa le due proprietà dei sottospazi vettoriali.
