Il metodo di Cramer per sistemi rettangolari
Uno dei limiti del teorema di Cramer è l'applicazione ai soli sistemi lineari quadrati. Questo riduce drasticamente l'applicabilità del metodo. Tuttavia, c'è una soluzione.
Se il sistema rettangolare può essere trasformato in un sistema quadrato, è possibile usare il metodo di Cramer per trovare le soluzioni.
Ad esempio, è possibile usare il metodo di Cramer in una matrice 3x4 se può essere trasformata in una matrice 3x3 o 2x2.
Come ridurre un sistema rettangolare in sistema quadrato
Per trasformare un sistema rettangolare in un sistema quadrato, bisogna eliminare le equazioni ridondanti ed individuare i parametri che determinano le soluzioni del sistema.
Il metodo di riduzione
- Data la matrice M corrispondente a un minore non nullo di ordine massimo che determina il rango r della matrice dei coefficienti A e della matrice A|B:
- possono essere eliminate le equazioni corrispondenti alle righe di A non presenti in M.
- possono essere scelte come parametri le incognite corrispondenti alle colonne di A non presenti in M.
Un esempio pratico
Il seguente sistema lineare rettangolare è composto da tre equazioni e quattro variabili incognite.
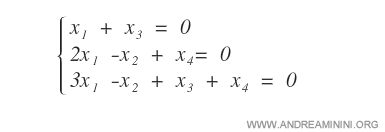
Come prima cosa, trasformo il sistema in forma matriciale.
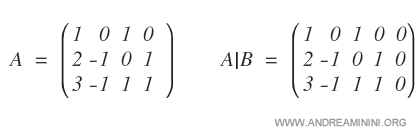
Non si può utilizzare il metodo di Cramer per la risoluzione perché la matrice dei coefficienti A non è quadrata. E' una matrice 3x4.
Come trasformarla in una matrice quadrata?
Prima di procedere devo assicurarmi che il sistema abbia delle soluzioni.
Calcolo il minore della matrice dei coefficienti e della matrice completa per calcolarne il rango.
Poi seleziono le ultime due righe e la terza e quarta colonna per estrarre una sottomatrice A(2,3)(3,4).
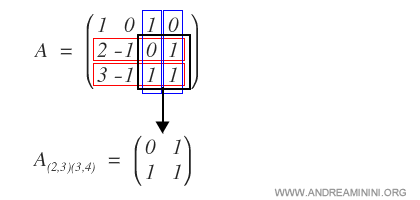
Ora calcolo il determinante della sottomatrice ossia il minore.
Il minore di A(2,3)(3,4) è diverso da zero, quindi il rango della matrice A è uguale o maggiore di 2.
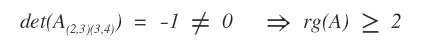
Per verificare se la matrice ha rango superiore a due utilizzo il teorema degli orlati sul minore A(2,3)(3,4).
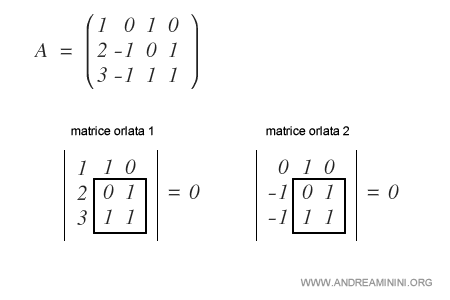
Non esistendo una matrice orlata di ordine tre con determinante diverso da zero, si deduce che la matrice non ha rango tre.
Quindi il rango della matrice A è uguale a 2.
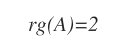
A questo punto devo calcolare anche il rango della matrice completa A|B.
Essendo tutti i termini noti uguali a zero, evito di fare i calcoli perché si deduce che anche il rango della matrice A|B è uguale a 2.
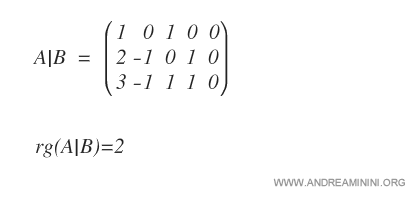
Secondo il teorema di Rouché-Capelli, il sistema ha una o più soluzioni perché il rango di A è uguale al rango di A|B.
In particolar modo, essendoci quattro variabili incognite (n=4) e il rango uguale a due (r=2), il sistema ha infinite soluzioni.
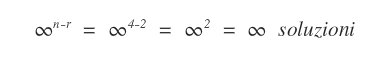
Una volta assodato che il sistema ammette delle soluzioni, posso provare a ridurre la matrice dei coefficienti A in una matrice quadrata equivalente.
1] Elimino la prima riga della matrice perché non influenza le soluzioni del sistema.
La prima equazione del sistema corrispondente alla prima riga della matrice A può essere eliminata perché non è presente nel minore di ordine massimo A(2,3)(3,4).
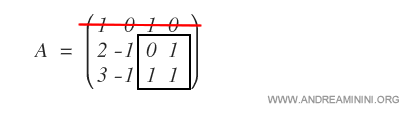
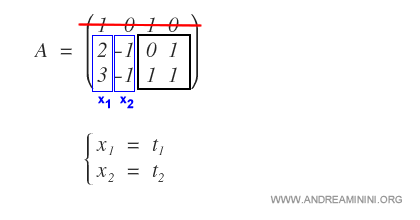
2] Alle prime due colonne assegno dei parametri t1 e t2.
Le prime due colonne corrispondono alle incognite x1 e x2. Non essendo presenti nel minore possono essere parametrizzate.
Queste modifiche consentono di riscrivere il sistema di equazioni nel seguente modo:
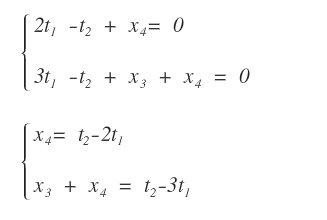
In questa forma parametrizzata il sistema lineare ha una matrice dei coefficienti quadrata (A).
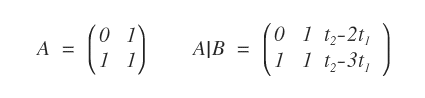
E' quindi possibile usare il teorema di Cramer per trovare le soluzioni del sistema.
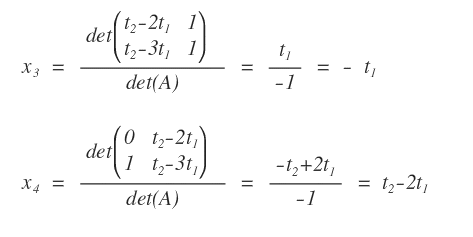
In questo modo ho trovato anche le soluzioni per le incognite x3 e x4.
Nota. Le soluzioni delle incognite x1 e x2 non vanno calcolate perché sono state già parametrizzate in precedenza.
Quindi posso scrivere la soluzione completa del sistema lineare.
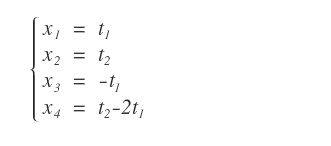
In conclusione, grazie a questo procedimento ho potuto usare il teorema di Cramer per trovare le soluzioni di un sistema lineare rettangolare.
Attenzione. La scelta dei parametri dipende dal minore preso inizialmente come riferimento. Indirettamente, dai parametri dipende la rappresentazione formale delle soluzioni del sistema. Quindi, la risoluzione non dipende da una scelta oggettiva e univoca, bensì soggettiva. Alcune scelte sono più corrette di altre.
