L'equazione lineare
Un'equazione è detta lineare se può essere espressa come un polinomio di grado 1 uguagliato a 0.
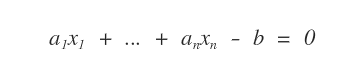
La definizione di equazione lineare
Se p(x1, ..., xn ) è un polinomio di grado 1 con n incognite x1, ...,xn
a1x1 + ... + anxn -b
dove n appartiene all'insieme dei numeri interi Z ed è maggiore e uguale a 1
n ∈ Z ≥ 1
e sia i coefficienti a1,...,an che il termine noto b sono numeri reali,
allora
a1x1 + ... + anxn -b = 0
è un'equazione lineare a n incognite
Nota. Il caso più semplice è un'equazione lineare con una incognita a1x1 -b = 0 o più semplicemente a1x1 = b.
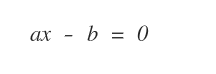
La soluzione dell'equazione lineare
Data un'equazione lineare a n incognite
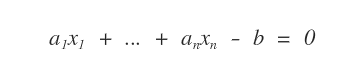
la soluzione è una n-pla ordinata di numeri reali ( s1,..., sn )
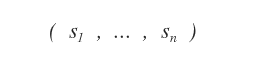
che sostituiti ordinatamente alle incognite ( x1, ..., xn ) rendono vera l'equazione.
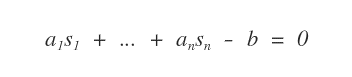
Esempi di equazioni lineari
Le seguenti equazioni sono esempi di equazioni lineari.
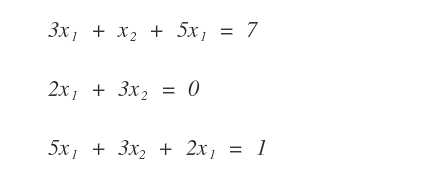
E le equazioni non lineari come si riconoscono?
Un'equazione algebrica polinomiale potrebbe non essere lineare per diversi motivi.
- se il polinomio è di grado superiore al primo
- se l'equazione non è polinomiale ( ad esempio se è trascendente )
Esempi di equazioni non lineari:
La rappresentazione geometrica
Un'equazione lineare è rappresentata in uno spazio di dimensione N, pari al numero delle incognite.
Esempio di equazione lineare a due incognite
La sequente equazione lineare ha due variabili incognite (x1,x2)
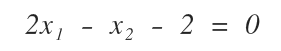
e può essere rappresentata graficamente tramite una retta sul piano cartesiano.
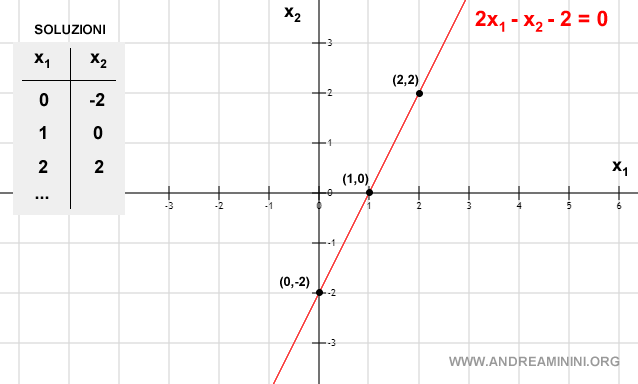
Le coordinate (x1,x2) dei punti della retta sul piano identificano le coppie ordinate di numeri reali delle soluzioni possibili dell'equazione lineare.
Le soluzioni dell'equazione lineare sono infinite
L'insieme delle soluzioni possibili dell'equazione lineare è infinito così come i punti della retta.
