Equazione segmentaria del piano
L'equazione segmentaria del piano si ottiene trovando dei coefficienti p, q, r tali da rendere l'equazione cartesiana del piano uguale a $$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
L'equazione cartesiana del piano è
$$ ax+by+cz+d=0 $$
Ponendo y e z a zero ottengo
$$ ax+d=0 \\ ax=-d \\ x=-\frac{d}{a} $$
Ponendo x e z a zero ottengo
$$ by+d=0 \\ by=-d \\ y=-\frac{d}{b} $$
Ponendo x e y a zero ottengo
$$ cz+d=0 \\ cz=-d \\ z=-\frac{d}{c} $$
Assegno i rapporti appena trovati ai coefficienti p, q, e r
$$ p = -\frac{d}{a} $$
$$ q = -\frac{d}{b} $$
$$ r =-\frac{d}{c} $$
Ho così trovato l'equazione segmentaria del piano
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
A cosa serve l'equazione segmentaria della retta?
I punti p, q, r sono i punti di intersezione del piano con gli assi.
- p = intersezione asse x
- q = intersezione asse y
- r = intersezione asse q
Un esempio pratico
Un piano è definito da questa equazione cartesiana
$$ -5x-y+8z+15=0 $$
Metto y e z a zero (y=z=0) per ottenere il punto di intersezione sull'asse x.
$$ -5x+15=0 \\ x=\frac{15}{5} \\ x=3 $$
Metto x e z a zero (x=z=0) per ottenere il punto di intersezione sull'asse y.
$$ -y+15=0 \\ -y=-15 \\ y=15 $$
Metto x e y a zero (x=y=0) per ottenere il punto di intersezione sull'asse z.
$$ 8z+15=0 \\ 8z=-15 \\ z=-\frac{15}{8} $$
Ho così trovato i coefficienti p, q, r dell'equazione segmentaria.
$$ p=3 $$
$$ q=15 $$
$$ r=-\frac{15}{8} $$
Quindi l'equazione segmentaria del piano è
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
$$ \frac{x}{3} + \frac{y}{15} + \frac{z}{-\frac{15}{8}} = 1 $$
In questa forma i coefficienti dell'equazione cartesiana sono i punti di intersezione del piano con gli assi cartesiani (x,y,z).
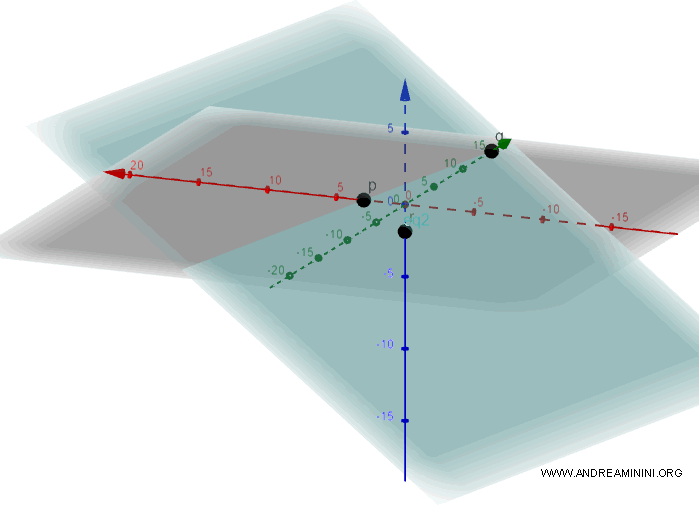
Nota. La rappresentazione grafica del piano e dei punti di intersezione p, q, r.