L'equazione del piano per tre punti non allineati

Dati tre punti non allineati nello spazio R³, per i tre punti P₁, P₂ e P₃ passa un unico piano. $$ P_1 \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} $$

Come determinare le equazioni parametriche del piano

Dati tre punti $ P_1(x_1,y_1,z_1) $, $ P_2(x_2,y_2,z_2) $, $ P_3(x_3,y_3,z_3) $, se il piano non è parallelo all'asse z, posso utilizzare l'equazione esplicita del piano

$$ z = mx + ny + q $$

Sostituendo le coordinate dei tre punti, ottengo un sistema di tre equazioni.

$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$

La soluzione del sistema mi permette di i valori delle incognite m, n, q e così individuare l'equazione del piano.

Nota. Questo metodo è corretto, a patto che il piano ammetta la forma esplicita, cioè che non sia verticale (parallelo all’asse $ z $).

Come capire se il sistema è risolvibile?

Per capire se il sistema è risolvibile, cioè se i tre punti determinano un piano che può essere scritto nella forma esplicita $ z = mx + ny + q $, trasformo il sistema di equazioni in forma matriciale:

$$
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
m \\
n \\
q
\end{bmatrix}
=
\begin{bmatrix}
z_1 \\
z_2 \\
z_3
\end{bmatrix}
$$

Dove $ A $ è la matrice dei coefficienti:

$$
A =
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
$$

Il sistema ha una soluzione unica se la matrice $ A $ ha determinante diverso da zero:

$\det(A) \ne 0$

Se $ \det(A) \ne 0 $, allora il piano non è parallelo all'asse $ z $, posso risolvere il sistema e scrivere il piano in forma esplicita.

Viceversa, se $ \det(A) = 0 $, allora il piano è verticale, non posso usare la forma esplicita, ma posso comunque trovare la forma implicita $ ax + by + cz + d = 0 $ con un altro metodo.

Che significato geometrico ha $ \det(A) = 0 $? Se il determinante è zero, significa che le proiezioni dei tre punti sul piano $ xy $ sono allineate, cioè i punti proiettati $ (x_i,y_i) $ sono su una retta.  In questo caso il piano risulta "verticale", e non è possibile scriverlo nella forma $ z = mx + ny + q $.

Esempio

Considero tre punti non allineati dello spazio

$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$

Costruisco il sistema di equazioni con le coordinate dei punti

$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$

$$ \begin{cases} m(1) + n(3) + q = 5 \\ m(2) + n(0) + q = 3 \\ m(4) + n(1) + q =2 \end{cases} $$

$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q =2 \end{cases} $$

La matrice dei coefficiente $ A $ del sistema è:

$$
A =
\begin{bmatrix}
1 & 3 & 1 \\
2 & 0 & 1 \\
4 & 1 & 1
\end{bmatrix}
$$

Calcolo il determinante della matrice

$$ \Delta = (1 \cdot 0 \cdot 1)+( 3 \cdot 1 \cdot 4) + (1 \cdot 2 \cdot 1) - (1 \cdot 0 \cdot 4) - (3 \cdot 2 \cdot 1) - (1 \cdot 1 \cdot 1) $$

$$ \Delta = 0+12+ 2 -0 -6- 1 = 7 $$

Il determinante $ \Delta = 7 $ è diverso da zero, quindi il sistema di equazioni ha una soluzione.

$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q =2 \end{cases} $$

Per risolvere il sistema utilizzo il metodo di Cramer.

Sostituisco la prima colonna con il termine noto $ (5,3,2) $:

$$ \Delta_m = \begin{vmatrix} 5 & 3 & 1 \\ 3 & 0 & 1 \\ 2 & 1 & 1 \end{vmatrix} $$

$$ \Delta_m = 5 \cdot \begin{vmatrix} 0 & 1 \\ 1 & 1 \end{vmatrix} - 3 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix}
+ 1 \cdot \begin{vmatrix} 3 & 0 \\ 2 & 1 \end{vmatrix} $$

$$ \Delta_m = 5(-1) - 3(1) + 1(3) = -5 - 3 + 3  $$

$$ \Delta_m = -5 $$

Sostituisco la seconda colonna con il termine noto:

$$ \Delta_n = \begin{vmatrix} 1 & 5 & 1 \\ 2 & 3 & 1 \\ 4 & 2 & 1 \end{vmatrix} $$

$$ \Delta_n = 1 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} - 5 \cdot \begin{vmatrix} 2 & 1 \\ 4 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} $$

$$ \Delta_n = 1(1) - 5(-2) + 1(-8) = 1 + 10 - 8  $$

$$ \Delta_n = 3 $$

Sostituisco la terza colonna:

$$ \Delta_q = \begin{vmatrix} 1 & 3 & 5 \\ 2 & 0 & 3 \\ 4 & 1 & 2 \end{vmatrix} $$

$$ \Delta_q = 1 \cdot \begin{vmatrix} 0 & 3 \\ 1 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 2 & 0 \\ 4 & 1 \end{vmatrix} $$

$$ \Delta_q = 1(-3) - 3(-8) + 5(2) = -3 + 24 + 10  $$

$$ \Delta_q = 31 $$

Ora applico Cramer:

$$ m = \frac{\Delta_m}{\Delta} = \frac{-5}{7} $$

$$ n = \frac{\Delta_n}{\Delta} = \frac{3}{7} $$

$$ q = \frac{\Delta_q}{\Delta} = \frac{31}{7} $$

Quindi, il risultato finale è

$$ \begin{cases} m = -\frac{5}{7} \\ n = \frac{3}{7} \\ q = \frac{31}{7} \end{cases}  $$

Sostituisco $ m $, $ n $ e $ q $ nell'equazione esplicita del piano $ mx + ny + q = z $

$$ -\frac{5}{7} x + \frac{3}{7}y +  \frac{31}{7} = z $$

Questa è l'equazione del piano che passa per i punti $ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $

Metodo alternativo e generale

Questo metodo alternativo mi permette di  trovare l’equazione del piano nella forma generale (o implicita) dati tre punti:

$a x + b y + c z + d = 0$

Ha il vantaggio di funzionare sempre, anche se il piano è verticale o orizzontale. Inoltre, non richiede di risolvere un sistema.

Tuttavia, è un po' più complesso perché richiede la conoscenza del calcolo vettoriale.

Come funziona?

Inizialmente conosco le coordinate di tre punti nello spazio

$$
P_1(x_1,y_1,z_1), \quad
P_2(x_2,y_2,z_2), \quad
P_3(x_3,y_3,z_3)
$$

Prendo due vettori diretti nel piano:

$$ \vec{v_1} = P_2 - P_1 = (x_2 - x_1, \ y_2 - y_1, \ z_2 - z_1) $$

$$ \vec{v_2} = P_3 - P_1 = (x_3 - x_1, \ y_3 - y_1, \ z_3 - z_1) $$

Calcolo il prodotto vettoriale $ \vec{n} = \vec{v_1} \times \vec{v_2} $ che mi restituisce un vettore normale al piano:

$$
\vec{n} = (a, b, c) =
\left|
\begin{matrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\
x_3 - x_1 & y_3 - y_1 & z_3 - z_1
\end{matrix}
\right|
$$

Le componenti del vettore normale sono i coefficienti $ a $, $ b $ e $ c $ dell'equazione generale del piano.

In modo più diretto, posso anche calcolare i coefficienti dell'equazione del piano usando queste formule:

$$ a = (y_2 - y_1)(z_3 - z_1) - (y_3 - y_1)(z_2 - z_1) $$

$$ b = (z_2 - z_1)(x_3 - x_1) - (z_3 - z_1)(x_2 - x_1) $$

$$ c = (x_2 - x_1)(y_3 - y_1) - (x_3 - x_1)(y_2 - y_1) $$

Ora che ho $ a, b, c $, scrivo l'equazione del piano in forma generale (implicita) usando le coordinate di un punto

$$ a (x - x_1) + b (y - y_1) + c (z - z_1) = 0 $$

In alternativa, posso scrivere l'equazione in forma implicita

$$ a x + b y + c z + d = 0 $$

Dove il termine noto $ d $ è:

$$ d = - (a x_1 + b y_1 + c z_1) $$

In entrambi i casi il risultato finale è l'equazione generale del piano.

Se $ c \ne 0 $, allora posso isolare $ z $ e scrivere anche l'equazione in forma esplicita.

$$ z=− \frac{a}{c} x− \frac{b}{c}y− \frac{d}{c} $$

Ma ovviamente non sempre è possibile farlo, perché se $ c = 0 $ il piano è verticale rispetto a $ z $.

Esempio

Considero gli stessi tre punti dell'esempio precedente

$$
P_1 = (1, 3, 5), \quad
P_2 = (2, 0, 3), \quad
P_3 = (4, 1, 2)
$$

Calcolo i vettori del piano

$$ \vec{v_1} = P_2 - P_1 = (2 - 1, \ 0 - 3, \ 3 - 5) = (1, \ -3, \ -2) $$

$$ \vec{v_2} = P_3 - P_1 = (4 - 1, \ 1 - 3, \ 2 - 5) = (3, \ -2, \ -3) $$

Calcolo il prodotto vettoriale tra i due vettori

$$ \vec{n} = \vec{v_1} \times \vec{v_2} = (a, b, c) $$

Per calcolarlo uso la formula del determinante:

$$ \vec{n} =  \left| \begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & -3 & -2 \\ 3 & -2 & -3  \end{matrix} \right| $$

$$\vec{n} = \mathbf{i} \cdot \left| \begin{matrix}-3 & -2 \\-2 & -3 \end{matrix}\right| - \mathbf{j} \cdot \left| \begin{matrix}1 & -2 \\3 & -3 \end{matrix}\right|+\mathbf{k} \cdot \left| \begin{matrix}1 & -3 \\3 & -2 \end{matrix}\right|$$

$$\vec{n} = \mathbf{i} \cdot [ (-3)(-3) - (-2)(-2)  ]  - \mathbf{j} \cdot [  (1)(-3) - (3)(-2)  ] + \mathbf{k} \cdot [ (1)(−2)−(3)(−3) ] $$

$$\vec{n} = \mathbf{i} \cdot ( 9 - 4 ) - \mathbf{j} \cdot (  -3 + 6  ) +\mathbf{k} \cdot  (  -2 - (-9) ) $$

$$\vec{n} = \mathbf{i} \cdot 5  - \mathbf{j} \cdot (-3) +\mathbf{k} \cdot 7 $$

$$\vec{n} = 5 \mathbf{i} + 3 \mathbf{j} + 7 \mathbf{k}  $$

Quindi, il vettore normale finale è $ \vec{n} = (5, -3, 7) $

La componente $ a $ è il coefficiente di $ \mathbf{i} $.

$$ a= 5 $$

La componente $ b $ è il coefficiente di $ \mathbf{j} $.

$$ b= 3 $$

La componente $ c $ è il coefficiente di $ \mathbf{k} $.

$$ c=7 $$

Una volta trovati i coefficienti $ a $, $ b $, $ c $ posso scrivere l’equazione del piano:

$$ 5(x - 1) -3(y - 3) + 7(z - 5) = 0 $$

Svolgo i calcoli algebrici

$$ 5x - 5 - 3y + 9 + 7z - 35 = 0 $$

$$ 5x - 3y + 7z - (5 - 9 + 35) = 0 $$

$$ 5x - 3y + 7z - 31 = 0 $$

Quindi, l'equazione generale del piano è

$$5x - 3y + 7z = 31 $$

Poiché il coefficiente di $ z $ è diverso da zero, posso scrivere anche l'equazione del piano in forma implicita, con un semplice passaggio algebrico.

Ricavo $ z $

$$  7z = - 5x + 3y+ 31 $$

Poi divido entrambi i membri dell'equazione per 7.

$$  \frac{ 7z }{ 7 } = \frac{ - 5x + 3y+ 31 }{ 7} $$

In questo modo ottengo l'equazione implicita del piano che passa per i tre punti.

$$ z = -\frac{5}{7} x + \frac{3}{7}y +  \frac{31}{7}  $$

E' lo stesso risultato che ho ottenuto con il metodo precedente.

Il metodo vettoriale

Dai i tre punti ottengo due vettori direttori:

$$ v_1 = P_1P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} $$

$$ v_2 = P_1P_3 = \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$

A questo punto verifico che siano linearmente indipendenti.

I due vettori possono generare il piano, ossia formano un generatore dello spazio vettoriale, soltanto se sono vettori linearmente indipendenti.

Due vettori sono linearmente indipendenti se il rango della matrice costruita con i due vettori in colonna è uguale al numero dei vettori.

$$ r_k \begin{pmatrix} x_2 - x_1 & x_3 - x_1 \\ y_2 - y_1 & y_3 - y_1 \\ z_2 - z_1 & z_2 - z_1 \end{pmatrix} = 2 $$

Una volta appurato l'indipendenza lineare dei due vettori, scelgo uno dei tre punti come punto P₀ qualsiasi del piano.

Ad esempio, scelgo il punto P₁.

$$ P_0 = P_1 $$

$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $$

A questo punto ho tutti gli elementi per scrivere l'equazione vettoriale del piano.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot v_1 + t_2 \cdot v_2 $$

Dove t₁ e t₂ sono i parametri dell'equazione vettoriale che determinano tutti i punti del piano.

Sostituisco i due vettori direttori.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$

Poi sostituisco il punto P₀

Ho così ottenuto l'equazione vettoriale del piano.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$

Per ottenere l'equazione parametrica del piano, mi basta trasformare la forma vettoriale in un sistema di tre equazioni.

$$ \begin{cases} x = x_0 + t_1 \cdot ( x_2 - x_1 ) + t_2 \cdot ( x_3 - x_1 ) \\ y = y_0 + t_1 \cdot ( y_2 - y_1 ) + t_2 \cdot ( y_3 - y_1 ) \\ z = z_0 + t_1 \cdot ( z_2 - z_1 ) + t_2 \cdot ( z_3 - z_1 ) \end{cases} $$

Per calcolare l'equazione cartesiana risolvo l'equazione parametrica.

Sposto il punto P₀ nel membro di sinistra.

$$ \begin{cases} x - x_0 = t_1 \cdot ( x_2 - x_1 ) + t_2 \cdot ( x_3 - x_1 ) \\ y - y_0 = t_1 \cdot ( y_2 - y_1 ) + t_2 \cdot ( y_3 - y_1 ) \\ z - z_0 = t_1 \cdot ( z_2 - z_1 ) + t_2 \cdot ( z_3 - z_1 ) \end{cases} $$

Poi costruisco la matrice con i coefficienti dei tre vettori in colonna

$$ \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} $$

Infine calcolo il determinante della matrice e lo metto uguale a zero.

$$ det \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} = 0 $$

$$ ( x-x_0 ) \cdot \begin{vmatrix} y_2-y_1 & y_3 - y_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} - (y-y_0) \cdot \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} +(z-z_0) \cdot \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ y_2-y_1 & y_3 - y_1 \end{vmatrix} = 0$$

Ho così ottenuto l'equazione cartesiana del piano.

$$ ( x-x_0 ) \cdot a - (y-y_0) \cdot b +(z-z_0) \cdot c = 0$$

Esempio

Ho tre punti non allineati dello spazio

$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$

Con i punti ottengo dei vettori direttori

$$ v_1 = P_1P_2 = \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 2 - 1 \\ 0 - 3 \\ 3 - 5 \end{pmatrix} = \begin{pmatrix} 1 \\ - 3 \\ -2 \end{pmatrix} $$

$$ v_2 = P_1P_3 = \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 4 - 1 \\ 1 - 3 \\ 2 - 5 \end{pmatrix} = \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$

Verifico che siano linearmente indipendenti

$$ r_k \begin{pmatrix} 1 & 3 \\ -3 & -2 \\ -2 & -3 \end{pmatrix} = 2 $$

Il rango (r_k=2) è uguale al numero dei vettori (2).

Quindi i vettori sono linearmente indipendenti e posso usarli come vettori del generatore del piano.

Scelgo il punto P₁ come punto P₀ qualsiasi del piano.

$$ P_0 = P_1 $$

$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} $$

Ho tutti gli elementi per scrivere l'equazione vettoriale del piano.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot v_1 + t_2 \cdot v_2 $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 1 \\ - 3 \\ -2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$

E da quest'ultima ottengo l'equazione parametrica del piano.

$$ \begin{cases} x = 1 + t_1 \cdot 1 + t_2 \cdot 3 \\ y = 3 + t_1 \cdot (-3) + t_2 \cdot (-2) \\ z = 5 + t_1 \cdot (-2) + t_2 \cdot (-3) \end{cases} $$

$$ \begin{cases} x = 1 + t_1 + 3 t_2 \\ y = 3 - 3 t_1 -2 t_2 \\ z = 5 - 2 t_1 -3 t_2 \end{cases} $$

Infine, ottengo l'equazione cartesiana del piano calcolando il determinante della matrice.

Sposto le coordinate del punto P₀ nel membro di sinistra

$$ \begin{cases} x - 1 = t_1 + 3 t_2 \\ y - 3 = - 3 t_1 -2 t_2 \\ z - 5 = - 2 t_1 -3 t_2 \end{cases} $$

Trasformo il sistema in una matrice

$$ \begin{pmatrix} x - 1 & 1 & 3 \\ y-3 & -3 & -2 \\ z-5 & -2 & -3 \end{pmatrix} $$

Calcolo il determinante della matrice

$$ det \begin{pmatrix} x - 1 & 1 & 3 \\ y-3 & -3 & -2 \\ z-5 & -2 & -3 \end{pmatrix} $$

$$ ( x-1 ) \cdot \begin{vmatrix} -3 & -2 \\ -2 & -3 \end{vmatrix} - (y-3) \cdot \begin{vmatrix} 1 & 3 \\ -2 & -3 \end{vmatrix} +(z-5) \cdot \begin{vmatrix} 1 & 3 \\ -3 & -2 \end{vmatrix} $$

$$ ( x-1 ) \cdot (5) - (y-3) \cdot (3) +(z-5) \cdot (7) $$

$$ 5x - 5 -3y +9 +7z -35 $$

$$ 5x -3y +7z -31 $$

Metto a zero l'equazione e ottengo l'equazione cartesiana del piano

$$ 5x -3y +7z -31 = 0 $$

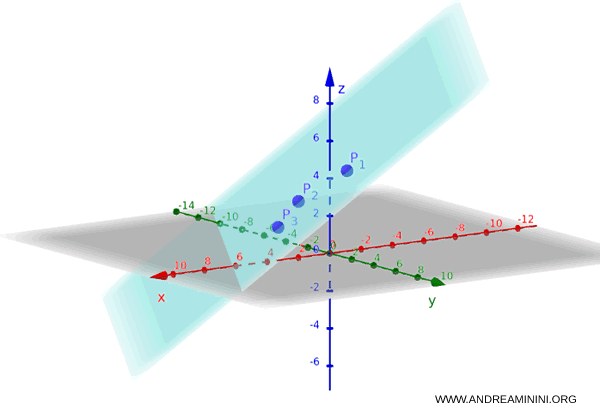
La rappresentazione grafica del piano nello spazio a tre dimensioni è la seguente:

 

 

E così via.