Teorema dell'equivalenza fra un parallelogramma e un triangolo
Un triangolo è equivalente a un parallelogramma che ha la stessa altezza e la metà della base del triangolo.
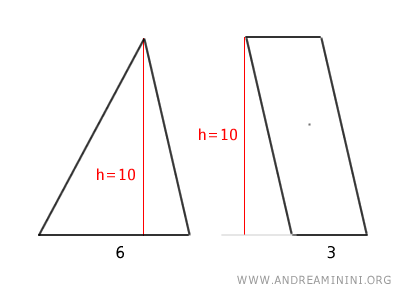
In alternativa, un triangolo è equivalente a un parallelogramma che ha la stessa base e la metà dell'altezza del triangolo.
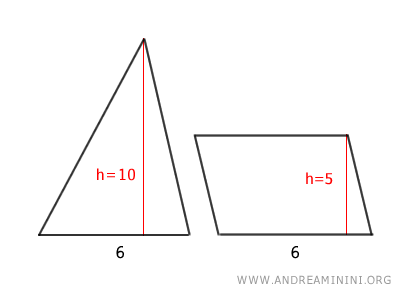
In altre parole, se il triangolo ha la stessa altezza e una base doppia rispetto a quella del parallelogramma, l'area è uguale.
Lo stesso accade quando il triangolo ha la stessa base e un'altezza doppia rispetto al parallelogramma.
Un esempio pratico
Considero un triangolo e un parallelogramma

Il triangolo e il parallelogramma hanno la stessa altezza h=10.
Inoltre, la base del triangolo è 6 ed è esattamente il doppio della base del parallelogramma (3).
Quindi, secondo il teorema dell'equivalenza hanno la superficie equivalente ossia la stessa area.
$$ A_p = A_t $$
Dove Ap e At sono rispettivamente l'area del parallelogramma e del triangolo.
L'area del parallelogramma Ap si calcola moltiplicando la base (3) per l'altezza (10).
$$ A_p = 3 \cdot 10 = 30 $$
Di conseguenza, anche l'area del triangolo At è 30.
$$ A_t = 30 $$
Per verificarlo provo a calcolare l'area del triangolo che, in questo caso, si calcola tramite il prodotto base (6) per altezza (10) diviso due.
$$ A_t = \frac{6 \cdot 10}{2} = \frac{60}{2} = 30 $$
Il risultato è lo stesso.
Esempio 2
In questo caso il parallelogramma ha la stessa base del triangolo (b=6) e metà altezza (hp=5) del triangolo (ht=10)

Secondo il teorema dell'equivalenza, i due poligoni sono equivalenti perché hanno la stessa area.
$$ A_p = A_t $$
Dove Ap e At sono l'area del parallelogramma e del triangolo.
L'area del parallelogramma Ap è il prodotto dela base (6) per l'altezza (5).
$$ A_p = 6 \cdot 5 = 30 $$
Pertanto, anche l'area del triangolo At è 30.
$$ A_t = 30 $$
Il risultato è verificabile facilmente. Basta calcolare l'area del triangolo sapendo che è il semiprodotto della base (6) per l'altezza (10) del triangolo.
$$ A_t = \frac{6 \cdot 10}{2} = \frac{60}{2} = 30 $$
Il risultato è sempre lo stesso.
La dimostrazione
A] Parallelogramma con stessa altezza e metà base del triangolo
Per dimostrare il teorema prendo come esempio un triangolo ABC e un parallelogramma DEFG.
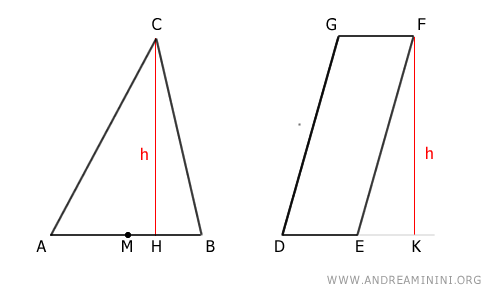
Dove M è il punto medio del segmento AB.
$$ \overline{AM} \cong \overline{BM} $$
Per ipotesi iniziale l'altezza delle due figure geometriche è congruente
$$ \overline{CH} \cong \overline{FK} $$
La relativa base dell'altezza del parallelogramma è congruente alla metà della base del triangolo.
In altre parole la base del triangolo (AB) è il doppio della base del parallelogramma (DE).
$$ \overline{AB} \cong 2 \cdot \overline{DE} $$
ovvero
$$ \overline{AM} \cong \overline{BM} \cong \overline{DE} $$
Devo dimostrare che le due figure ABC e DEFG sono equivalenti ovvero che hanno la stessa area.
Traccio la retta parallela al lato AC del triangolo che passa per il suo punto medio.
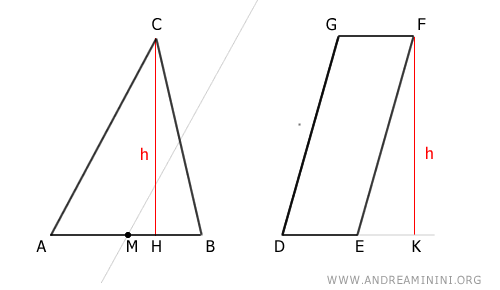
Poi traccio la retta parallela al lato AB del triangolo che passa per il vertice C.
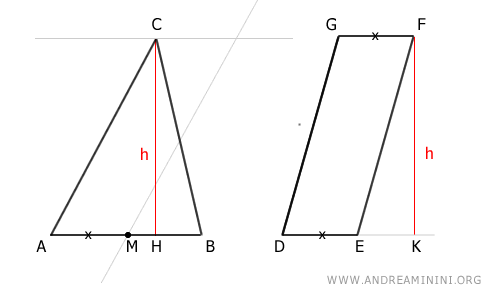
In questo modo ottengo un altro parallelogramma AMNC.
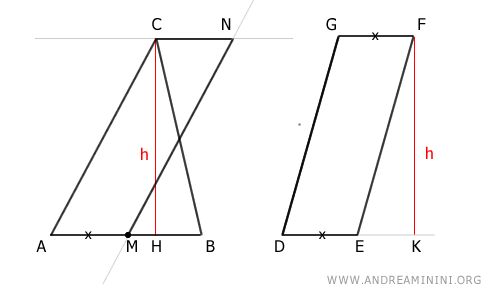
Secondo il teorema dell'equivalenza dei parallelogrammi, il parallelogramma AMNC è equivalente al parallelogramma DEFG perché ha la base (AM≅DE) e l'altezza (CM≅FK) congruente.
$$ AMNC \cong DEFG $$
Ora gli angoli α≅δ e β≅γ sono congruenti perché sono angoli alterni interni di una trasversale tra due rette parallele (teorema delle rette parallele).
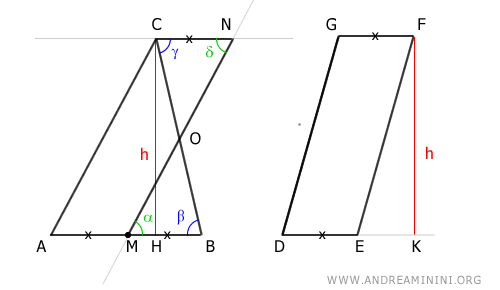
Sapendo anche che BM≅AM perché M è un punto medio e che i lati opposti di un parallelogramma sono paralleli, deduco che anche i lati BM≅CN sono congruenti.
Quindi, i triangoli MBO e CNO sono congruenti per il secondo criterio di congruenza dei triangoli, in quanto hanno un lato congruente BM≅CN e gli angoli adiacenti congruenti α≅δ e β≅γ.
$$ MBO \cong CNO $$
Essendo congruenti, i due triangoli MBO e CNO sono anche superfici equivalenti, ossia hanno la stessa area.
$$ MBO \doteq CNO $$
Per semplificare il ragionamento, coloro di grigio le superfici equivalenti MBO e CNO.
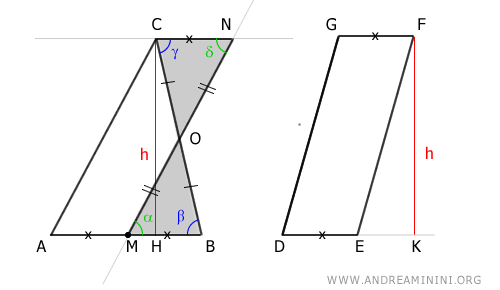
A questo punto il triangolo ABC posso vederlo come la somma del trapezio AMOC e il triangolo MBO.
$$ ABC \doteq AMOC + MBO $$
A sua volta il parallelogramma AMNC posso vederlo come somma tra il trapezio AMOC e il triangolo CNO.
$$ AMNC \doteq AMOC + CNO $$
Sapendo che i triangoli MBO e CNO sono equivalenti, deduco che il triangolo ABC e il parallelogramma AMNC sono equivalenti perché sono equicomposti dal trapezio AMC e da triangoli equivalenti CNO e MBO.
$$ ABC \doteq AMOC + MBO \doteq AMOC + CNO \doteq AMNC $$
$$ ABC \doteq AMNC $$

Poiché, il parallelogramma AMNC è equivalente al parallelogramma DEFG, deduco che anche il triangolo ABC e il parallelogramma DEFG hanno la superficie equivalente, ovvero la stessa area, e sono poligoni equivalenti.
$$ ABC \doteq DEFG $$
In questo modo ho dimostrato la prima parte del teorema.
A] Parallelogramma con stessa base e metà altezza del triangolo
Per dimostrare questa seconda parte del teorema, del tutto speculare alla prima, voglio seguire un ragionamento diverso dal precedente.
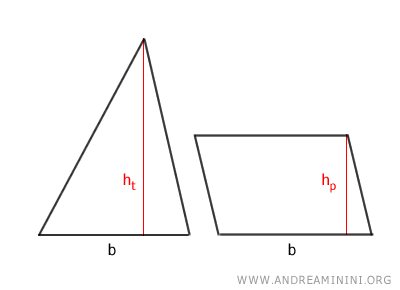
In questo caso il ragionamento è logico-matematico e si basa sul fatto che l'area del triangolo è il semiprodotto della base (bt) per l'altezza (ht)
$$ A_t = \frac{b_t \cdot h_t}{2} $$
Mentre l'area del parallelogramma è il prodotto della base (bp) per l'altezza (hp)
$$ A_p = b_p \cdot h_p $$
Ora, per ipotesi le basi del triangolo e del parallelogramma sono uguali
$$ b_p = b_t $$
Quindi, indicando la base comune con b=bt=bp le due formule dell'area diventano.
$$ A_t = \frac{b \cdot h_t}{2} $$
$$ A_p = b \cdot h_p $$
Il triangolo e il parallelogramma sono equivalenti quando hanno la stessa area.
$$ A_t = A_p $$
$$ \frac{b \cdot h_t}{2} = b \cdot h_p $$
Semplifico dividendo entrambi i membri per b
$$ \frac{b \cdot h_t}{2} \cdot \frac{1}{b} = b \cdot h_p \cdot \frac{1}{b} $$
$$ \frac{h_t}{2} = h_p $$
Pertanto, il triangolo e il parallelogramma hanno la stessa area quando l'altezza del parallelogramma $ h_p = \frac{h_t}{2} $ è uguale alla metà dell'altezza del triangolo.
Il teorema è dimostrato.
Nota. Questo ragionamento logico lo posso applicare anche per dimostrare la prima parte del teorema, quella in cui il triangolo e il parallelogramma hanno la stessa altezza. $$ A_t = \frac{b_t \cdot h_t}{2} $$ $$ A_p = b_p \cdot h_p $$ In questo caso l'altezza è la stessa h=ht=hp $$ A_t = \frac{b_t \cdot h}{2} $$ $$ A_p = b_p \cdot h $$ I due poligoni sono equivalenti quando hanno la stessa area $$ A_t = A_ p $$ $$ \frac{b_t \cdot h}{2} =b_p \cdot h $$ Semplifico l'equazione dividendo entrambi i membri per h. $$ \require{cancel} \frac{b_t \cdot \cancel{h}}{2} =b_p \cdot \cancel{h} $$ $$ \frac{b_t}{2} =b_p $$ Questo dimostra che i due poligoni hanno la stessa area quando la base del parallelogramma (bp) è la metà della base del triangolo (bt).
E così via.
