Il teorema dell'equivalenza fra un triangolo e un trapezio
Un trapezio è equivalente a un triangolo che ha la stessa altezza (h) e per base la somma delle due basi (B+b) del trapezio.
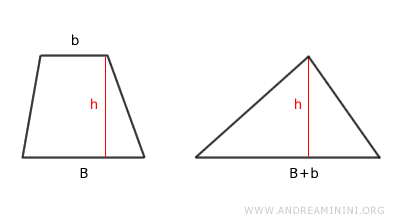
In altre parole, un trapezio e un triangolo hanno la stessa area se:
- l'altezza è congruente
- la base del triangolo è congruente con la somma delle basi del trapezio
In questo caso sono poligoni equivalenti.
Due poligoni sono detti poligoni equivalenti quando non si sovrappongono e si estendono su una superficie equivalente, ovvero quando hanno la stessa area.
Un esempio pratico
In questo esempio ho un triangolo e un trapezio che hanno la stessa altezza h=4.
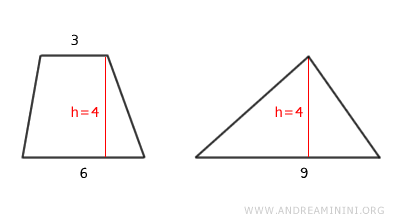
Il triangolo ha la base (9) congruente con la somma delle basi (6+3) del trapezio, quindi posso applicare il criterio di equivalenza.
L'area del triangolo è il semiprodotto della base e l'altezza.
$$ A_t = \frac{b \cdot h}{2} = \frac{9 \cdot 4}{2} = \frac{36}{2} = 18 $$
Essendo poligoni equivalenti, anche il trapezio ha la stessa area.
$$ A_z = 18 $$
Quindi, posso evitare di calcolarla.
Per verificare il risultato, calcolo l'area del trapezio anche usando la formula geometrica. L'area del trapezio è il semiprodotto tra la somma delle basi e l'altezza. $$ A_z = \frac{(B_z + b_z) \cdot h}{2} = \frac{(6 + 3) \cdot 4}{2} = \frac{9 \cdot 4}{2} = \frac{36}{2} = 18 $$ L'area è la stessa.
La dimostrazione
Considero un triangolo e un trapezio.
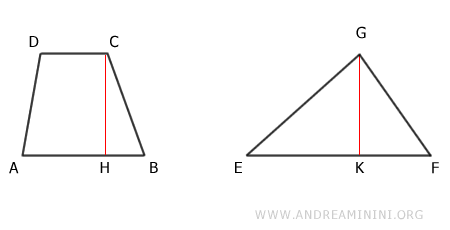
Per ipotesi iniziale, il triangolo e il trapezio hanno la stessa altezza.
$$ \overline{CH} \cong \overline{GK} $$
Inoltre, la somma delle due basi AB+CD del trapezio è congruente con la base EF del triangolo.
$$ \overline{AB} + \overline{CD} \cong \overline{EF} $$
Devo dimostrare che i poligoni sono equivalenti, ovvero che hanno la stessa area.
Per prima cosa prolungo la base AB del trapezio con un segmento BL di lunghezza pari alla base minore CD.
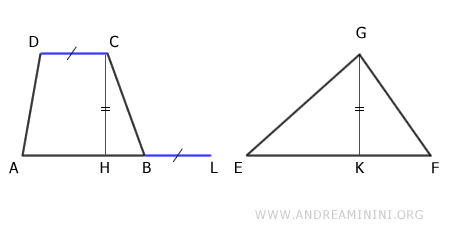
Poi traccio il segmento DL tra i punti D e L.
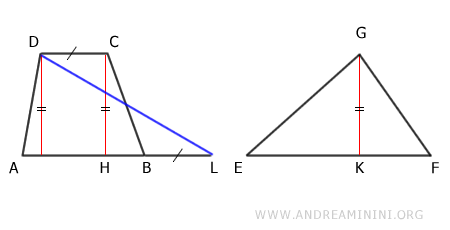
Il segmento AL è congruente con la base EF del triangolo perché
- BL≅CD per costruzione
- AB+CD≅EF per l'ipotesi iniziale, pertanto anche AB+BL≅EF
Quindi, il segmento AL≅EF è congruente con la base del triangolo
$$ \overline{AL} \cong \overline{EF} $$
In base al criterio di congruenza dei triangoli, il triangolo ADL è equivalente al triangolo EFG perché hanno la stessa altezza CH≅GK e la stessa base AL≅EF.
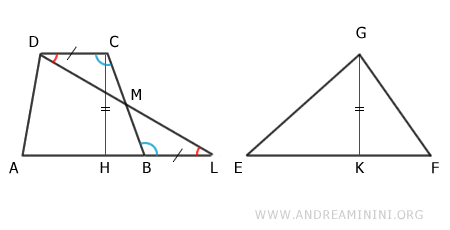
Anche i triangoli MCD e MBL sono congruenti perché
- Un trapezio ha sempre le basi parallele tra loro AB||CD e il segmento AL è semplicemente il prolungamento di AB.
- I segmenti BL≅CD sono congruenti per costruzione
- Gli angoli adiacenti alle basi BL e CD sono congruenti per il teorema delle rette parallele, perché sono angoli alterni interni di una trasversale tra due rette parallele.
Quindi, i triangoli MCD e MBL sono congruenti in base al secondo criterio di congruenza dei triangoli.
$$ MCD \cong MBL $$
Essendo i triangoli MCD e MBL congruenti, deduco che sono anche equivalenti ovvero hanno la stessa area.
$$ MCD \doteq MBL $$
Di conseguenza, posso vedere il trapezio ABCD come la somma del quadrilatero ABMD e del triangolo CDM.
$$ ABCD \doteq ABMD + MCD $$
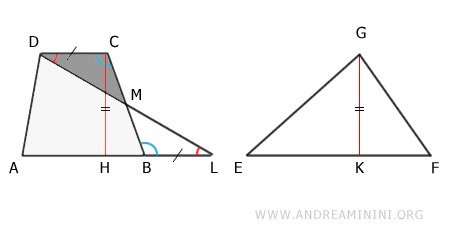
Allo stesso modo posso vedere il triangolo ADL come la somma del quadrilatero ABMD e del trianglo MBL.
$$ ADL \doteq ABMD + MBL $$
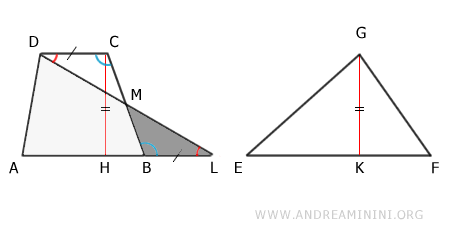
Poiché i triangoli MCD e MBL sono equivalenti, deduco che sia il trapezio che il triangolo sono composti dalle stesse superfici equivalenti.
$$ ABCD \doteq ABMD + MCD \doteq ABMD + MBL \doteq ADL $$
Di conseguenza, essendo equicomposti, il trapezio ABCD e il triangolo ADL sono poligoni equivalenti.
$$ ABCD \doteq ADL $$
Sapendo anche che il triangolo ADL è equivalente al triangolo EFG, deduco che il trapezio ABCD e il triangolo EFG sono equivalenti.
$$ ABCD \doteq ADL \doteq EFG $$
$$ ABCD \doteq EFG $$
In questo modo ho dimostrato il teorema iniziale.
Dimostrazione alternativa
Provo a dimostrare il teorema seguendo un ragionamento logico-matematico.
L'area del triangolo è il semiprodotto della base per l'altezza
$$ A_t = \frac{b_t \cdot h_t}{2} $$
L'area del trapezio è il prodotto tra la somma delle basi e l'altezza, diviso due.
$$ A_z = \frac{(B_z+b_z) \cdot h_z}{2} $$
Devo dimostrare in quali condizioni il triangolo e il trapezio hanno la stessa area
$$ A_t = A_z $$
$$ \frac{b_t \cdot h_t}{2} = \frac{(B_z+b_z) \cdot h_z}{2} $$
Per ipotesi i due poligoni hanno la stessa altezza ht=hz
$$ \frac{b_t \cdot h_t}{2} = \frac{(B_z+b_z) \cdot h_t}{2} $$
Inoltre, per ipotesi la somma delle basi del trapezio Bz+bz è congruente con la base del triangolo bt
$$ \frac{b_t \cdot h_t}{2} = \frac{b_t \cdot h_t}{2} $$
Le due formule sono uguali.
Questo dimostra che il triangolo e il trapezio hanno la stessa area, ovvero sono equivalenti, quando hanno la stessa altezza e la somma delle basi del trapezio è uguale alla base del triangolo.
E così via.
