Teorema della proporzionalità delle basi e altezze nei triangoli simili

In due triangoli simili il rapporto tra le basi è uguale al rapporto tra le altezze, ovvero le basi e le altezze sono proporzionali.

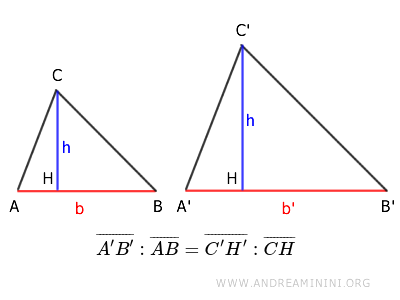
Questo teorema stabilisce la proporzionalità tra le corrispondenti basi e altezze di due triangoli simili.

E' un'altra importante proprietà dei triangoli simili: non solo i lati, ma anche le altezze rispettano la stessa proporzione.

Un esempio pratico

Prendo come esempio due triangoli simili ABC e A'B'C'.

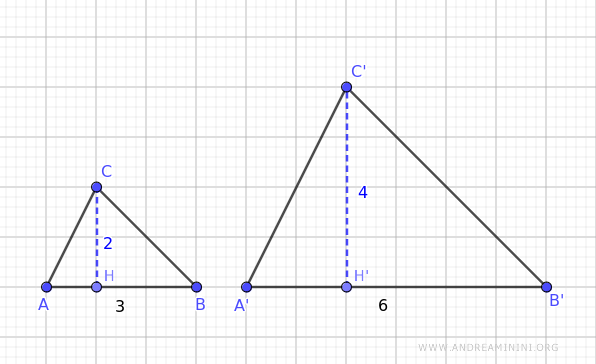
Considero come base del triangolo ABC il segmento AB e come base del triangolo A'B'C il lato corrispondente A'B'

Il rapporto tra le basi dei due triangoli simili è uguale a 2.

$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{6}{3} = 2 $$

Ora calcolo il rapporto tra le relative altezze dei due triangoli rispetto alle basi AB e A'B'

$$ \frac{ \overline{C'H'} }{ \overline{CH} } = \frac{4}{2} = 2 $$

Anche il rapporto tra le altezze è uguale a 2 ovvero è uguale al rapporto delle relative basi.

Quindi, le altezze stanno fra loro come le rispettive basi.

Nota. Questa proprietà vale solo se i due triangoli sono simili.

Lo stesso vale se prendo come base altri due lati corrispondenti dei due triangoli simili e le relative altezze.

Ad esempio, prendo come base i lati BC e B'C' dei due triangoli e le relative altezze AH e A'H'.

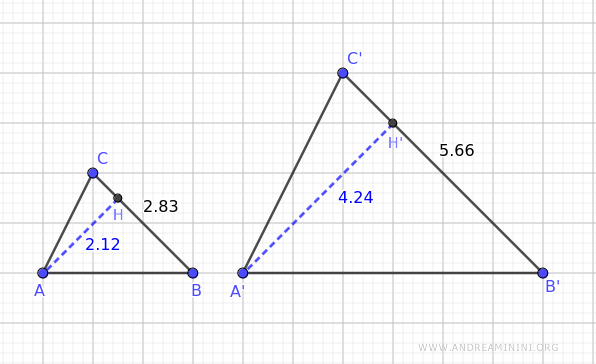
Il rapporto tra le basi dei due triangoli simili è  1.33.

$$ \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{5.66}{4.24} = 1.33 $$

Il rapporto tra le altezze dei due triangoli simili è sempre  1.33.

$$ \frac{ \overline{A'H'} }{ \overline{AH} } = \frac{2.83}{2.12} = 1.33 $$

Il risultato finale è sempre lo stesso. Nei triangoli simili le basi stanno fra loro come le rispettive altezze, e viceversa.

 

La dimostrazione

Considero due triangoli simili ABC e A'B'C'.

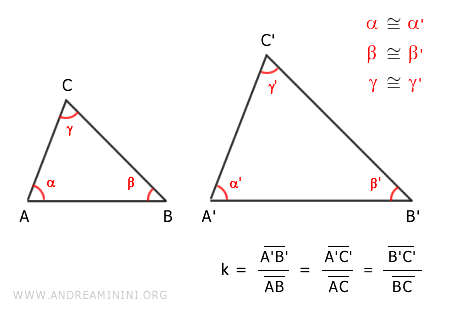
Essendo simili, i due triangoli hanno gli angoli congruenti α≅α', β≅β', γ≅γ' e i lati corrispondenti proporzionali

$$ \overline{A'B'} : \overline{AB} = \overline{A'C'} : \overline{AC} = \overline{B'C'} : \overline{BC} $$

In altre parole esiste un fattore di proporzionalità k comune tra i lati corrispondenti dei triangoli

$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{A'C'} }{ \overline{AC} } = \frac{ \overline{B'C'} }{ \overline{BC} } = k $$

Considero come base del triangolo ABC il segmento AB e come base del triangolo A'B'C' il lato corrispondente A'B'.

Quindi, le relative altezze sono i segmenti CH e C'H'.

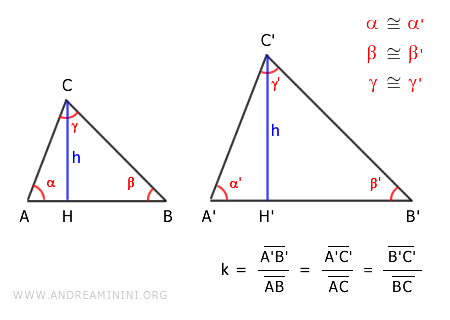
Analizzo i triangoli rettangoli ACH e A'C'H' formati dall'altezza nei due triangoli.

In base al primo criterio di similitudine dei triangoli, i triangoli rettangoli ACH e A'C'H' sono simili, perché hanno i lati proporzionali e l'angolo tra di essi congruente α≅α'.

$$ ACH \approx A'C'H' $$

Essendo simili, i triangoli rettangoli ACH e A'C'H' hanno tutti i lati proporzionali.

$$ \overline{A'C'} : \overline{AC} =  \overline{C'H'} : \overline{CH} $$

Dove AC e A'C' sono lati corrispondenti dei due triangoli ABC e A'B'C' mentre CH e C'H' sono le relative altezze.

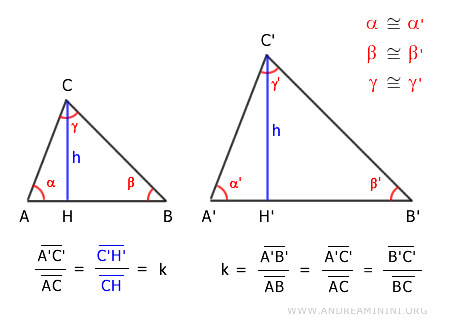
Sapendo che i lati due due triangoli ABC e A'B'C' sono proporzionali, poiché i triangoli sono simili, deduco che le altezze hanno la stessa proporzione delle basi

$$ \overline{A'B'} : \overline{AB} =  \overline{C'H'} : \overline{CH} $$

Questo dimostra che i due triangoli simili hanno le basi e altezze proporzionali.

E così via.