Il terzo criterio di similitudine dei triangoli
Due triangoli sono simili se hanno i lati in proporzione nello stesso ordine.
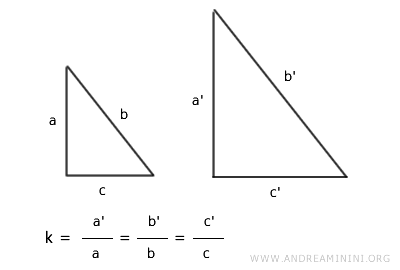
Secondo questo criterio, quando due triangoli hanno i lati ordinatamente proporzionali formano due figure simili.
Questo criterio di similitudine dei triangoli è anche noto come LLL (Lato-Lato-Lato).
Un esempio pratico
Considero due triangoli ABC e A'B'C' con i lati proporzionali nello stesso ordine.
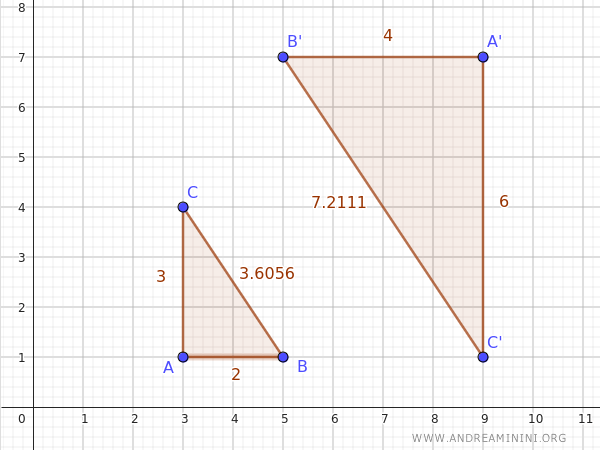
In questo caso il rapporto di proporzionalità è pari a 2.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{4}{2} = 2 $$
$$ \frac{ \overline{A'C'} }{ \overline{AC} } = \frac{6}{3} = 2 $$
$$ \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{7.2}{3.6} = 2 $$
Secondo il terzo criterio di similitudine dei triangoli, i due triangoli ABC e A'B'C' sono triangoli simili.
$$ ABC \approx A'B'C' $$
In effetti i due triangoli sono simili perché hanno tutti gli angoli congruenti nello stesso ordine.
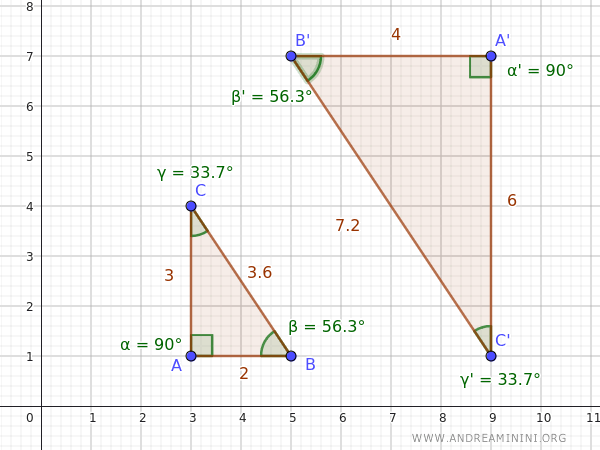
Quindi, hanno la stessa forma ma una dimensione diffente.
La dimostrazione
Considero due triangoli ABC e A'B'C'
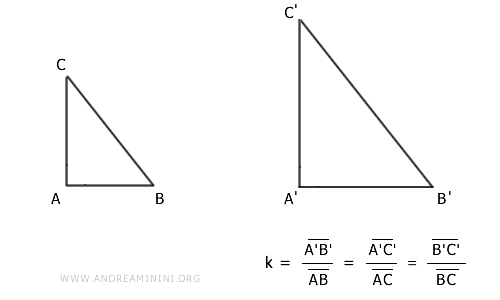
Per ipotesi i lati dei due triangoli sono proporzionali nello stesso ordine
$$ \overline{A'B'}:\overline{AB} = \overline{B'C'}:\overline{BC} = \overline{A'C'}:\overline{AC} $$
Esprimo la proporzione nella forma equivalente di una uguaglianza tra frazioni.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k $$
Il rapporto di proporzionalità è pari a k.
Devo dimostrare la similitudine tra i due triangoli.
$$ ABC \approx A'B'C' $$
Per farlo analizzo due casi: quello in cui i lati AC=A'C' sono congruenti e il caso opposto in cui non sono congruenti.
1] I lati AB e A'B' sono congruenti
In questo caso i lati AB≅A'B' sono congruenti
$$ \overline{A'B'} \cong \overline{AB} $$
Questo vuol dire che hanno la stessa lunghezza. Pertanto, il rapporto di proporzionalità è pari a k=1.
$$ k = \frac{ \overline{A'B'} }{ \overline{AB} } = 1 $$
Ciò significa che anche gli altri due lati hanno lo stesso rapporto di proporzionalità
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k=1 $$
Pertanto, tutti i lati dei triangoli sono congruenti nello stesso ordine.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
Per il terzo criterio di congruenza dei triangoli, i due triangoli ABC e A'B'C' sono congruenti perché hanno tutti i lati corrispondenti congruenti.
$$ ABC \cong A'B'C' $$
Due figure congruenti sono anche simili, con un rapporto di similitudine uguale a k=1, quindi triangoli ABC e A'B'C' sono simili.
2] I lati AB e A'B' non sono congruenti
In questo caso i lati AB e A'B' non sono congruenti, quindi hanno una lunghezza differente.
Questo vuol dire che il rapporto di proporzionalità tra i due segmenti è diverso da 1.
$$ k = \frac{ \overline{A'C'} }{ \overline{AC} } \ne 1 $$
Quindi, anche gli altri lati corrispondenti dei due triangoli non sono congruenti
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k \ne 1 $$
A questo punto utilizzo lo stesso rapporto k per costruire un'omotetia sul triangolo ABC prendendo il punto A come centro dell'omotetia.
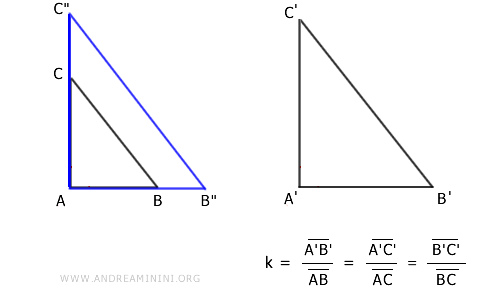
In questo modo ottengo il triangolo A"B"C" ovvero una trasformata omotetica del triangolo ABC.
I triangoli A"B"C" e ABC sono simili perché ogni trasformata omotetica di una figura genera una figura simile.
$$ A"B"C" \approx ABC $$
Il rapporto k dell'omotetia che ho scelto è appositamente uguale al rapporto di proporzione tra i lati corrispondenti dei due triangoli ABC e A'B'C'.
$$ \frac{ \overline{A'B'} }{ \overline{AB} } = \frac{ \overline{B'C'} }{ \overline{BC} } = \frac{ \overline{A'C'} }{ \overline{AC} } = k $$
Ne consegue che il triangolo omotetico A"B"C" ha i lati corrispondenti della stessa lunghezza del triangolo A'B'C'.
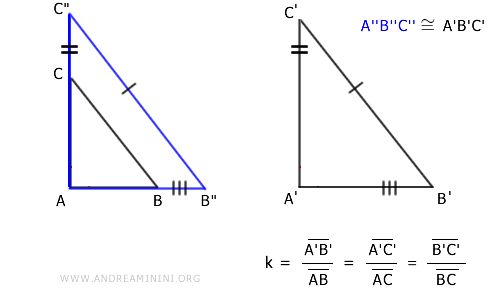
Pertanto, per il terzo criterio di congruenza dei triangoli, i due triangoli A"B"C" e A'B'C' sono congruenti.
$$ A'B'C' \cong A''B''C'' $$
Essendo congruenti, i due triangoli sono anche simili con un rapporto di similitudine k=1.
$$ A'B'C' \approx A''B''C'' $$
Sapendo che il triangolo A'B'C' a sua volta è simile al triangolo ABC, perché è una trasformata omotetica di quest'ultimo, deduco che anche i triangoli A'B'C' e ABC sono simili.
$$ A'B'C' \approx A''B''C'' \approx ABC $$
Pertanto, anche in questo caso i triangoli A'B'C' e ABC sono simili.
3) Conclusione
In entrambe le ipotesi, i lati AB e A'B' congruenti e non congruenti, i triangoli ABC e A'B'C' sono figure simili.
Questo dimostra il terzo criterio di similitudine dei triangoli.
E così via.
