Esercizio sottospazio vettoriale 3
Nello spazio vettoriale V=R2 devo verificare se il seguente sottoinsieme W è un sottospazio vettoriale di V oppure no. $$ W = \{ (x,y) \ | \ x^2-y=0 \ \} $$
Per essere un sottospazio vettoriale deve soddisfare le proprietà dei sottospazi vettoriali e degli spazi vettoriali..
1) Presenza dell'elemento nullo in W
Considero un generico vettore del sottoinsieme W
$$ \vec{w} = \begin{pmatrix} x \\ y \end{pmatrix} \ \in \ W \Leftrightarrow x^2-y=0 $$
Poi verifico se il sottospazio include l'elemento nullo (x,y)=(0,0)
$$ x^2-y=0 $$
$$ (0)^2-(0)=0 $$
$$ 0 = 0 $$
L'elemento nullo esiste nel sottoinsieme.
Pertanto, non posso subito escludere che sia uno spazio vettoriale.
Nota. La verifica dell'elemento nullo è molto utile farla all'inizio dell'esercizio perché se non ci fosse l'elemento nullo l'insieme W non sarebbe uno spazio vettoriale e, di conseguenza, nemmeno un sottospazio vettoriale. L'esercizio finirebbe qui.
2) La chisura rispetto alla somma dei vettori di W
Prendo due vettori generici del sottoinsieme W
$$ \forall \vec{w}_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \ \in \ \Leftrightarrow x^2_1-y_1=0 $$
$$ \forall \vec{w}_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} \ \in \ \Leftrightarrow x^2_2-y_2=0 $$
Entrambe le coppie di numeri reali (x1,y1) e (x2,y2) soddisfano l'equazione x2-y=0 del sottoinsieme W.
Verifico se la somma dei due vettori appartiene a W.
$$ (x_1+x_2)^2 - (y_1+y_2) = 0 $$
$$ x_1^2+2x_1x_2 + x_2^2 - y_1-y_2 = 0 $$
$$ (x_1^2-y_1) + (x_2^2 -y_2) + 2x_1x_2 = 0 $$
Sapendo che x12-y1 è uguale a zero perché il vettore w1 è x12-y1=0
$$ (0) + (x_2^2 -y_2) + 2x_1x_2 = 0 $$
e che x22-y2 è uguale a zero perché il vettore w2 è x22-y2=0
$$ (0) + (0) + 2x_1x_2 = 0 $$
$$ 2x_1x_2 = 0 $$
Questa identità non è verificata in generale quando x1≠0 e x2≠0
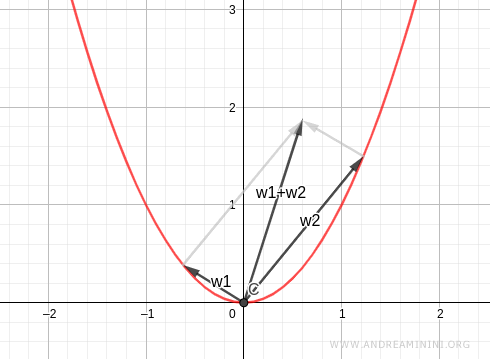
La somma w1+w2 non appartiene a W.
Pertanto, il sottoinsieme W non è chiuso rispetto alla somma dei vettori.
$$ \vec{w}_1 + \vec{w}_2 \notin W $$
La prima proprietà dei sottospazi vettoriali non è soddisfatta
Quindi, l'insieme W non è un sottospazio vettoriale.
Nota. Dal punto di vista geometrico il sottoinsieme di vettori x2-y=0 non è una retta bensì una parabola. Qualsiasi somma di vettori diversi dal vettore nullo non appartiene alla parabola.
E così via.
