Sottospazi vettoriali e combinazioni lineari
Dato uno spazio vettoriale V nel campo K e un sottoinsieme W di V, il sottoinsieme W è un sottospazio vettoriale di W se è chiuso rispetto alle combinazioni lineari.
Se per ogni
$$ w_1,...,w_m \in W $$ $$ a_1,...,a_m \in K $$
allora
$$ a_1 w_1 + ... + a_m w_m \in W $$
La dimostrazione
Dire che la combinazione lineare appartiene a W riassume le due proprietà ( chiusura della somma e del prodotto ) che definiscono un sottospazio vettoriale.
- Dati due elementi qualsiasi w1 e w2 di W, anche la loro somma w1+w2 appartiene all'insieme W
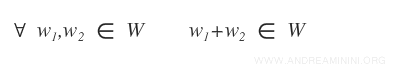
- Dato uno scalare λ qualsiasi appartenente al campo K e un elemento qualsiasi w dell'insieme W, anche il prodotto λw appartiene all'insieme W.
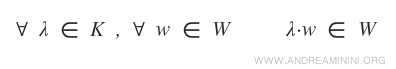
Pertanto, anche il risultato della combinazione lineare è un elemento dello spazio vettoriale V.
E' quindi un sottospazio vettoriale di V.
L'insieme Lk di tutte le combinazioni lineari
Dati m vettori v1,...vm dello spazio vettoriale V sul campo K, si indica con Lk l'insieme di tutte le combinazioni lineari degli m vettori con i coefficienti α di K.
$$ L_k \{ v_1 , ..., v_m \} = \{ α_1 \cdot v_1 + ... + α_m \cdot v_m , \forall α_1,...,α_m \in K \} $$
L'insieme di tutte le combinazioni lineari Lk è un sottospazio vettoriale di V perché è chiuso alle combinazioni lineari.
Ogni combinazione lineare è chiusa rispetto alla somma e al prodotto, quindi è un sottospazio vettoriale di V.
L'insieme Lk è il sottospazio vettoriale più piccolo contenente i vettori v1,...,vk.
Nota. Nei testi di algebra lineare l'insieme Lk può essere indicato in modi diversi. Ad esempio, Link o spank
