Esercizio sui vettori generatori dello spazio vettoriale 1
Considero due vettori nello spazio vettoriale V=R3
$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$
I due vettori sono generatori di R3?
Devo verificare se posso scrivere un generico vettore v di R3
$$ v = \begin{pmatrix} a \\ b \\ c \end{pmatrix} \ \in V = R^3 $$
come combinazione lineare dei vettori v1 e v2
$$ \vec{v} = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$
$$ \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$
Trasformo l'equazione vettoriale in un sistema di tre equazioni e due incognite.
$$ \begin{cases} \lambda_1 + 0 = a \\ 2 \lambda_1 + 3 \lambda_2 = b \\ - \lambda_1 + \lambda_2 = c \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 \lambda_1 + 3 \lambda_2 = b \\ - \lambda_1 + \lambda_2 = c \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 \lambda_2 = b \\ - a + \lambda_2 = c \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 \lambda_2 = b \\ \lambda_2 = c+a \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 (c+a) = b \\ \lambda_2 = c+a \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 2 a + 3c + 3a = b \\ \lambda_2 = c+a \end{cases} $$
$$ \begin{cases} \lambda_1 = a \\ 5 a + 3c = b \\ \lambda_2 = c+a \end{cases} $$
Il sistema di equazioni ha soluzioni soltanto se 5a+3c=b
Quindi, non ha soluzioni per qualsiasi valore di a, b, c.
Questo vuol dire che i due vettori v1 e v2 non possono generare tutti i vettori v(a,b,c) dello spazio vettoriale V=R3
Pertanto, i due vettori v1 e v2 non sono generatori dello spazio vettoriale V=R3
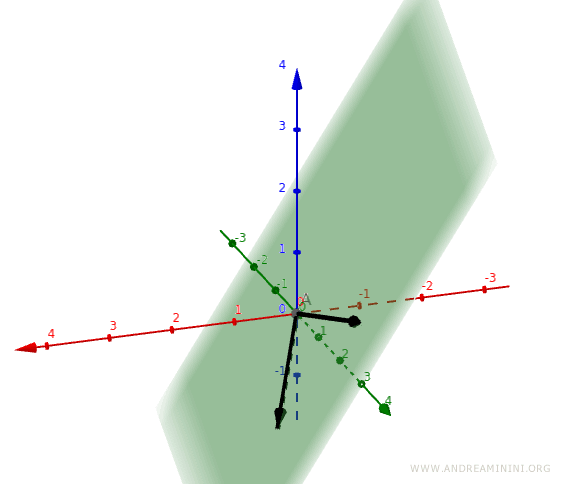
Nota. Del resto due vettori linearmente indipendenti come v1 e v2 possono generare solo tutti i vettori del piano R2 in cui risiedono. In questo caso lo spazio vettoriale è di dimensioni più grandi R3. Due soli vettori non possono generare tutti i vettori di uno spazio a tre dimensioni. Per riuscirci servono almeno tre vettori linearmente indipendenti.
E così via.
