Le operazioni tra numeri razionali
Nell'insieme dei numeri razionali Q sono definite le seguenti operazioni
Addizione
La somma di due razionali rappresentati da due frazioni con lo stesso denominatore è una frazione che ha lo stesso denominatore e per numeratore la somma dei numeratori. $$ \frac{a}{b} + \frac{c}{b} = \frac{a+c}{b} $$
Esempio. La somma tra i numeri razionali 3/2 e 5/2 $$ \frac{3}{2} + \frac{5}{2} = \frac{3+5}{2} = \frac{8}{2} $$
Se i numeri razionali hanno denominatori differenti, prima riduco le due frazioni allo stesso denominatore comune, poi sommo i numeratori.
Esempio. I numeri razionali 3/2 e 5/3 hanno un diverso denominatore. $$ \frac{3}{2} + \frac{5}{3} $$ Il minimo comune multiplo dei denominatori è mcm(2,3)=6. Applico la proprietà invariantiva delle frazioni per trasformarle in due frazioni equivalenti con denominatore uguale a 6. $$ \frac{3 \cdot 3}{2 \cdot 3} + \frac{5 \cdot 2}{3 \cdot 2} $$ $$ \frac{9}{6} + \frac{10}{6} $$ Ora le frazioni hanno lo stesso denominatore. Quindi, posso sommare i numeratori. $$ \frac{9}{6} + \frac{10}{6} = \frac{9+10}{6} = \frac{19}{6} $$
L'addizione è un'operazione interna all'insieme dei numeri razionali, perché la somma di due numeri razionali è sempre un altro numero razionale.
$$ a+b = c \ \in Q \ \ \ \forall \ a,b \in Q $$
Nell'insieme dei numeri razionali l'addizione soddisfa la proprietà commutativa e associativa.
$$ a+b=b+a \ \ \ \ \forall \ a,b \in Q $$
$$ a+(b+c)=(a+b)+c \ \ \ \ \forall \ a,b,c \in Q $$
L'elemento neutro dell'addizione è lo zero perché la somma di ogni numero razionale e zero è sempre uguale a zero.
$$ a+0=0+a=a \ \ \ \ \forall \ a \in Q $$
Per ogni numero razionale esiste un elemento opposto dell'addizione tale che la somma dei due numeri è uguale all'elemento neutro (0)
$$ a + (-a) = 0 $$
Esempio. Il numero opposto di 2/3 è -2/3 $$ \frac{2}{3} - \frac{2}{3} = \frac{2-2}{3} = \frac{0}{3} = 0 $$
Sottrazione
La sottrazione di due razionali rappresentati da due frazioni con lo stesso denominatore è una frazione che ha lo stesso denominatore e per numeratore la differenza dei numeratori. $$ \frac{a}{b} - \frac{c}{b} = \frac{a-c}{b} $$
Esempio. La differenza tra i numeri razionali 5/2 e 3/2 $$ \frac{5}{2} - \frac{3}{2} = \frac{5-3}{2} = \frac{2}{2} = 1 $$
Se i numeri razionali hanno denominatori diversi, devo prima effettuare la riduzione delle frazioni allo stesso denominatore comune.
Dopo aver ridotto le due frazioni allo stesso denominatore, posso calcolare la differenza tra i numeratori.
Esempio. I numeri razionali 5/2 e 2/3 hanno un diverso denominatore. $$ \frac{5}{2} - \frac{2}{3} $$ Il minimo comune multiplo dei denominatori è mcm(2,3)=6. Applico la proprietà invariantiva delle frazioni per trasformarle in due frazioni equivalenti con denominatore uguale a 6. $$ \frac{5 \cdot 3}{2 \cdot 3} - \frac{2 \cdot 2}{3 \cdot 2} $$ $$ \frac{15}{6} - \frac{4}{6} $$ Ora le frazioni hanno lo stesso denominatore. Quindi, posso sottrarre i numeratori ossia sommare il primo numeratore con l'opposto del secondo numeratore. $$ \frac{15}{6} - \frac{4}{6} = \frac{15-4}{6} = \frac{11}{6} $$
La sottrazione è un'operazione interna all'insieme dei numeri razionali, perché la differenza di due numeri razionali è sempre un altro numero razionale.
$$ a-b = c \ \in Q \ \ \ \forall \ a,b \in Q $$
Nell'insieme dei numeri razionali la differenza soddisfa la proprietà invariantiva.
Sommando o sottraendo lo stesso valore (c) dal minuendo (a) e dal sottraendo (b) la differenza a-b non cambia.
$$ a-b = (a+c) - (b+c) \ \ \ \forall \ a,b,c \in Q $$
$$ a-b = (a-c) - (b-c) \ \ \ \forall \ a,b,c \in Q $$
Moltiplicazione
Il prodotto di due numeri razionali espressi in frazioni è una frazione che ha per numeratore il prodotto dei numeratori e per denominatore il prodotto dei denominatori $$ \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} $$
Esempio. Il prodotto tra 3/2 e 5/2 $$ \frac{3}{2} \cdot \frac{5}{2} = \frac{3 \cdot 5}{2 \cdot 2} = \frac{15}{4} $$
Il prodotto tra frazioni equivalenti è sempre lo stesso.
Esempio. Le frazioni 6/4 e 10/4 sono equivalenti rispettivamente a 3/2 e 5/2. Il prodotto è lo stesso. $$ \frac{6}{4} \cdot \frac{10}{4} = \frac{6 \cdot 10}{4 \cdot 4} = \frac{60}{16} = \frac{15}{4} $$
La moltiplicazione è un'operazione interna all'insieme dei numeri razionali perché la somma di due numeri razionali è un altro numero razionale
$$ a \cdot b = c \in Q \ \ \forall \ a,b \in Q $$
Nella moltiplicazione dei numeri razionali vale la regola dei segni dei numeri interi.
Il prodotto tra due numeri concordi è positivo (più) mentre quello tra due numeri discordi è negativo (meno).
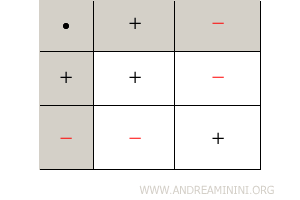
La moltiplicazione soddisfa la proprietà commutativa.
$$ a \cdot b = b \cdot a $$
Esempio. Il prodotto tra 5/2 e 3/4 è uguale al prodotto tra 3/4 e 5/2 $$ \frac{5}{2} \cdot \frac{3}{4} = \frac{3}{4} \cdot \frac{5}{2} = \frac{15}{8} $$
La moltiplicazione soddisfa la proprietà associativa.
$$ a \cdot ( b \cdot c) = (b \cdot a) \cdot c $$
Esempio. Ecco un esempio pratico $$ \frac{6}{4} \cdot ( \frac{1}{2} \cdot \frac{2}{4} ) = ( \frac{6}{4} \cdot \frac{1}{2} ) \cdot \cdot \frac{2}{4} $$
La moltiplicazione soddisfa la proprietà distributiva all'addizione.
$$ a \cdot ( b + c) = a \cdot b + a \cdot c $$
Esempio. Ecco un esempio pratico $$ \frac{6}{4} \cdot ( \frac{1}{2} + \frac{2}{4} ) = \frac{6}{4} \cdot \frac{1}{2} + \frac{6}{4} \cdot \frac{2}{4} $$
L'elemento neutro della moltiplicazione è il numero 1 perché il prodotto di qualsiasi numero razionale per uno è uguale al numero stesso.
$$ \forall \ a \in Q \Rightarrow a \cdot 1 = a $$
Esempio. Il prodotto tra 4/3 e +1 è uguale a 4/3. $$ \frac{4}{3} \cdot 1 = \frac{4 \cdot 1}{3 \cdot 1} = \frac{4}{3} $$
L'elemento assorbente della moltiplicazione è il numero 0 perché il prodotto di qualsiasi numero razionale per zero è uguale a zero.
$$ \forall \ a \in Q \Rightarrow a \cdot 0 = 0 $$
Pertanto, nella moltiplicazione dei numeri razionali vale la legge di annullamento del prodotto.
Esempio. Il prodotto tra 4/3 e 0 è uguale a zero. $$ \frac{4}{3} \cdot 0 = \frac {4}{3} \cdot \frac{0}{1} = \frac{4 \cdot 0}{3 \cdot 1} = \frac{0}{3} = 0 $$ Voglio sottolineare un aspetto che spesso è un errore frequente. Qualsiasi numero intero n espresso in frazioni si scrive n/1. $$ n = \frac{n}{1} $$ Quindi, il numero 0 espresso in frazione si scrive 0/1, non si scrive 0/0. $$ 0 = \frac{0}{1} $$
Qualsiasi numero razionale moltiplicato per -1 è uguale al suo numero opposto ossia all'elemento opposto dell'addizione.
$$ \forall \ \frac{a}{b} \in Q \ , \ a,b \in Z \Rightarrow \frac{a}{b} \cdot ( -1 ) = - \frac{a}{b} $$
Esempio. Il prodotto tra 1/2 e -1 è uguale a -1/2 $$ \frac{1}{2} \cdot (-1) = \frac{1}{2} \cdot ( \frac{-1}{1} ) = \frac{1 \cdot (-1)}{2 \cdot 1} = - \frac{1}{2} $$ Dove -1/2 è l'elemento opposto di 1/2 perché la loro somma è uguale a zero $$ \frac{1}{2} + ( - \frac{1}{2} ) = \frac{1}{2} - \frac{1}{2} = 0 $$
Per ogni numero razionale non nullo esiste un elemento inverso della moltiplicazione, detto reciproco, tale che il prodotto dei due numeri è uguale all'elemento neutro della moltiplicazione ossia a 1.
$$ \frac{a}{b} \cdot \frac{b}{a} = 1 $$
Quindi, per trovare il reciproco di un numero razionale basta scambiare il numeratore con il denominatore.
Esempio. Il reciproco di 5/2 è il numero razionale 2/5 $$ \frac{5}{2} \cdot \frac{2}{5} = 1 $$
L'unico numero razionale senza un elemento opposto è il numero zero, perché il reciproco di zero causerebbe una divisione per zero ossia un'operazione impossibile. $$ \frac{0}{1} \cdot \color{red}{ \frac{1}{0} } = impossibile $$
Divisione
La divisione tra due numeri razionali, con il secondo diverso da zero, è un numero razionale (detto quoziente) uguale al prodotto del primo per il reciproco del secondo $$ \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} $$
Esempio. La divisione tra 5/2 e 3/2 è uguale a 5/3 $$ \frac{ \frac{5}{2} }{ \frac{3}{2} } = \frac{5}{2} \cdot \frac{2}{3} = \frac{5}{3} $$
La divisione è l'operazione inversa della moltiplicazione.
Pertanto, valgono le stesse regole del segno della moltiplicazione.

La divisione è un'operazione interna nell'insieme dei numeri razionali perché il quoziente di due numeri razionali è un altro numero razionale.
$$ \forall \ n,m \ \in Q \ , \ m \ne 0 \ \Rightarrow \frac{n}{m}
\in Q $$
La divisione non è ammessa se il divisore è uguale a zero, perché la divisione per zero è un'operazione impossibile in matematica.
$$ \frac{n}{0} = \text{impossibile} \ \ n \ \in Q $$
Nel caso particolare in cui sia il numeratore che il denominatore sono nulli, l'operazione è indefinita
$$ \frac{0}{0} = \text{indefinita} $$
La divisione tra due numeri razionali soddisfa la proprietà distributiva a destra rispetto all'addizione.
$$ (n+m):p = n:p + m:p \ \ \ \ n,m,p \ \in Q $$
Esempio. La somma di 5/2 + 3/2 divisa per 1/2 è uguale alla somma dei quozienti 5/2 : 1/2 e 3/2 : 1/2 $$ ( \frac{5}{2} + \frac{3}{2} ) : \frac{1}{2} = \frac{5}{2} : \frac{1}{2} + \frac{3}{2}: \frac{1}{2} $$ Svolgendo i passaggi algebrici in entrambi i membri ottengo lo stesso risultato $$ ( \frac{8}{2} ) : \frac{1}{2} = \frac{5}{2} \cdot \frac{2}{1} + \frac{3}{2} \cdot \frac{2}{1} $$ $$ \frac{8}{2} \cdot \frac{2}{1} = \frac{10}{2} + \frac{6}{2} $$ $$ \frac{16}{2} = \frac{16}{2} $$
Non soddisfa la proprietà distributiva della moltiplicazione rispetto all'addizione a sinistra
$$ p:(n+m) \ne p:n + p:q$$
Esempio. Il quoziente tra 1/2 e la somma di 5/2 + 3/2 non è detto che sia uguale alla somma dei quozienti 1/2 : 5/2 e 1/2 : 3/2 $$ \frac{1}{2} : ( \frac{5}{2} + \frac{3}{2} ) \ne \frac{1}{2} : \frac{5}{2} + \frac{1}{2}: \frac{5}{2} $$ Svolgendo i passaggi algebrici in entrambi i membri ottengo un risultato diverso $$ \frac{1}{2} : ( \frac{8}{2} ) \ne \frac{1}{2} \cdot \frac{2}{5} + \frac{1}{2} \cdot \frac{2}{5} $$ $$ \frac{1}{2} \cdot \frac{2}{8} \ne \frac{1}{5} + \frac{1}{5} $$ $$ \frac{1}{8} \ne \frac{2}{5} $$
La divisione tra numeri razionali soddisfa la proprietà invariantiva.
Se moltiplico o divido il dividendo e il divisore per uno stesso numero razionale diverso da zero, il quoziente non cambia.
$$ n:m = (n \cdot p):(m \cdot p) = (n : p):(m : p) \ \ \ \ n,m,p \ \in Q \ , \ p \ne 0 $$
Esempio. Nella divisione tra 5/2 e 3/2 moltiplico il dividendo e il divisore per 1/2 $$ \frac{5}{2} : \frac{3}{2} = ( \frac{5}{2} \cdot \frac{1}{2} ) : ( \frac{3}{2} \cdot \frac{1}{2} ) $$ Svolgendo i passaggi algebrici in entrambi i membri, ottengo lo stesso risultato $$ \frac{5}{2} \cdot \frac{2}{3} = ( \frac{5}{4} ) : ( \frac{3}{4} ) $$ $$ \frac{5}{3}= \frac{5}{4} \cdot \frac{4}{3} $$ $$ \frac{5}{3}= \frac{5}{3} $$ Lo stesso accade se divido il dividendo e il divisore per 1/2 $$ \frac{5}{2} : \frac{3}{2} = ( \frac{5}{2} : \frac{1}{2} ) : ( \frac{3}{2} : \frac{1}{2} ) $$ $$ \frac{5}{2} \cdot \frac{2}{3} = ( \frac{5}{2} \cdot \frac{2}{1} ) : ( \frac{3}{2} \cdot \frac{2}{1} ) $$ $$ \frac{5}{3} = \frac{5}{1} : \frac{3}{1} $$ $$ \frac{5}{3} = \frac{5}{1} \cdot \frac{1}{3} $$ $$ \frac{5}{3} = \frac{5}{3} $$
L'elemento neutro della divisione è il numero 1 perché qualsiasi numero razionale diviso per uno è uguale al numero stesso
$$ \forall \ \frac{a}{b} \in Q \ , \ a,b \in Z \Rightarrow \frac{ \frac{a}{b} }{1} = \frac{a}{b} \cdot \frac{1}{1} = \frac{a}{b} $$
Dove 1 è un numero intero e posso scriverlo anche sotto forma di frazione 1/1.
Esempio. Il quoziente tra 1/2 e 1 è uguale a 1/2 $$ \frac{1}{2} : 1 = \frac{1}{2} : \frac{1}{1} = \frac{1}{2} \cdot \frac{1}{1} = \frac{1 \cdot 1}{2 \cdot 1} = \frac{1}{2} $$
Pertanto, qualsiasi numero razionale diviso per se stesso è uguale a 1.
$$ \forall \ \frac{a}{b} \in Q \ , \ a,b \in Z \Rightarrow \frac{ \frac{a}{b} }{ \frac{a}{b} } = \frac{a}{b} \cdot \frac{b}{a} = 1 $$
Esempio. Il quoziente tra 1/2 e 1/2 è uguale a 1 $$ \frac{1}{2} : \frac{1}{2} = \frac{1}{2} \cdot \frac{2}{1} = \frac{1 \cdot 2}{2 \cdot 1} = \frac{2}{2} = 1 $$
Qualsiasi numero razionale diviso per -1 è uguale al suo numero opposto ossia all'elemento opposto dell'addizione.
$$ \forall \ \frac{a}{b} \in Q \ , \ a,b \in Z \Rightarrow \frac{ \frac{a}{b} }{ -1 } = - \frac{a}{b} $$
Esempio. Il quoziente tra 1/2 e -1 è uguale a -1/2 $$ \frac{1}{2} : (-1) = \frac{1}{2} : ( \frac{-1}{1} ) = \frac{1}{2} \cdot ( \frac{-1}{1} ) = \frac{1 \cdot (-1)}{2 \cdot 1} = - \frac{1}{2} $$ Dove -1/2 è l'opposto di 1/2 perché la loro somma è uguale a zero $$ \frac{1}{2} + ( - \frac{1}{2} ) = \frac{1}{2} - \frac{1}{2} = 0 $$
Il quoziente di due numeri razionali non è detto che sia minore o uguale al dividendo. Può anche essere maggiore del dividendo.
Esempio. Il quoziente tra 5 e 1/2 è uguale a 10 ed è un numero maggiore rispetto al dividendo (5) $$ 5 : \frac{1}{2} = \frac{5}{1} : \frac{1}{2} = \frac{5}{1} \cdot \frac{2}{1} = \frac{5 \cdot 2}{1 \cdot 1} = \frac{10}{1} = 10 $$
Potenza
La potenza ennesima di un numero razionale è uguale alla potenza ennesima del numeratore fratto la potenza ennesima del denominatore $$ (\frac{a}{b})^n = \frac{a^n}{b^n} $$
Anche per quanto riguarda i numeri razionali la potenza può essere vista come la moltiplicazione di un numero per se stesso ripetuta più volte.
Esempio. La frazione 2/5 elevata alla terza è uguale alla frazione 2^3/5^3 $$ (\frac{2}{5})^3 = \frac{2}{5} \cdot \frac{2}{5} \cdot \frac{2}{5} = \frac{2 \cdot 2 \cdot 2}{5 \cdot 5 \cdot 5} = \frac{2^3}{5^3}$$
Per quanto riguarda il segno vale la regola della moltiplicazione
Pertanto, il segno della potenza dipende se l’esponente è numero intero pari o dispari
- Se l’esponente è pari, la potenza di un numero razionale non nullo ha sempre il segno positivo.
- Se l’esponente è dispari, la potenza ha segno più se il numero razionale è positivo, ha segno meno se il numero razionale è negativo.
Esempio. La potenza del numero razionale 2/5 al quadrato o al cubo ha sempre segno più (+) perché la moltiplicazione si ripete su un numero razionale positivo. $$ ( \frac{2}{5})^2 = \frac{2}{5} \cdot \frac{2}{5} = \frac{4}{25} $$ $$ ( \frac{2}{5})^3 = \frac{2}{5} \cdot \frac{2}{5} \cdot \frac{2}{5} = \frac{8}{125} $$ La potenza del numero razionale -2/5 al quadrato ha segno più (+) perché la moltiplicazione si ripete un numero pari di volte su un numero razionale negativo. $$ ( - \frac{2}{5})^2 = (- \frac{2}{5} ) \cdot (- \frac{2}{5} ) = \frac{4}{25} $$ Viceversa, la potenza del numero razionale -2/5 al cubo ha segno meno (-) perché la moltiplicazione del numero negativo per se stesso si ripete un numero dispari di volte. $$ ( - \frac{2}{5})^3 = ( - \frac{2}{5} ) \cdot (- \frac{2}{5} ) \cdot (- \frac{2}{5} ) = - \frac{8}{125} $$
La potenza di un numero razionale diverso da zero con esponente negativo è una potenza che ha per base il reciproco del numero razionale e per esponente il numero opposto dell’esponente.
$$ (\frac{a}{b})^{-n} = (\frac{b}{a})^{n}$$
E così via
