Esercizio

Trovare la retta tangente al grafico della funzione f(x) che sia parallela alla retta y=x $$ f(x) = \sqrt(x) $$

Ecco la rappresentazione grafica della funzione (verde) e della retta (nera).

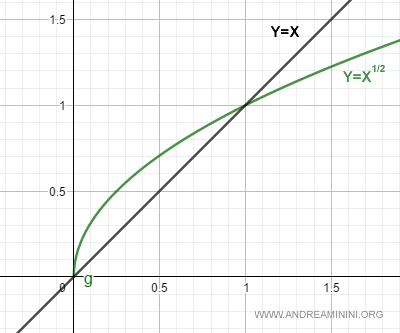
Il coefficiente angolare della funzione f(x) è uguale alla derivata f'(x) e varia da punto a punto.

Quindi, calcolo la derivata prima della funzione

$$ f'(x) = \frac{1}{2 \cdot \sqrt{x}} $$

Il coefficiente angolare m della retta y = x è invece costante ed è uguale a 1.

$$ y = m \cdot x $$

$$ y = 1 \cdot x $$

Ora devo trovare il punto della funzione in cui l'inclinazione è uguale alla retta, ossia a 1.

$$ f'(x) = 1 $$

ossia

$$ f'(x) = \frac{1}{2 \cdot \sqrt{x}} = 1 $$

Risolvo l'equazione per x

$$ \frac{1}{2 \cdot \sqrt{x}} = 1 $$

$$ \sqrt{x} = \frac{1}{2} $$

$$ x = \frac{1}{4} $$

Una volta trovata la x, calcolo il valore della funzione y=f(x) nel punto x=1/4.

$$ f(\frac{1}{4}) = \sqrt{ \frac{1}{4} } = \frac{1}{2} $$

Ho trovato le coordinate del punto di tangenza.

$$ P = \begin{pmatrix} \frac{1}{4} \\ \frac{1}{2} \end{pmatrix} $$

Ecco la rappresentazione grafica.

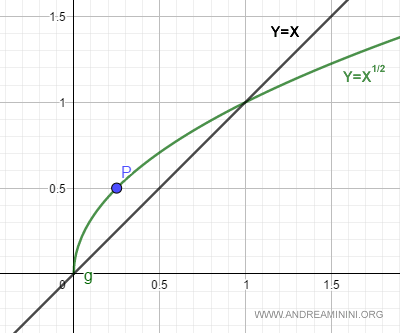
A questo punto ho le coordinate del punto della funzione con la retta tangente parallela a y=x.

Per trovare l'equazione della retta tangente applico la formula

$$ y - y_0 = m ( x - x_0 ) $$

Sostituisco le coordinate (x₀,y₀) del punto P.

$$ y - \frac{1}{2} = m \cdot ( x - \frac{1}{4} ) $$

La retta deve essere parallela alla retta y=x, quindi deve avere lo stesso coefficiente angolare m=1.

$$ y - \frac{1}{2} = 1 \cdot ( x - \frac{1}{4} ) $$

Con pochi passaggi algebrici ottengo l'equazione della retta tangente nel punto P

$$ y = x + \frac{1}{4} $$

Per finire la rappresento sul diagramma cartesiano.

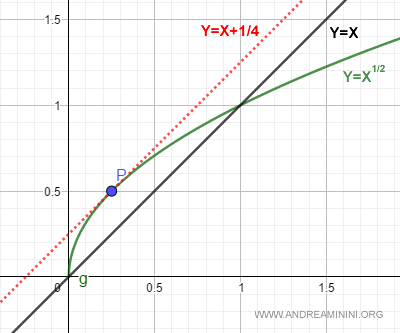
Ho così trovato la retta tangente (rossa) alla funzione f(x) parallela alla retta y=x (nera).

E così via.