Calcolo della radice quadrata in modo iterativo
Questo algoritmo calcola una stima approssimativa della radice quadrata di un numero N tramite una funzione di trasformazione g(x), una stima iniziale x0 e un ciclo di iterazioni. $$ x_{n+1} = \frac{1}{2} \cdot ( x_n + \frac{N}{x_n} ) $$
L'algoritmo converge alla radice quadrata del numero N in modo quadratico.
Il computo termina quando il valore assoluto della differenza tra due stime successive è inferiore a una soglia che considero accettabile.
Ad esempio, 0,1 o altro.
$$ | x_{n+1} - x_n | < 0,1 $$
La soglia di accettazione determina l'accuratezza della stima e il numero di iterazioni.
Quanto più è bassa la soglia di accettazione, tanto più è accurata la stima e tante più iterazioni sono necessarie per ottenerla.
Nota. L'algoritmo che ho descritto è anche noto come "metodo babilonese" o "metodo di Erone". Erone di Alessandria era un matematico greco antico che ha descritto questo metodo nei suoi scritti, ma è noto che era utilizzato anche dai babilonesi molto tempo prima di lui.
Un esempio pratico
Considero il numero N=81
$$ 81 $$
Calcolo la stima della radice quadrata di 81 in modo iterativo
$$ \sqrt{81} $$
Fisso come soglia accettabile 0,1
$$ | x_{n+1} - x_n | < 0,1 $$
Scelgo come prima stima iniziale x0=1
$$ x_0 = 1 $$
Il valore iniziale x0 è a libera scelta. Qualsiasi valore va bene.
Nota. Tuttavia, dovendo scegliere un numero a caso è utile utilizzare la metà del radicando ossia x0=N/2 se N è pari oppure x0=(N+1)/2 se N è dispari. Spesso, questo fa risparmiare almeno un passaggio rispetto a x0=1.
A questo punto comincia il calcolo iterativo.
Iterazione 1
Calcolo la stima successiva x1 utilizzando la funzione di trasformazione g(x)
$$ x_1 = \frac{1}{2} \cdot ( x_0 + \frac{N}{x_0} ) $$
Dove N=81 e x0=1
$$ x_1 = \frac{1}{2} \cdot ( 1 + \frac{81}{1} ) $$
$$ x_1 = \frac{1}{2} \cdot 82 $$
$$ x_1 = 42 $$
La prima iterazione termina con una stima x1=42
La differenza rispetto alla stima iniziale x0=1 è ancora troppo grande
$$ | 42 - 1 | = 41 > 0,1 $$
Quindi, procedo con la seconda iterazione.
Iterazione 2
Nella seconda iterazione calcolo x2 a partire da x1=41
$$ x_2 = \frac{1}{2} \cdot ( x_1 + \frac{N}{x_1} ) $$
$$ x_2 = \frac{1}{2} \cdot ( 41 + \frac{81}{41} ) $$
$$ x_2 = 21,4878 $$
La differenza rispetto alla stima precedente x1=41 è ancora troppo grande.
$$ | 21,4878 - 41 | = 19.5122 > 0,1 $$
Quindi, procedo con la terza iterazione.
Iterazione 3
Questa volta calcolo x3 a partire da x2=21,4878
$$ x_3 = \frac{1}{2} \cdot ( x_2 + \frac{N}{x_2} ) $$
$$ x_3 = \frac{1}{2} \cdot ( 21,4878 + \frac{81}{21,4878} ) $$
$$ x_3 = 12,6287 $$
La differenza rispetto alla stima precedente x2=21,4878 si riduce ma è ancora grandeo.
$$ | 12,6287 - 21,4878 | = 8,8591 > 0,1 $$
Quindi, procedo con la quarta iterazione.
Iterazione 4
Nella quarta iterazione calcolo x4 a partire da x3=12,6287
$$ x_4 = \frac{1}{2} \cdot ( x_3 + \frac{N}{x_3} ) $$
$$ x_4 = \frac{1}{2} \cdot ( 12,6287 + \frac{81}{12,6287} ) $$
$$ x_4 = 9,5213 $$
La differenza rispetto alla stima precedente x3=12,6287 si riduce ulteriormente ma è ancora grande.
$$ | 9,5213 - 12,6287 | = 3.1074 > 0,1 $$
Quindi, procedo con la quinta iterazione.
Iterazione 5
Calcolo la stima x5 a partire da x4=9,5213
$$ x_5 = \frac{1}{2} \cdot ( x_4 + \frac{N}{x_4} ) $$
$$ x_5 = \frac{1}{2} \cdot ( 9,5213 + \frac{81}{9,5213} ) $$
$$ x_5 = 9,0143 $$
La differenza assoluta rispetto alla stima precedente x4=9,5213 è ancora troppo grande
$$ | 9,0143-9,513| = 0,4987 > 0,1 $$
Quindi procedo con la sesta iterazione.
Iterazione 6
Calcolo x6 a partire da x5=9,0143
$$ x_6 = \frac{1}{2} \cdot ( x_5 + \frac{N}{x_5} ) $$
$$ x_6 = \frac{1}{2} \cdot ( 9,0143 + \frac{81}{9,0143} ) $$
$$ x_6 = 9,000011 $$
Ora la differenza tra le stime x6 e x5 è sufficientemente piccola.
E' inferiore alla soglia di accettazione che ho fissato a 0,1
$$ | 9,000011 - 9,0143 | = 0,014 < 0,1 $$
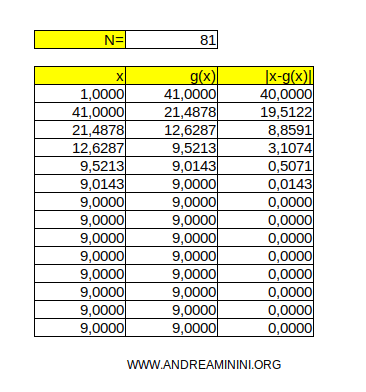
L'algoritmo termina qui. L'ultimo valore trovato x6=9,000011 è il valore approssimato della radice quadrata di 81.
Nota. Riducendo ulteriormente la soglia di accettazione posso trovare un valore approssimato più accurato, al costo di compiere ulteriori iterazioni.
Calcolo della radice ennesima approssimata
Per calcolare una radice ennesima $ \sqrt[n]{A} $ si può usare il metodo di Newton generalizzato. \[ x_{k+1} = \frac{1}{n} \cdot \left( (n-1) \cdot x_k + \frac{A}{x_k^{n-1}} \right) \]
Dove:
- \( x_k \) è l’approssimazione corrente
- \( x_{k+1} \) è l’approssimazione successiva
- \( A \) è il numero di cui vuoi calcolare la radice n-esima
- \( n \) è l’indice della radice
Anche in questo caso il primo valore $ x_0 $ è una stima a propria scelta.
Nota. Con $ n=2 $ ottengo la formula per calcolare la radice quadrata. \[ x_{k+1} = \frac{1}{2} \cdot \left( (2-1) \cdot x_k + \frac{A}{x_k^{2-1}} \right) \] \[ x_{k+1} = \frac{1}{2} \cdot \left( x_k + \frac{A}{x_k} \right) \]
Esempio
Provo a calcolare la radice cubica di 27
$$ \sqrt[3]{27} $$
Utilizzo la formula per \( n = 3 \):
\[ x_{k+1} = \frac{1}{3} \left( 2x_k + \frac{27}{x_k^2} \right) \]
Inizio con \( x_0 = 1 \) ma qualsiasi altro numero sarebbe andato bene, tranne \( x_0 = 0 \) che causa una divisione per zero.
Fisso come soglia accettabile \( S=0,01 \)
Iterazione 1:
\[ x_1 = \frac{1}{3} \left(2 \cdot 1 + \frac{27}{1^2} \right) = \frac{1}{3}(2 + 27) = \frac{29}{3} \approx 9.6667 \]
\[ S_1 = | x_1 - x_0 | = |9.6667 - 1 | = 8.6667 \]
Iterazione 2:
\[ x_2 = \frac{1}{3} \left(2 \cdot 9.6667 + \frac{27}{9.6667^2} \right) \approx 6.5408 \]
\[ S_2 = | x_2 - x_1| = |6.5408 - 9.6667 | = 3.1259 \]
Iterazione 3:
\[ x_3 = \frac{1}{3} \left(2 \cdot 6.5408 + \frac{27}{6.5408^2} \right) \approx 4.570877 \]
\[ S_3 = |x_3 - x_2| = |4.570877 - 6.5408| = 1.9698 \]
Iterazione 4:
\[ x_4 = \frac{1}{3} \left(2 \cdot 4.5709 + \frac{27}{4.5709^2} \right) \approx 3.478019 \]
\[ S_4 = |x_4 - x_3| = | 3.478019 - 4.570877| = 1.0928 \]
Iterazione 5:
\[ x_5 = \frac{1}{3} \left(2 \cdot 3.478019 + \frac{27}{3.478019^2} \right) \approx 3.062689 \]
\[ S_5 = |x_5 - x_4| = | 3.062689 - 3.478019| = 0.4153 \]
Iterazione 6:
\[ x_6 = \frac{1}{3} \left(2 \cdot 3.062689 + \frac{27}{3.062689^2} \right) \approx 3.001274 \]
\[ S_6 = |x_6 - x_5| = | 3.001274 - 3.062689 | = 0.0614 \]
Iterazione 7:
\[ x_7 = \frac{1}{3} \left(2 \cdot 3.001274 + \frac{27}{3.001274^2} \right) \approx 3.000001 \]
\[ S_7 = |x_7 - x_6| = | 3.000001 - 3.001274 | = 0.0012 \]
In quest'ultimo caso la soglia di accettazione è soddisfatta, perché la differenza $ S_7= 0.0012 $ è minore rispetto alla soglia che ho fissato inizialmente $ S=0.01 $. L'algoritmo può interrompersi qui.
$$ S_7 = 0.0012 < S=0.01 $$
Quindi, dopo 7 iterazioni, ottengo un risultato accettabile \( x \approx 3.000001 \)
$$ \sqrt[3]{27} \approx 3.000001 $$
In conclusione, il metodo converge bene e la precisione aumenta rapidamente.
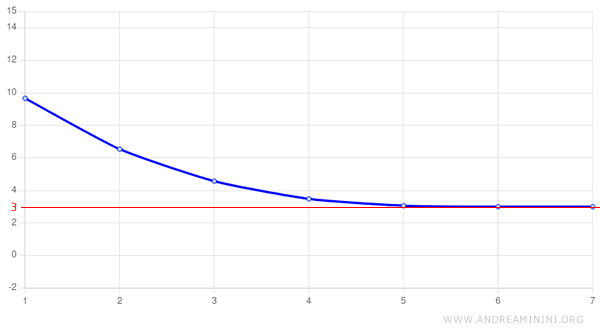
Nota. La radice cubica di 27 è 3, quindi l'algoritmo è giunto a una soluzione approssimata molto vicina a quella effettiva. La precisione aumenta con il numero delle iterazioni. Quindi, è molto importante fissare all'inizio del procedimento una soglia di accettazione \( S \) del tipo: $$ | x_k - x_{k-1} | < S $$ Questo sia per ottenere un risultato accettabile, sia per evitare di effettuare troppe iterazioni.
Note aggiuntive
Alcune osservazioni sull'algoritmo
- La stima iniziale x0 è a libera scelta. Qualsiasi valore va bene. Ad esempio, avrei potuto scegliere x0=1000 o x0=9999. In ogni caso l'algoritmo converge verso la stima della radice quadrata di N=81. Ovviamente, cambia il numero delle iterazioni necessarie per raggiungerla.
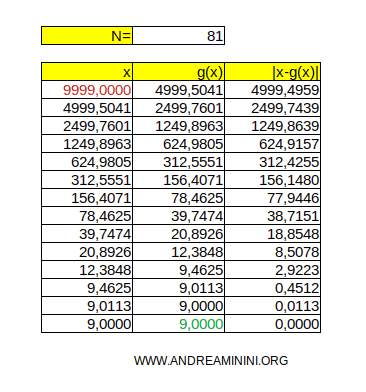
- Dovendo scegliere un numero a caso è utile utilizzare la metà del radicando ossia x0=N/2 se N è pari oppure x0=(N+1)/2 se è dispari.
- L'algoritmo calcola una stima della radice quadrata di qualsiasi numero. Ad esempio, se scelgo N=15129, l'algoritmo restituisce la sua radice quadrata, ossia 123, in dieci iterazioni.
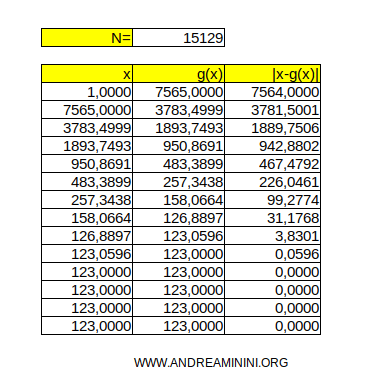
E così via.
