Il metodo di bisezione
il metodo di bisezione (o metodo della ricerca degli zeri) è una tecnica numerica per trovare le radici di una funzione continua in un intervallo \([a, b]\), dove la funzione cambia segno.
In altre parole, trova un punto \( p \) tale che \( f(p) = 0 \), cioè uno zero della funzione \( f(x) \), sapendo che c'è almeno una radice nell'intervallo \([a, b]\)
$$ f(a) \cdot f(b) < 0 $$
Inoltre, la funzione \( f \) è continua nell'intervallo \([a, b] \).
Come funziona il metodo
- Si calcola il punto medio \( p = \frac{a + b}{2} \)
- Si valuta \( f(p) \)
- A seconda del segno di \( f(p) \), si sostituisce \( a \) o \( b \) per restringere l'intervallo contenente la radice
- Si ripete il processo (iterazioni) fino a soddisfare una condizione di arresto, come:
- Errore assoluto \( |p_n - p_{n-1}| < \varepsilon \)
- Errore relativo \( \frac{|p_n - p_{n-1}|}{|p_n|} < \varepsilon \)
- Valore piccolo della funzione \( |f(p_n)| < \varepsilon \)
Questo metodo è semplice da implementare e robusto, perché converge sempre se \( f(a) \cdot f(b) < 0 \).
D'altra parte, è un processo lento e richiede molte iterazioni per una buona precisione.
In più richiede che \( f(a) \) e \( f(b) \) abbiano segni opposti e può scartare approssimazioni migliori.
Nota. Il metodo di bisezione è un ottimo punto di partenza per trovare zeri, soprattutto quando non si ha un’ottima approssimazione iniziale. Tuttavia, per efficienza e velocità, è spesso affiancato o sostituito da metodi più rapidi come Newton-Raphson o il metodo della secante.
Un esempio pratico
Ecco un esempio passo-passo del metodo di bisezione applicato a una funzione.
Devo trovare una radice di \( f(x) = \cos(x) - x \) nell'intervallo \([0, 1]\).
Per prima cosa calcolo e verifico se la funzione ha segno opposto agli estremi dell'intervallo.
$$ f(0) = \cos(0) - 0 = 1 $$
$$ f(1) = \cos(1) - 1 \approx 0.5403 - 1 = -0.4597 $$
Poiché ha segno opposto \( f(0) \cdot f(1) < 0 \), deduco che esiste almeno una radice in \([0, 1]\)
Fisso una precisione di 3 cifre decimali: usando una tolleranza \( \text{TOL} = 0.001 \).
Ecco le prime iterazioni:
| n | a | b | p = (a + b)/2 | f(p) = cos(x)-x | Intervallo scelto |
|---|---|---|---|---|---|
| 1 | 0.000 | 1.000 | 0.500 | cos(0.5) - 0.5 ≈ 0.3776 | f(p) > 0 ⇒ [0.5, 1] |
| 2 | 0.500 | 1.000 | 0.750 | cos(0.75) - 0.75 ≈ -0.0183 | f(p) < 0 ⇒ [0.5, 0.75] |
| 3 | 0.500 | 0.750 | 0.625 | cos(0.625) - 0.625 ≈ 0.1850 | f(p) > 0 ⇒ [0.625, 0.75] |
| 4 | 0.625 | 0.750 | 0.6875 | cos(0.6875) - 0.6875 ≈ 0.0844 | [0.6875, 0.75] |
| 5 | 0.6875 | 0.750 | 0.71875 | cos(0.71875) - 0.71875 ≈ 0.0333 | [0.71875, 0.75] |
| 6 | 0.71875 | 0.750 | 0.734375 | cos(0.734375) - 0.734375 ≈ 0.0073 | [0.734375, 0.75] |
| 7 | 0.734375 | 0.750 | 0.7421875 | cos(0.7421875) - 0.7421875 ≈ -0.0055 | [0.734375, 0.7421875] |
| 8 | 0.734375 | 0.7421875 | 0.73828125 | cos(0.73828125) - 0.73828125 ≈ 0.0009 ✅ | Stop! |
Spiegazione. Nella prima iterazione \( n =1 \) il punto medio dell'intervallo è \( p = 0.5 \) e il valore della funzione in questo punto è $ f(0.5) = \cos(0.5) - 0.5 = 0.3776 $. Poiché è un valore positivo, deduco che la radice, ossia il punto in cui la funzione è nulla e cambia di segno, si trova più a destra rispetto a 0.5, quindi riduco l'intervallo da \( [0,1] \) a \( [0.5,1] \) e procedo con la seconda iterazione. Nella seconda iterazione \( n=2 \) il punto medio dell'intervallo è \( p = 0.750 \) in cui la funzione ha un valore negativo \( f(0.75) = -0.0183 \). In questo caso, deduco che la radice si trovi a sinistra di 0.75. Quindi riduco l'intervallo da \( [0.5,1] \) a \( [0.5,0.75] \) e procedo con la terza iterazione. Il processo continua finché non trovo un punto \( p \) in cui la funzione \( f(p) = 0 \pm 0.001 \) sia vicina a zero con un margine di tolleranza di ±0.001.
Dopo 8 iterazioni, trovo che un risultato vicino allo zero con una precisione inferiore a 0.001:
\[ p \approx 0.73828125 \quad \text{con } |f(p)| < 0.001 \]
Quindi la radice di \( \cos(x) = x \) è approssimativamente 0.738, che è corretta a 3 cifre decimali.
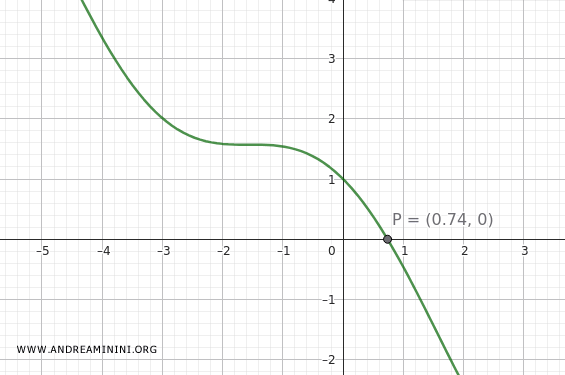
Ma funziona sempre? Il metodo di bisezione funziona, ma solo se la funzione cambia segno nell’intervallo, come in questo esempio, ed è una funzione continua (senza buchi). Se in un intervallo si verifica \( f(a) \cdot f(b) > 0 \), questo metodo non trova la radice nemmeno se c'è veramente. Inoltre, è un metodo molto lento. Un altro limite è che bisogna individuare gli intervalli in cui si trovano le radici di una funzione e non sempre è facile trovarli a priori. E' un po' come cercare le chiavi perse in salotto… è facile solo se sai già che stanno da qualche parte tra il divano e la finestra.
Esplorazione del dominio: come individuare gli intervalli contenenti radici
L'esplorazione del dominio di una funzione consiste nel trovare gli intervalli \([a, b]\) dove \( f(a) \cdot f(b) < 0 \), cioè la funzione cambia segno e quindi c'è una radice lì dentro.
E' il passo preliminare fondamentale per individuare gli intervalli in cui applicare il metodo di bisezione.
In pratica, consiste nel valutare la funzione in una sequenza di punti distribuiti nel dominio e cercare coppie di punti consecutivi \( a \) e \( b \) in cui la funzione cambi segno, ossia \( f(a) \cdot f(b) < 0 \).
Per il teorema degli zeri, in questi intervalli \([a, b]\) deve esistere almeno una radice nell’intervallo.
La scelta della distanza tra i punti, detta passo di esplorazione, ed è cruciale perché:
- se troppo grande, rischia di saltare cambi di segno e quindi perdere radici
- se troppo piccolo, garantisce l’individuazione di tutte le radici ma aumenta notevolmente il costo computazionale
Per questo, si cerca un compromesso tra accuratezza ed efficienza, adottando un passo abbastanza fine da catturare i comportamenti significativi della funzione, ma non tanto minuto da rendere l'esplorazione inutilmente pesante.
Solo dopo aver identificato con successo gli intervalli con cambio di segno, si procede ad applicare il metodo di bisezione in ciascuno di essi.
Esempio
Devo trovare tutte le radici reali della funzione
\[ f(x) = x^3 - 2x^2 - x + 1 \]
Inizialmente non so in quale intervallo cercare. Essendo un polinomio di terzo grado, posso dedurre che può avere fino a tre radici reali ma non so dove sono le radici, quante sono e se ci sono.
Non posso nemmeno trovarle a occhio, perché non ci sono numeri interi evidenti, quindi serve un’esplorazione numerica.
Provo ad analizzare la funzione in alcuni punti con un passo di esplorazione pari a 5
\[
\begin{array}{c|c}
x & f(x) \\
\hline
-10 & -1189 \\
-5 & -169 \\
0 & 1 \\
5 & 71 \\
10 & 791 \\
\end{array}
\]
Dalla tabella mi accorgo che deve esserci almeno una radice nell'intervallo (-5,0).
Tuttavia, se mi basassi solo su questa analisi farei un errore perché il passo di esplorazione è troppo grande. Sto sorvolando la funzione da troppo in alto.
Ad esempio, riduco il passo di esplorazione a 1 per scendere più nel dettaglio.
\[
\begin{array}{cc}
x & f(x) \\
\hline
-5 & -169 \\
-4 & -91 \\
-3 & -41 \\
-2 & -13 \\
-1 & -1 \\
0 & 1 \\
1 & -1 \\
2 & -1 \\
3 & 7 \\
4 & 29 \\
5 & 71 \\
\end{array}
\]
Così facendo mi accorgo che nella funzione c'è un primo cambio di segno nell'intervallo (-1,0), un secondo cambio di segno nell'intervallo (0,1) e un terzo cambio di segno nell'intervallo (2,3)
Nota. Questo dimostra che se esploro con balzi troppo grandi, potrei saltare radici tra due valori. Se, invece, esploro con balzi troppo piccoli, trovo tutto ma il costo computazionale aumenta inutilmente. Ad esempio, un passo 0.1 nell'intervallo \([-10, 10]\) implica 200 valutazioni ed è troppo costoso. Come sempre, ... in medio stat virtus. Serve un compromesso intelligente, ad esempio usare un passo di 0.5 o 0.25, a seconda della funzione.
Una volta individuati gli intervalli posso applicare il metodo di bisezione su ciascuno di essi
- Primo intervallo: \([-1, 0]\)
In poche interazioni giungo a una radice approssimata: \[ x_1 \approx -0.8 \] - Secondo intervallo: \([0, 1]\)
Anche in questo caso non occorrono molte iterazioni per arrivare a una radice approssimata \[ x_2 \approx 0.5 \] - Terzo intervallo: \([2, 3]\)
Applico nuovamente il metodo di bisezione in questo intervallo e trovo la terza radice \[ x_3 \approx 2.2 \]
Pertanto, le tre radici approssimate della funzione \( f(x) = x^3 - 2x^2 - x + 1 \) sono \( x_1 \approx -0.8 \) , \( x_2 \approx 0.5, \) e \( x_3 \approx 2.2 \).
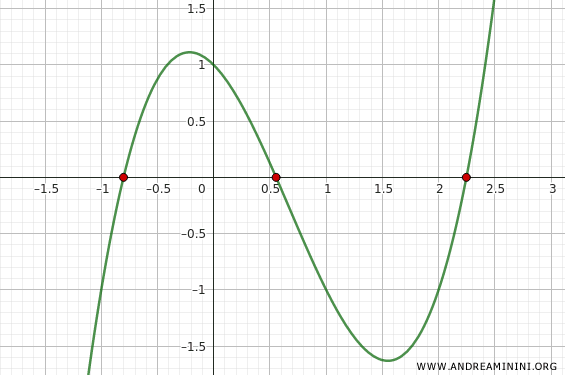
In conclusione esplorare il dominio è essenziale per localizzare gli intervalli delle radici prima di usare il metodo di bisezione.
Serve un passo bilanciato, né troppo grande, né troppo piccolo.
Una volta trovati gli intervalli con cambio di segno, si applica il metodo di bisezione localmente, in modo efficiente e sicuro
E così via.
