Metodo iterativo per trovare lo zero di una funzione

Per trovare lo zero di una funzione posso anche utilizzare un metodo iterativo.

Cos'è lo zero di una funzione? Lo zero di una funzione è il punto in cui la funzione interseca l'asse delle x. In altre parole, è il valore di x per cui la funzione f(x) = 0. $$ f(x)=0 $$

Trasformo il problema in una ricerca di punto fisso di una trasformazione g(x).

$$ g(α)=α $$

Cos'è un punto fisso? Un punto fisso di una funzione g(x) è un numero α tale che g(α) = α. In altre parole, è un valore che rimane invariato quando applichiamo la funzione.

La funzione g(x) è una funzione di trasformazione della funzione iniziale. Ad esempio

$$ g(x) = x + k \cdot f(x) $$

Dove k è un numero reale qualsiasi che identifica la costante di contrazione.

Nota. La funzione di trasformazione g(x) può anche essere diversa dalla precedente. La scelta della funzione g(x) è di fondamentale importanza per la risoluzione di un problema in modo iterativo. Deve essere efficace, veloce e non troppo costosa in termini di operazioni di calcolo.

Ora il problema è trovare un valore α tale che g(α)=α

Per trovarlo assegno un valore iniziale x=x₀, calcolo il risultato g(x₀) e lo assegno a x₁.

$$ x_1 = g(x_0) $$

Il procedimento continua in modo iterativo

$$ x_{n+1} = g(x_n) $$

Come condizione di uscita dalle iterazioni imposto una differenza di 0,1 tra il valore x_n+1 e quello precedente x_n

$$ |x_{n+1} - x_n | < 0,1 $$

Dopo un tot numero di iterazioni, il metodo dovrebbe convergere alla soluzione del problema, purché siano soddisfatte queste condizioni

1. La funzione f(x) deve essere derivabile
2. La successione di termini x₀, x₁, x₂, ... deve convergere al punto α
3. La convergenza deve essere veloce per ridurre i costi computazionali
4. La costante di contrazione (k) deve essere piccola.

   Nota. La costante di contrazione influisce sia sull'efficacia che sulla velocità. Se k è grande, la ricerca smette di convergere. Se k è troppo piccola, la convergenza diventa più lenta. Quindi, la difficoltà sta nel trovare un valore di k abbastanza basso ma non troppo. Per un approfondimento ho scritto delle osservazioni a proposito in fondo a questa pagina.

E' comunque buona norma fissare anche un numero massimo di iterazioni come condizione di uscita forzata. Ad esempio n=1000.

In questo modo evito il rischio di un loop infinito o un eccessivo consumo di risorse computazionali.

Un esempio pratico

Considero la funzione f(x)

$$ f(x) = x^2 - 16 $$

Devo trovare gli zeri della funzione.

Nota. Ho scelto una funzione banale per poter spiegare meglio il procedimento. E' evidente a colpo d'occhio che la soluzione è x= ±4.

Utilizzo questa funzione di trasformazione g(x).

$$ g(x) = x + k \cdot f(x) $$

In questo caso, sapendo che f(x)=x²-16 la funzione di trasformazione g(x) diventa

$$ g(x) = x + k \cdot (x^2-16) $$

Scelgo come costante di contrazione k=0,12

$$ g(x) = x + 0,12 \cdot (x^2-16) $$

Ora il problema consiste nel trovare un punto fisso ossia un valore x=α tale che g(α)=α

Nota. Dal punto di vista geometrico questa condizione si verifica quando la retta y=x interseca la funzione g(x). Come si può vedere, l'intersezione avviene in x=4 e x=-4.

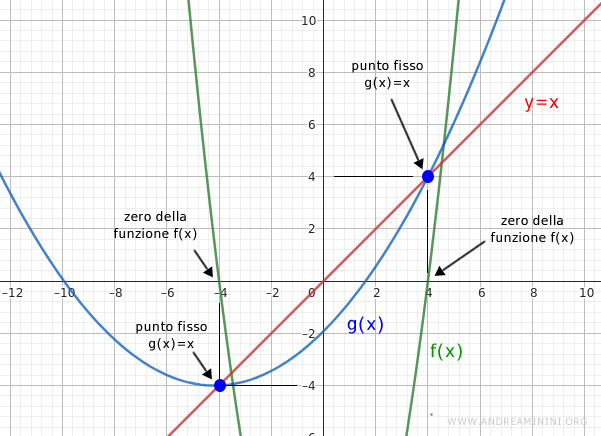
Scelgo un valore iniziale della x a caso.

Ad esempio x₀=0

$$ x_0 = 0 $$

A questo punto calcolo x₁ utilizzando la funzione di trasformazione

$$ x_1 = g(x_0) = x_0 + 0,12 \cdot (x_0^2-16) $$

$$ x_1 = g(0) = 0 + 0,12 \cdot (0^2-16) $$

$$ x_1 = g(0) = 0,12 \cdot (-16) $$

$$ x_1 = -1,92 $$

Una volta trovato x₁=-1,92, reitero il processo calcolando x₂=g(x₁)

$$ x_2 = g(x_1) = x_1 + 0,12 \cdot (x_1^2-16) $$

$$ x_2 = g(x_1) = (-1,92) + 0,12 \cdot ((-1,92)^2-16) $$

$$ x_2 = g(x_1) = - 3,397632 $$

Una volta trovato x₂=-3,397632, reitero il processo per calcolare x₃=g(x₂)

$$ x_3 = g(x_2) = x_2 + 0,12 \cdot (x_2^2-16) $$

$$ x_3 = g(x_2) = -3,932363 $$

Man mano che effettuo una nuova iterazione i valori di x_n convergono a -4.

Una volta trovato x₃=-3,932363, reitero il processo per calcolare x₄=g(x₃)

$$ x_4 = g(x_3) = x_3 + 0,12 \cdot (x_3^2-16) $$

$$ x_4 = g(x_3) = -3,996745 $$

L'iterazione termina qui perché la differenza assoluta tra i due valori |x₄-x₃|<0,1 è minore della soglia della condizione accettabile di uscita (0,1)

$$ |x_4 - x_3| = |-3,996745-(3,932363)| = 0.064382 < 0,1 $$

In conclusione, la soluzione approssimativa del problema è x=-3,996745

In questo caso l'algoritmo ha impiegato 4 iterazioni per trovare la soluzione appossimata.

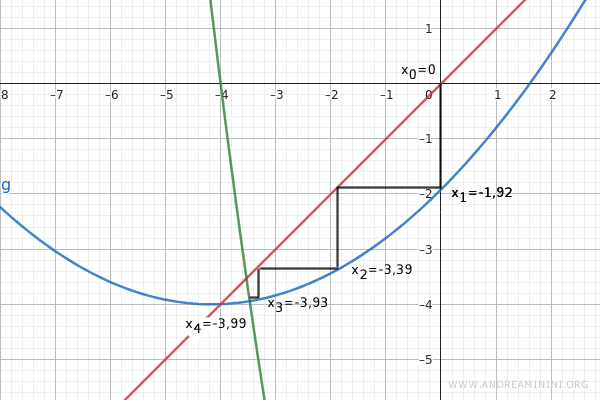
Nota. Ovviamente, abbassando ulteriormente la soglia di accettazione da 0,12 a 0,001 la stima sarebbe stata più vicina a -4, a costo però di ulteriori iterazioni dell'algoritmo. In questo caso comporterebbe solo due iterazione in più... ma il problema analizzato nell'esempio è volutamente banale.

Osservazioni

L'esempio precedente è utile per sottolineare alcune problematiche interessanti.

1. Scegliendo la costante di contrazione k=0,12 l'algoritmo ha impiegato 4 iterazioni per giungere a un risultato accettabile. Tuttavia, in altri casi il risultato sarebbe stato ben diverso.
   
   Ad esempio, con la costante di contrazione k=0,05 la successione converge molto più lentamente verso la soluzione.
   
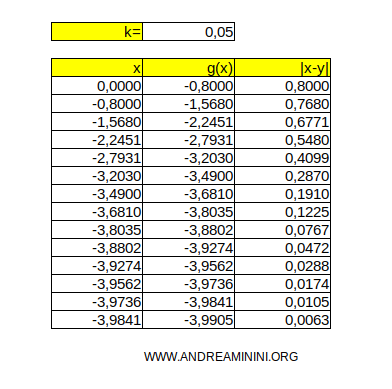
   Con la costante di contrazione k=0,4 invece la successione diverge e l'algoritmo non trova alcuna soluzione.
   
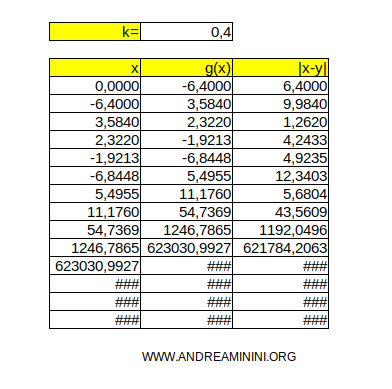
   Pertanto, la funzione di trasformazione g(x) utilizzata nell'esempio è molto instabile. Esistono altre funzioni di trasformazione più complesse ma anche più stabili ed efficaci.

E così via.