Le congruenze nell'aritmetica modulare

Dati due interi a,b con b>0 si dicono congrui modulo $ n $ se la loro differenza $ a-b $ è divisibile per un intero $ n >0 $ $$ a \equiv b \mod n $$

In alternativa

Dati due numeri interi a e b>0 si dicono congrui modulo $ n>0 $ se hanno lo stesso resto nella divisione intera per $ n $. $$ a \equiv b \mod n $$

In altre parole, una congruenza modulo \( n \) indica che due numeri, \( a \) e \( b \), lasciano lo stesso resto quando vengono divisi per \( n \).

Queste due condizioni sono equivalenti. Se una è vera, lo sarà automaticamente anche l’altra.

Nella teoria dei numeri le congruenze estendono il concetto di uguaglianza tra numeri interi.

A differenza dell’uguaglianza tradizionale, le congruenze tengono conto del comportamento dei numeri rispetto alla divisione per un valore fisso, noto come modulo.

Esempio. Dati tre numeri interi \( a=17 \), \( b=5 \), e \( n=6 \) (con \( n > 0 \)), si dice che \( a \) è congruente a \( b \) modulo \( n \) – e si scrive $ a \equiv b \pmod{n} $ se, e solo se, la differenza \( a - b \) è un multiplo di \( n \). In altre parole, se esiste un intero \( k \) tale che \( a - b = kn \). Per verificare la congruenza, calcolo la differenza $ a-b $: $$ 17 - 5 = 12 $$ Poiché \( 12 \) è un multiplo di \( n=6 \), in quanto \( 12 = 2 \cdot 6 \), posso concludere che 17 e 5 sono numeri interi congruenti modulo 6. $$ 17 \equiv 5 \pmod{6} $$ Questo vuol dire che dividendo sia \( 17 \) che \( 5 \) per \( 6 \), il resto $ r $ in entrambi i casi è lo stesso. $$ 17 \div 6 = 2 \ \ r=5 $$ $$ 5 \div 6 = 0 \ \ r=5 $$

Quindi, la congruenza è una relazione di equivalenza tra numeri interi Z con i multipli di un numero intero positivo n.

$$ a \: p_n \: b \Leftrightarrow a \equiv b \mod n \Leftrightarrow a-b=n \cdot k $$

Dove k è un numero intero qualsiasi. 

Un esempio pratico

Metodo 1

Ecco un esempio di congruenza

$$ 26 \equiv 16 \mod 5 $$

Perché

$$ 26-16 = 10 $$

E il numero 10 è divisibile per 5.

Questo vuol dire che i due numeri divisi per 10 hanno lo stesso resto.

$$ \frac{26}{10} = 2 \mod 6 $$

$$ \frac{16}{10} = 1 \mod 6 $$

Metodo 2

Lo stesso esempio di congruenza dimostrato con il secondo metodo

$$ 26 \equiv 16 \mod 5 $$

Perché

$$ \frac{26}{5} = 5 \mod 1 $$

$$ \frac{16}{5} = 3 \mod 1 $$

La divisione per 5 restituisce lo stesso resto 1 con entrambi i numeri (16 e 26).

Pertanto, i numeri 16 e 26 sono congrui modulo 5.

Esempio 3

Il discorso non cambia se a<b.

Ad esempio, considero \( a = 5 \), \( b = 8 \), \( n = 6 \).

In questo caso la differenza è negativa

$$ a - b = 5 - 8 = -3 $$

Poiché \( -3 \) non è un multiplo di \( 6 \), ovvero non esiste un intero $ k $ tale che $ 6 \cdot k = -3 $, deduco che i due numeri non sono congruenti nel modulo \( 6 \).

$$ 5 \not \equiv 8 \pmod{6} $$

In alternativa, allo stesso risultato sarei potuto giungere verificando che il resto dei due numeri nella divisione per \( 6 \) è diverso.

$$  5 \div 6 = 0 + r=5 $$

$$  8 \div 6 = 1 + r=2 $$

Poiché i resti non coincidono, deduco che \( 5 \not \equiv 8 \pmod{6} \). 

A cosa servono le congruenze

Sono utili per stabilire una relazione tra l'insieme infinito dei numeri interi e un insieme finito detto insieme quoziente modulo m.

Nota. Molte discipline scientifiche ( matematica, informatica, ecc. ) usano l'insieme dei numeri interi Z. Tuttavia, non è facile lavorare con un insieme infinito. Le congruenze mi permettono di trasformarlo in un insieme finito. In questo modo tutto diventa più semplice.

Esempio

L'insieme A è composto dall'insieme dei numeri interi positivi Z+ ed è un insieme infinito.

L'insieme B è invece un insieme finito composto dai numeri 1, 2, 3

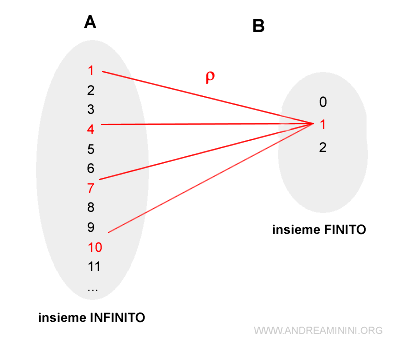
La relazione di equivalenza p mette in relazione ogni elemento di A con un elemento di B.

Il numero 4 di A è in relazione di congruenza modulo 3 con il numero 1 di B perché divisi per m=3 hanno lo stesso resto.

$$ \frac{4}{3}=1 \mod 1 $$

$$ \frac{1}{3}=0 \mod 1 $$

La stessa relazione vale per il numero 7 di A

$$ \frac{7}{3}=2 \mod 1 $$

$$ \frac{1}{3}=0 \mod 1 $$

e per il numero 10 di A

$$ \frac{10}{3}=3 \mod 1 $$

$$ \frac{1}{3}=0 \mod 1 $$

E via dicendo per tutti gli elementi (1+3n) dell'insieme A.

In conclusione, ogni numero intero dell'insieme A ha una relazione di equivalenza con un intero positivo dell'insieme B detto classe di equivalenza.

Quali sono le applicazioni pratiche? Le congruenze trovano applicazioni in molti ambiti. Ad esempio, in crittografia sono usate dal sistema RSA per cifrare i messaggi in modo sicuro. Sono utilizzate anche in algebra modulare per analizzare gli insiemi di numeri interi in cicli limitati e per risolvere problemi che coinvolgono soluzioni intere.

L'insieme quoziente modulo n

Nell'esempio precedente ho costruito una relazione di congruenza modulo 3.

Le classi di equivalenza della relazione sono :

$$ \bar{0} = \{ 3, 6, 9, 12, ... \} \\ \bar{1} = \{ 1, 4, 7, 10, ... \} \\ \bar{2} = \{ 2, 5, 8, 11, ... \} $$

L'insieme delle classi di equivalenza è detto insieme quoziente modulo n.

$$ Z_n = \{ \bar{0} , \bar{1} , \bar{2} \} $$

L'insieme quoziente modulo n è composto da n elementi a partire dallo zero.

Quindi, le classi variano da 0 a n-1.

Le operazioni sulle congruenze

Per trasformare un insieme quoziente modulo n in un anello, devo aggiungere due operazioni. $$ ( Z_n,+, \cdot ) $$

Le principali operazioni sulle congruenze sono

• Somma $$ \bar{a} + \bar{b} = \overline{a+b} $$
• Prodotto $$ \bar{a} \cdot \bar{b} = \overline{ab} $$

Esempio

La tavola dell'addizione e della moltiplicazione dell'anello (Z₆ ,+ ,·) è

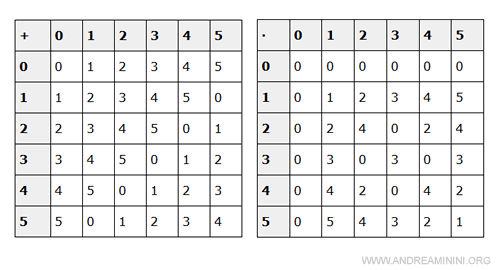
La relazione di congruenza è compatibile con entrambe le operazioni ( somma, moltiplicazione ) definite sull'insieme dei numeri interi.

In pratica, la relazione è indipendente dalla scelta dei numeri interi.

Se la relazione di congruenza è definita per

$$ a≡b \:\:(mod \: n) $$

$$ c≡d \:\:(mod \: n) $$

allora è definita anche per

$$ a+c≡b+d \:\:(mod \: n) $$

$$ ac≡bd \:\:(mod \: n) $$

Dimostrazione. Se a≡b (mod n) allora a-b=kn. Se c≡d (mod n) allora c-d=jn. Quindi, vale la somma $$ (a-b)+(c-d)=(kn+jn) $$ $$ (a+c)-(b+d)=n(k+j) $$ Pertanto, anche (a+c)≡(b+d) (mod n) sono congruenti modulo n.

Esempio

Ho due relazioni di congruenza

$$ 7 ≡ 1 \:\: (mod \: 6) \\ 8 ≡ 2 \:\: (mod \: 6) \\ $$

per la somma vale

$$ 7+8 ≡ 1+2 \:\: (mod \: 6) $$

$$ 15 ≡ 3 \:\: (mod \: 6) $$

Verifica. La divisione 15/6 ha resto 3. La divisione 3/6 ha resto 3. Pertanto, 15 e 3 sono congruenti modulo 6.

e per la moltiplicazione

$$ 7*8 ≡ 1*2 \:\: (mod \: 6) $$

$$ 56 ≡ 2 \:\: (mod \: 6) $$

Verifica. La divisione 56/6 ha resto 2. La divisione 2/6 ha resto 2. Pertanto, 56 e 2 sono congruenti modulo 6.

La divisibilità e la congruenza

Un numero a è divisibile per m soltanto se $$ a \equiv 0 \mod m $$

Esempio

Il numero 26 è divisibile per 13?

Secondo la proprietà delle congruenze

$$ 26 \equiv 0 \mod 13 $$

$$ 26 - 0 = 26 $$

e 26 è divisibile per 13.

Le proprietà delle congruenze

Le congruenze godono delle seguenti proprietà:

• Riflessività: Ogni numero è congruente a se stesso, \( a \equiv a \pmod{n} \)
• Simmetria: Se \( a \equiv b \pmod{n} \), allora \( b \equiv a \pmod{n} \)
• Transitività: Se \( a \equiv b \pmod{n} \) e \( b \equiv c \pmod{n} \), allora \( a \equiv c \pmod{n} \)
• Compatibilità con le operazioni algebriche: Se \( a \equiv b \pmod{n} \) e \( c \equiv d \pmod{n} \), allora:
  - \( a + c \equiv b + d \pmod{n} \),
  - \( a - c \equiv b - d \pmod{n} \),
  - \( ac \equiv bd \pmod{n} \).

Altre proprietà delle congruenze

Le congruenze rispettano le seguenti proprietà

• Le congruenze che hanno lo stesso modulo possono essere sommate, sottratte, moltiplicate tra loro ordinatamente i primi membri per i secondi membri. $$ a \equiv b \mod m + c \equiv d \mod m \Rightarrow a+c \equiv b+d \mod m $$ $$ a \equiv b \mod m - c \equiv d \mod m \Rightarrow a-c \equiv b-d \mod m $$ $$ a \equiv b \mod m \cdot c \equiv d \mod m \Rightarrow ac \equiv bd \mod m $$
• Una congruenza può essere moltiplicata per un numero intero k qualsiasi. $$ k \cdot ( a \equiv b \mod m ) \Rightarrow ka \equiv kb \mod b $$
• Due congruenze uguali equivalgono a una potenza. $$ ( a \equiv b \mod m ) \cdot ( a \equiv b \mod m ) \Rightarrow a^2 \equiv b^2 \mod b $$
• Data una congruenza a≡b e un numero intero c qualsiasi valgono le seguenti $$ a+c ≡ b + c \\ ac ≡ bc \\ a^c ≡ b^c $$
• Data una congruenza a≡b mod n e l'intero d è un divisore di n allora a≡b mod d. $$ a≡ b \mod n \:\:, \:\: d|n \Rightarrow a ≡ b \mod d $$

  Esempio. I numeri 15 e 21 sono congruenti modulo 6 $$ 15≡ 21 \mod 6 $$ prendo un divisore 2|6 e verifico se sono congruenti. Sia 15/2 che 21/2 hanno resto 1. Quindi sono anche congruenti modulo 2. $$ 15≡ 21 \mod 2 $$ Lo stesso vale per il divisore 3|6 perché 15/3 e 21/3 hanno entrambi resto 0. Pertanto sono anche congruenti modulo 3. $$ 15≡ 21 \mod 3 $$

• Date due congruenze vale la seguente $$ a≡ b \mod r \:\:, \:\: a≡ b \mod s \Rightarrow a ≡ b \mod \: mcm(r,s) $$
• Date due congruenze vale la seguente $$ ac≡ bc \mod n \Rightarrow a ≡ b \mod \: n/MCD(c,n) $$
• Date due congruenze vale la seguente $$ ac≡ bc \mod n \:\: MCD(c,n)=1 \Rightarrow a ≡ b \mod \: n $$
• Ogni intero a è congruente modulo n a un intero r tale che 0≤r<n $$ a \equiv r \mod n $$

  Dimostrazione. Il resto (r) della divisione a/n non può essere uguale o superiore al divisore n. Se lo fosse, sarebbe ancora divisibile per n e non sarebbe un resto della divisione.

• Dati due interi a,b e un numero primo p, allora vale la congruenza $$ (a+b)^p ≡ a^p+ b^p \mod p $$

Altri esempi pratici

Esempio

Quale numero è congruente a \( 13 \mod 3 \)?

Per trovare il numero congruente a \( 13 \mod 3 \), calcolo il resto della divisione intera tra \( 13 \) e \( 3 \).

$$ 13 \div 3 = 4 \quad \text{con resto } r = 1 $$

Quindi, il resto della divisione è \( 1 \). Questo significa che:

$$ 13 \mod 3 = 1 $$

Pertanto, posso concludere che i numeri \( 1 \) e \( 13 \) sono congruenti modulo 3, perché lasciano lo stesso resto quando divisi per \( 3 \).

$$ 13 \equiv 1 \mod{3} $$

Questo significa che\( 13 \) e \( 1 \) appartengono alla stessa classe di resto modulo \( 3 \). Entrambi lasciano \( 1 \) come resto quando divisi per \( 3 \). 

Esempio 2

Spesso, non è facile calcolare il resto di una divisione.

Ad esempio, in questa congruenza il valore $ 12^{38} $ è molto grande.

$$ 12^{38} \mod{7} $$

In questi casi, per semplificare il calcolo posso utilizzare le proprietà delle potenze e il calcolo delle potenze modulari successive.

• Calcolo $ 12^1 $ $$ 12^1 \mod 7 = 5 $$ Questa congruenza è facile da calcolare perché $ 12 \div 7 = 1 $ con resto $ 5 $
• Calcolo $ 12^2 $ $$ 12^2 \mod 7 = ( 12^1 \cdot 12^1 ) \mod 7 $$ Sapendo che $ 12^1 \equiv 5 \mod 7 $ $$ 12^2 \mod 7 = ( 5 \cdot 5 ) \mod 7 = 25 \mod 7 = 4 $$
• Calcolo $ 12^4 $ $$ 12^4 \mod 7 = ( 12^2 \cdot 12^2 ) \mod 7 $$ Sapendo che $ 12^2 \equiv 4 \mod 7 $ $$ 12^4 \mod 7 = ( 4 \cdot 4 ) \mod 7 = 16 \mod 7 = 2 $$
• Calcolo $ 12^8 $ $$ 12^8 \mod 7 = ( 12^4 \cdot 12^4 ) \mod 7 $$ Sapendo che $ 12^4 \equiv 2 \mod 7 $ $$ 12^8 \mod 7 = ( 2 \cdot 2 ) \mod 7 = 4 \mod 7 = 4 $$
• Calcolo $ 12^{16} $ $$ 12^{16} \mod 7 = ( 12^8 \cdot 12^8 ) \mod 7 $$ Sapendo che $ 12^8 \equiv 4 \mod 7 $ $$ 12^{16} \mod 7 = ( 4 \cdot 4 ) \mod 7 = 16 \mod 7 = 2 $$
• Calcolo $ 12^{32} $ $$ 12^{32} \mod 7 = ( 12^{16} \cdot 12^{16} ) \mod 7 $$ Sapendo che $ 12^{16} \equiv 2 \mod 7 $ $$ 12^{32} \mod 7 =  ( 2 \cdot 2 ) \mod 7 = 4 \mod 7 = 4 $$

A questo punto, grazie alla proprietà delle potenze modulari posso scrivere

$$ 12^{38} = 12^{32} \cdot 12^4 \cdot 12^2 $$

Quindi, riscrivo la congruenza iniziale in questa forma

$$ 12^{38} \mod{7} = (  12^{32} \cdot 12^4 \cdot 12^2 ) \mod{7}  $$

So già che:

• $ 12^{32} \mod 7 = 4 $
• $ 12^{4} \mod 7 = 2 $
• $ 12^{2} \mod 7 = 4 $

Sostituisco i valori nella congruenza.

$$ 12^{38} \mod{7} = (  4 \cdot 2 \cdot 4 ) \mod{7}  $$

$$ 12^{38} \mod{7} = 32 \mod{7}  $$

In questo modo la congruenza $ 32 \mod 7 $ è molto più semplice da calcolare

$$ 32 \div 7 = 4 \quad \text{con resto } r = 4 $$

Quindi, il valore congruente a $ 12^{38} \mod 7 $ è 4

$$ 12^{38} \mod{7} = 4  $$

Esempio 3 (via alternativa)

Un altro modo per risolvere la congruenza con esponente molto grande consiste nell'individuare l'esponente $ x $ che rende $ a^x \equiv 1 \mod m $ ovvero l'ordine di $ a $ modulo $ m $.

Ad esempio, devo risolvere questa congruenza

$$ 12^{38} \mod{7} $$

Per prima cosa mi accorgo che può essere semplificata perché 12 equivale a 5 nel modulo 7.

$$ 12 \equiv 5 \mod 7 $$

Quindi posso sostituire 12 con 5 semplificando i calcoli

$$ 5^{38} \mod{7} $$

A questo punto cerco il minimo $ x $ tale che $ 5^x \equiv 1 \mod 7 $

$$ 5^1 \equiv 5 \mod 7  $$

$$ 5^2 \equiv 25 \equiv 4 \mod 7  $$

$$ 5^3 \equiv 5^1 \cdot 5^2 \equiv 5 \cdot 4 \equiv 20 \equiv 6 \mod 7  $$

$$ 5^4 \equiv 5^2 \cdot 5^2 \equiv 4 \cdot 4 \equiv 16 \equiv 2 \mod 7  $$

$$ 5^5 \equiv 5^3 \cdot 5^2 \equiv 6 \cdot 4 \equiv 24 \equiv 3 \mod 7  $$

$$ 5^6 \equiv 5^3 \cdot 5^3 \equiv 6 \cdot 6 \equiv 36 \equiv 1 \mod 7  $$

L'ordine di 5 modulo 7 è 6, quindi:

$$ 5^6 \equiv 1 \mod 7 $$

Nota. Poiché il modulo 7 è un numero primo e 5 e 7 sono coprimi, in alternativa posso anche usare il piccolo teorema di Fermat $ a^{p-1} \equiv 1 \mod p $ per trovare l'ordine. In questo caso $ p=7 $ e $ a=5 $ $$ 5^{7-1} \equiv 1 \mod 7 $$ $$ 5^{6} \equiv 1 \mod 7 $$ In questo modo ottengo l'informazione molto più rapidamente, senza doverla cercare. Il risultato è lo stesso, l'ordine di 5 modulo 7 è 6.

A questo punto applico la proprietà delle potenze e scompongo l'esponente 38 in funzione dell'ordine 6

$$ 5^{38} \mod 7 $$

$$ (5^6)^6 \cdot 5^2 \mod 7 $$

Sapendo che $ 5^6 \equiv 1 \mod 7 $

$$ (1)^6 \cdot 5^2 \mod 7 $$

$$ 5^2 \mod 7 $$

Ora la congruenza è molto più semplice da calcolare.

$$ 5^2 \equiv 4  \mod 7 $$

Quindi, il risultato è

$$ 12^{38}  \equiv 5^{38} \equiv 4 \mod 7 $$

E' lo stesso risultato ottenuto nell'esempio precedente.

Esempio 4 (teorema cinese dei resti)

Se il modulo è un numero composto si può usare anche il teorema cinese dei resti (CRT).

$$ 2^{85} \mod 91 $$

In questo caso \( 91 = 13 \cdot 7 \) è un numero composto, quindi posso sfruttare la scomposizione di \( 91 \) nei suoi fattori primi e calcolare \( 2^{85} \) modulo 7 e modulo 13 separatamente.

$$ 2^{85} \mod 7 $$

$$ 2^{85} \mod 13 $$

Poi svolgo i calcoli separatamente.

1] Calcolo modulo 7

$$ 2^{83} \mod 7 $$

Poiché 7 è un numero primo e 83 e 7 sono coprimi, posso usare il piccolo teorema di Fermat $ a^{p-1} \equiv 1 \mod p $.

$$ 2^{7-1} \equiv 1 \mod 7 $$

$$ 2^6 \equiv 1 \mod 7 $$

Poiché \( 83 = 6 \cdot 13 + 5 \), scrivo:

$$ 2^{83} \equiv (2^6)^{13} \cdot 2^5 \mod 7  $$

Sapendo che $ 2^6 \equiv 1 \mod 7 $

$$ 2^{83} \equiv 1^{13} \cdot 2^5 \equiv 1 \mod 7 $$

Quindi

$$ 2^{83} \equiv 32 \equiv 4 \mod 7 $$

2] Calcolo modulo 13

$$ 2^{83} \mod 13 $$

Uso di nuovo il piccolo teorema di Fermat $ a^{p-1} \equiv 1 \mod p $ con \( p = 13 \) perché è un numero primo e $ a=2 $ non è multiplo di 13.

$$ 2^{13-1} \equiv 1 \mod 13 $$

$$ 2^{12} \equiv 1 \mod 13 $$

Poiché \( 83 = 12 \cdot 6 + 11 \), scrivo:

$$ 2^{83} \equiv (2^{12})^6 \cdot 2^{11} \equiv 2^7 \mod 13 $$

Sapendo che $ 2^{12} \equiv 1 \mod 13 $

$$ 2^{83} \equiv 1^{12} \cdot 2^{11} \equiv 7 \mod 13 $$

Quindi

$$ 2^{83} \equiv 7 \mod 13 $$

3] Ricostruzione con il teorema cinese dei resti

Posso costruire un sistema con le precedenti congruenze

$$ \begin{cases} x \equiv 4 \mod 7 \\ \\ x \equiv 7 \mod 13 \end{cases} $$

In base alla prima congruenza $ x \equiv 4 \mod 7 $ scrivo \( x \) nella forma:

$$ x = 7k + 4 $$

Sostituisco $ x $ nella seconda congruenza:

$$ 7k + 4 \equiv 7 \mod 13 $$

$$ 7k + 4 - 4 \equiv 7 - 4 \mod 13 $$

$$ 7k \equiv 3 \mod 13 $$

Ora, trovo l'inverso moltiplicativo di \( 7 \) modulo \( 13 \), cioè il numero \( m \) tale che:

$$ 7m \equiv 1 \mod 13 $$

In questo caso è facile trovare che $ m=2 $ perché $ 7 \cdot 2 = 14 \equiv 1 \mod 13 $ ovvero  $ 7^{-1} \equiv 2 \mod 13 $

Nota. In altre situazioni, se il calcolo diventa troppo complesso, posso cercare l'inverso moltiplicativo usando l'algoritmo euclideo esteso.

Ora moltiplico entrambi i lati di \( 7k \equiv 3 \mod 13 \) per \( m=2 \):

$$ 7k \cdot 2 \equiv 3 \cdot 2 \mod 13 $$

$$ k \equiv 6 \mod 13 $$

Quindi, una volta trovato $ k=6 $ lo sostituisco nell'equazione $ x = 7k + 4 $ nel modulo 91

$$ x = 7k + 4 $$

$$ x = 7 \cdot 6 + 4 $$

$$ x = 42 + 4 = 46 \mod 91 $$

Quindi il risultato finale è

$$ 2^{83} \equiv 46 \mod 91 $$ 

E così via.