Identità di Bézout
L'identità di Bézout permette di scrivere il massimo comune divisore di due interi a e b come combinazione lineare a coefficienti interi j e k. $$ MCD(a,b)=d=aj+bk $$
Come trovare i coefficienti dell'identità di Bézout
Per trovare i coefficienti interi j e k posso usare l'algoritmo euclideo delle divisioni successive di un numero.
Un esempio pratico
Devo calcolare il MCD di 2016 e 35
$$ a=2016 \\ b=35 $$
Uso l'algoritmo di Euclide
$$ 2016 = 35 \cdot 57 + 21
\\ 35 = 21 \cdot 1 + 14
\\ 21 = 14 \cdot 1 + 7
\\ 14 = 7 \cdot 2 + 0
$$
Nota. L'ultimo elemento di ogni riga è il resto della divisione.
L'ultimo resto non nullo (7) è il massimo comune divisore dei due numeri
$$ MCD(2016,35)=7 $$
Per trovare i coefficienti dell'identità di Bézout, assegno alle variabili a e b una coppia di valori unitari.
$$ a=(1,0) \\ b=(0,1) $$
Poi scrivo il primo resto delle divisioni successive nella forma
$$ r_1 = a+b(-q_1)
\\ r_2 = b+r_1(-q_2)
\\ r_3 = r_1+r_2(-q_3)
\\ r_4 = r_2+r_3(-q_4)
\vdots $$
Dove $ q_i $ è il quoziente della divisione.
In pratica, dopo aver scritto la prima riga, sposto verso sinistra i componenti senza doverli ricalcolare ogni volta.
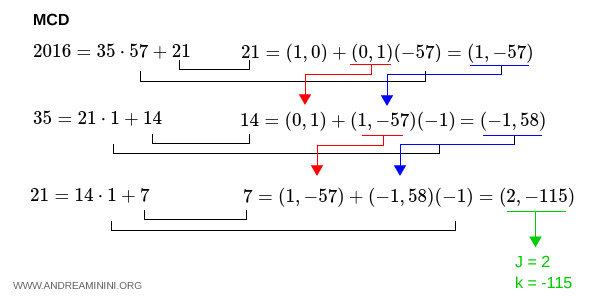
$$ 21 = (1,0)+(0,1)(-57) = (1,0)+(0,-57) = (1,-57) $$
Spiegazione. Nella prima riga del calcolo MCD $$ 2016 = 35 \cdot 57 + 21 $$ il resto è $ r_1 = 21 $, il quoziente è $ q_1 = 57 $. Mentre $ a =(1,0) $ e $ b=(0,1) $.
$$ 14 = (0,1)+(1,-57)(-1) = (0,1)+(-1,57) = (-1,58) $$
$$ 7 = (1,-57)+(-1,58)(-1) = (1,-57) + (1,-58) = (2,-115) $$
Non ci sono altri resti positivi nelle divisioni successive.
L'ultimo risultato sono i coefficienti dell'identità di Bezout.
$$ j=2 \\ k=-115 $$
Quindi posso riscrivere l'identità nella forma
$$ MCD(2016,35)=7=2016 \cdot j + 35 \cdot k $$
$$ 2016 \cdot 2 + 35 \cdot (-115) $$
Ho così trovato il massimo comune divisore nella forma di combinazione lineare di due interi.
Verifica. Svolgo le moltiplicazioni della combinazione lineare per vedere se il risultato è 7. $$ 2016 \cdot 2 + 35 \cdot (-115) \\ 4032 - 4025 = 7 $$
Esempio
Considero i valori
$$ a=1869 \\ b=1617 $$
Utilizzo l'algoritmo di Euclide per trovare il massimo comune divisore $ MCD(1869,1617) $
$$ 1869 = 1617 \cdot 1 + 252
\\ 1617 = 252 \cdot 6 + 105
\\ 252 = 105 \cdot 2 + 42
\\ 42 = 21 \cdot 2 + 0
$$
Quindi, il massimo comune divisore è 21
$ MCD(1869,1617) = 21 $
Ora devo trovare due coefficienti interi $ j $ e $ k $ che soddisfano l'identità
$$ a \cdot j + b \cdot k = MCD(a,b) $$
$$ 1869 \cdot j + 1617 \cdot k = 21 $$
Per trovare i coefficienti $ j $ e $ k $ assegno alle variabili a e b una coppia di valori unitari.
$$ a=(1,0) \\ b=(0,1) $$
Poi scrivo il primo resto delle divisioni successive nella forma $ r_i = r_{i-2} + r_{i-1} \cdot (-q_i) $, considerando $ r_{i-2} = a = (1,0) $ e $ r_{i-1} = b = (0,1) $ nelle prime due righe.
$$ 252 = (1,0) + (0,1) \cdot (-1) = (1, -1) $$
$$ 105 = (0,1 ) + (1,-1) \cdot (-6) = (-6,7) $$
$$ 42 = (1,-1) + (-6,7) \cdot (-2) = (13,-15) $$
$$ 21 = (-6,7) + (13,-15) \cdot (-2) = (-32, 37 ) $$
Quindi, i coefficienti dell'identità sono $ j=-32 $ e $ k=37 $
$$ 1869 \cdot j + 1617 \cdot k = 21 $$
$$ 1869 \cdot (-32) + 1617 \cdot 37 = 21 $$
Verifica. Svolgo i calcoli per verificare se il risultato è corretto. $$ -59808 + 59829 = 21 $$ $$ 21 = 21 $$ L'identità è soddisfatta.
E così via.
