Il prodotto cartesiano delle classi di resto

Due classi di resto Z_r e Z_s sono due anelli rispettivamente modulo r e modulo s, dove r e s sono due interi $$ Z_r, Z_s $$ se i due moduli r e s sono relativamente primi e maggiori di 1$$ MCD(r,s)=1 $$allora anche l'insieme prodotto cartesiano ZrxZs è un anello perché soddisfa le proprietà della somma e del prodotto. $$ (a_r,b_s) + (a'_r,b'_s) = (a_r+a'_r,b_s+b'_s) $$ $$ (a_r,b_s) \cdot (a'_r,b'_s) = (a_r \cdot a'_r,b_s \cdot b'_s) $$

Nelle operazioni si instaura una corrispondenza biunivoca.

Quindi, l'applicazione tra i due insiemi è suriettiva e iniettiva.

A cosa serve? Questa proprietà è particolarmente utile perché mi permette di scomporre e parallelizzare calcoli, altrimenti complessi, affrontandoli separatamente come coppie del prodotto cartesiano. Il risultato finale è sempre lo stesso.

Un esempio pratico

Ho due classi di resto con classi di resto r=3 e s=4

$$ Z_3 = \{ \bar{0}, \bar{1}, \bar{2} \} \\ Z_4 = \{ \bar{0}, \bar{1}, \bar{2}, \bar{3} \} $$

Il prodotto cartesiano è

$$ Z_{3 \cdot 4} = Z_{12} = Z_3 x Z_4 $$

L'insieme del prodotto cartesiano è composto dai seguenti elementi

$$ Z_{12} = Z_3 x Z_4 = \{ \bar{0}_{12} , \bar{1}_{12} , \bar{2}_{12} , \bar{3}_{12} , \bar{4}_{12} , \bar{5}_{12} , \bar{6}_{12} , \bar{7}_{12} , \bar{8}_{12} , \bar{9}_{12} , \bar{10}_{12} , \bar{11}_{12} \} $$

Le coppie del prodotto cartesiano sono:

$$ \bar{0}_{12} = ( \bar{0}_3 , \bar{0}_4 ) \\ \bar{1}_{12} = ( \bar{1}_3 , \bar{1}_4 ) \\ \bar{2}_{12} = ( \bar{2}_3 , \bar{2}_4 ) \\ \bar{3}_{12} = ( \bar{0}_3 , \bar{3}_4 ) \\ \bar{4}_{12} = ( \bar{1}_3 , \bar{0}_4 ) \\ \bar{5}_{12} = ( \bar{2}_3 , \bar{1}_4 ) \\ \bar{6}_{12} = ( \bar{0}_3 , \bar{2}_4 ) \\ \bar{7}_{12} = ( \bar{1}_3 , \bar{3}_4 ) \\ \bar{8}_{12} = ( \bar{2}_3 , \bar{0}_4 ) \\ \bar{9}_{12} = ( \bar{0}_3 , \bar{1}_4 ) \\ \bar{10}_{12} = ( \bar{1}_3 , \bar{2}_4 ) \\ \bar{11}_{12} = ( \bar{2}_3 , \bar{3}_4 ) \\ $$

Attenzione. Nell'elencare le coppie (a,b) occorre seguire una regola. Ripetere s=4 volte le classi di Z₃ = { 0, 1, 2 } nella prima posizione (a). Ripetere r=3 volte le classi di Z₄ = { 0, 1, 2, 3 } nella prima posizione (b). Altri ordinamenti potrebbero non funzionare.

Provo a verificare la proprietà dell'addizione e della somma prendendo due elementi a caso

1] La somma

$$ \bar{3}_{12} + \bar{5}_{12} =\bar{8}_{12} $$

Provo a sommare le rispettive coppie

$$ ( \bar{0}_3 , \bar{3}_4 ) + ( \bar{2}_3 , \bar{1}_4 ) = ( \bar{0}_3 + \bar{2}_3 , \bar{1}_4 + \bar{3}_4 ) = ( \bar{2}_3 , \bar{0}_4 ) $$

La somma delle coppie è uguale alla coppia Z₈.

$$ \bar{8}_{12} = ( \bar{2}_3 , \bar{0}_4 ) $$

La corrispondenza biunivoca della somma è soddisfatta.

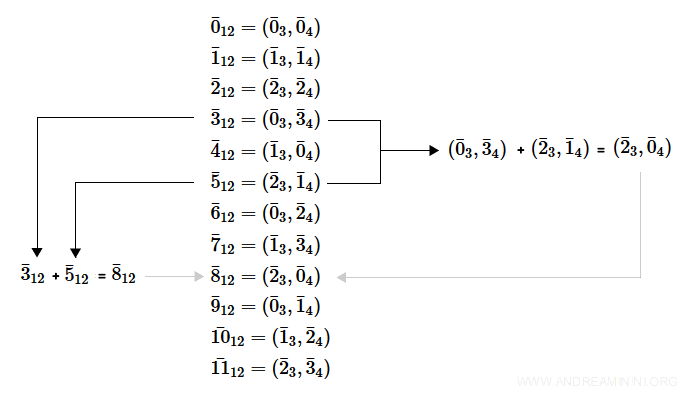
1] La moltiplicazione

$$ \bar{3}_{12} \cdot \bar{5}_{12} =\bar{15}_{12} = \bar{3}_{12} $$

Nota. Il prodotto 3·5=15₁₂ è congruente modulo 12 con la classe 3₁₂. perché la divisione 15/12 ha resto 3.

Provo a moltiplicare le rispettive coppie

$$ ( \bar{0}_3 , \bar{3}_4 ) \cdot ( \bar{2}_3 , \bar{1}_4 ) = ( \bar{0}_3 \cdot \bar{2}_3 , \bar{3}_4 \cdot \bar{1}_4 ) = ( \bar{0}_3 , \bar{3}_4 ) $$

Il prodotto delle coppie è uguale alla coppia Z₃.

$$ \bar{3}_{12} = ( \bar{0}_3 , \bar{3}_4 ) $$

La corrispondenza biunivoca del prodotto è soddisfatta

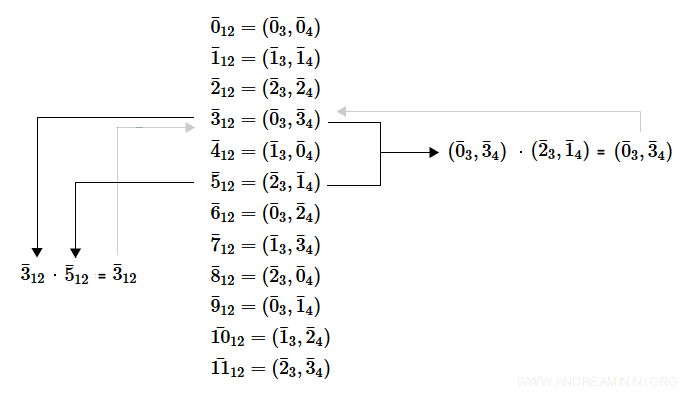
Nota. Questo esempio è molto semplice. Ha il solo scopo di far comprendere la corrispondenza biunivoca. La vera potenza della corrispondenza biunivoca si apprezza in particolar modo quando l'operazione da svolgere è molto complessa.

E così via.